Światło bywa spolaryzowane. Foton to kwant światła. Może występować w dwóch polaryzacjach kołowych. Dla fotonów jednak mówimy raczej o skrętności. Pisał o tym przed dwoma laty św. pamięci bloger Eine w notce "Wśród tajemnic światła (5) Helikalność i chiralność fotonów". I ja teraz o tym piszę. Lubię tajemnice. Czasem należy je ujawniać. Czasem nie należy. Skrętność fotonów można bez szkody ujawnić. Tym bardziej, że pod ostatnią notką zapytał o to niestrudzony w swych dociekaniach internauta Bjab. Jednak by do usłyszenia tajemnic dojrzeć, trzeba przestać się bać macierzy. Licealiści się wciąż macierzy boją. Podobnie jak ich nauczyciele. Bjab się macierzy nie boi i stąd ta notka - wynika z konieczności udzielania odpowiedzi na ważne pytania.
Pojawiła się więc w poprzedniej notce macierz-operator skrętności Λ:
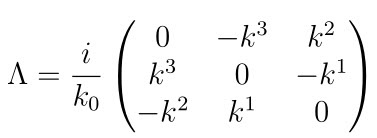
gdzie k0 = √ ((k1)2+(k2)2+(k3)2)=√ k2.
k=(k1,k2,k3) to wektor falowy, ściśle związany z pędem p=ℏk.
Za k1,k2,k3 można wstawić dowolne konkretne trzy liczby rzeczywiste. Byle nie wszystkie trzy naraz równe zeru. Można też operować na ogólnych symbolach, na zmiennych k1,k2,k3.
Macierz Λ jest hermitowska - równa swej transponowanej i zespolenie sprzężonej. Transponowanie w tym przypadku sprowadza się do zastąpienia k przez -k. Sprzężenie zespolone sprowadza się w tym przypadku do zamiany i na -i.
Macierze hermitowskie mają rzeczywiste wartości własne. Fizycy liczby rzeczywiste bardzo lubią. Mówią: to możliwe wyniki pomiarów. Pomiary zawsze prowadzą do liczb rzeczywistych. Macierze hermitowskie w teorii kwantów reprezentują "obserwable" - wielkości, które możemy "obserwować" lub "mierzyć".
Macierz Λ ma trzy różne wartości własne. Licealiści powinni się uczyć jak je wyliczać. W naszym przypadku Λ ma trzy różne wartości własne: 0, -1, +1. Gdy zmierzymy 0 - to nie jest foton. Foton to albo -1 (foton o polaryzacji kołowej lewo-skrętny), albo +1 (foton o polaryzacji kołowej prawo-skrętny). Co nie oznacza, że innych fotonów nie ma. Ale o tym dalej.
Do operacji na macierzach przydają się programy komputerowe. To znaczy dobrze jest umieć operować na macierzach na kartce papieru. Ale lepiej użyć programu. Ja lubię program Mathematica. W wersji darmowej występuje jako Wolfram Alpha. Jest też całkowicie darmowy, o potężnych mozliwościach obliczeniowych, program Reduce. Czego to on nie potrafi!
Przy użyciu jednego z takich programów z łatwością wyliczamy kwadrat macierzy Λ (Kleopatra intensywnie używała obydwu programów robiąc obliczenia do naszej pracy o operatorze położenia dla fotonu). Oznaczymy go literką P. P=Λ2. Dlaczego literka P? O tym za chwilę.
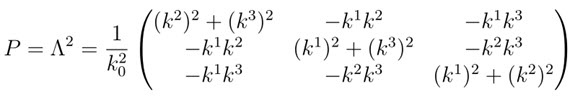
Macierz P jest rzeczywista i symetryczna. Jest zatem hermitowska, P=P*, i może reprezentować wielkość fizyczną. Ale jaką?
Możemy bez trudu podnieść macierz P do kwadratu i przekonać się, że
P2= P.
Mówimy, że P jest idempotentem. Jej (tej macierzy P) wartości własne spełniają to samo równanie co sama macierz. Jeśli p jest wartością własną macierzy P, to p jest liczbą rzeczywistą i p2=p. Są tylko dwa rozwiązania tego prostego równania algebraicznego: p=0 lub p=1. Zero i jeden to wartości logiczne "nie" i "tak". Fałsz i prawda. Macierz P reprezentuje pytanie fizyczne. Odpowiedź na to pytanie to "nie" lub "tak". A co to za pytanie?
P: Czy jesteś fotonem?
Odpowiedź może brzmieć: nie, nie jestem lub tak, jestem. Jeśli nie jesteś, idź sobie gdzie indziej, nie zawracaj głowy. Jeśli jesteś fotonem, jesteś przedmiotem tej notki. Będziemy teraz dalej pytać: o twoją skrętność.
P to taki filtr. Odfiltrowuje fotony. Plewy niefotonowe odrzuca. Lub inaczej to projektor. Stąd i literka P. To projektor na podprzestrzeń stanów fotonowych. Stany o skrętności zero odrzuca. Zeruje się na nich.
Podnieśliśmy Λ do potęgi drugiej. Czemu nie do trzeciej? Na kartce papieru z ołówkiem to nie na głowę licealisty. Kiedyś ludzie to potrafili, ale dziś nasze głowy są zbyt leniwe. Pozostaje program komputerowy. Chyba, że ktoś programów nie lubi. Wtedy nauczy się, że każda macierz hermitowska daje się zdiagonalizować, że gdy zdiagonalizujemy Λ, to zdiagonalizujemy tym samym każdą tej Λ potęgę, i wtedy wszystko stanie się natychmiastowe i oczywiste. Bez tego zostają programy. I program nam natychmiast wylicza, że
Λ3 = Λ.
Inaczej:
ΛP=PΛ=Λ
Co za niespodzianka. Reszta to już łatwa zabawa w algberę. Z górki na pazurki. Definiujemy jak w poprzedniej notce:
P1 = (Λ2+Λ )/2
P2 = (Λ2-Λ )/2
Teraz P1 i P2 są projektorami-pytaniami. Mamy
P12=P1,
P22=P2,
P1P2=P2P1=0,
P1+P2=P
Te pytania, wraz z pytaniem 0 na które odpowiedź jest zawsze "nie" oraz z pytaniem 1, na które odpowiedź jest zawsze "tak", tworzą logikę kwantową. W istocie jest to logika klasyczna, bowiem wszystkie te projektory ze soba komutują. Jednak działają w przestrzeni stanów kwantowych.
P1 to pytanie: czy masz skrętność +1?
P2 to pytanie: czy masz skrętność -1?
Leci foton i zadajemy pytanie P1. Odpowiedź brzmi tak lub nie. 1 lub 0. Jednak foton nie musi mówić przy tym prawdy. Zadanie pytania wymusza na nim odpowiedź. Chciałby może odpowiedzieć: ani +1 ani -1, jestem superpozycją. Jednak pomiar wymusza tak lub nie. No i biedny foton jest zmuszony do wykonania "skoku kwantowego". Rzuca sobie monetą i zależnie od tego co mu wypadnie wybiera odpowiedź tak lub nie. I zapomina czym był przedtem. Einstein mówił "Bóg nie gra w kości". W coś tam jednak gra, i póki co fotony zachowują się tak jakby grały. Wymuszamy na nich dwuwartościową logikę, która jest im obca.
Dodatek: konstrukcja operatora rzutowego P1(k) przy pomocy wektora e(k). Bjab napisał
Spostrzeżenie:
Pierwsza kolumna macierzy P1 bardzo przypomina obliczony wektor e(k) z notki:
https://www.salon24.pl/u/arkadiusz-jadczyk/1222369,wektor-riemanna-sielbersteina-z-przedzialkiem-z-boku-przestaje-straszyc
Bierzemy wektor e(k) ze wspomnianej notki
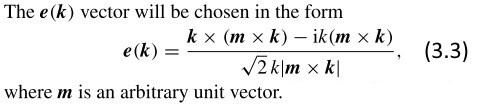
Jednak lepiej zapisywać go jak e(m,k) by uwydatnić zależność od m.
W notacji Diraca bra i ketów zapiszemy ten wektor jako ket |e(m,k)). W notacji Diraca uzywamy dzióbków. Jednak edytor salonowy na dzióbki czasem brzydko reaguje. Mamy również sprzężny do niego bra (e(m,k)|. Mnożymy ket przez bra i dostajemy operator rzutowy
Q1(m,k) = |e(m,k)) (e(m,k)|.
Co ten operator robi działając na f? Bierze iloczyn skalarny e(m,k) i f. i mnoży przez tę liczbę wektor e(m,k).
Q1(m,k) |f) = |e(m,k))(e( m,k)|f)=(e(m,k)|f) |e(m,k))
Wynikiem jest wektor proporcjonalny do e(m,k). Jest reprezentowany przez macierz. Tę macierz możemy wyliczyć. Wektor ket |e(m,k)) jest kolumienką - jak wyżej. Wektor bra (e(m,k)| jest wierszem. Elementy tego wiersza to liczby zespolenie sprzężone do elementów kolumienki |e(m,k)) . Jednak widać, że sprzężenie zespolone jest w tym przypadku równoważne zastąpieniu k przez -k. Możemy użyć programu Mathematica by obliczyć macierz Q1(m,k) zdefiniowaną powyżej. Do tego celu użyjemy komendy KroneckerProduct. Mnoży kolumnę przez wiersz. Wychodzi macierz 3x3.
Oto odpowiedni kod programu Mathematica
Bierzemy wektor e (k) z formuły (3.3) od Białynickiego. Najpierw definicja sprzężenia zespolonego
bar[x_] := Simplify[ComplexExpand[x]/.{I -> -I, -I-> I}]
k0=Sqrt[k.k];
k={k1,k2,k3};
m={m1,m2,m3};
Mianownik formuły (3.3)
mk2=Sqrt[2]*k0*Sqrt[Simplify[Cross[m,k].Cross[m,k]]];
Out[56]= Sqrt[2] Sqrt[k1^2+k2^2+k3^2] Sqrt[(k2 m1-k1 m2)^2+(k3 m1-k1 m3)^2+(k3 m2-k2 m3)^2]
Wektor e (m,k) z formuły (3.3)
In[62]:= e1=ComplexExpand[Simplify[Cross[k,Cross[m,k]]-I*k0*Cross[m,k]]]/mk2;
e1b=bar[e1];
Operator rzutowy P1 przepisany z poprzedniego BB3.nb
P1={{(k2^2+k3^2)/(2 (k1^2+k2^2+k3^2)),((k2 k3-I k1 Sqrt[k1^2+k2^2+k3^2]) (k1 k3-I k2 Sqrt[k1^2+k2^2+k3^2]))/(2 (k1^2+k2^2) (k1^2+k2^2+k3^2)),(I (I k1 k3+k2 Sqrt[k1^2+k2^2+k3^2]))/(2 (k1^2+k2^2+k3^2))},{((k2 k3+I k1 Sqrt[k1^2+k2^2+k3^2]) (k1 k3+I k2 Sqrt[k1^2+k2^2+k3^2]))/(2 (k1^2+k2^2) (k1^2+k2^2+k3^2)),(k1^2+k3^2)/(2 (k1^2+k2^2+k3^2)),-((k2 k3+I k1 Sqrt[k1^2+k2^2+k3^2])/(2 (k1^2+k2^2+k3^2)))},{-((k1 k3+I k2 Sqrt[k1^2+k2^2+k3^2])/(2 (k1^2+k2^2+k3^2))),(I (I k2 k3+k1 Sqrt[k1^2+k2^2+k3^2]))/(2 (k1^2+k2^2+k3^2)),(k1^2+k2^2)/(2 (k1^2+k2^2+k3^2))}};
Sprawdzamy, że ma helicity + 1
FullSimplify[P1.e1-e1]
Out[58]= {0,0,0}
Sprawdzamy, że ma normę 1
In[64]:= Simplify[e1b.e1]
Out[64]= 1
Definiujemy operator Q1 jak w BB3.nb ale z użyciem wektora e1 tego powyżej
In[69]:= Q1=FullSimplify[KroneckerProduct[e1,e1b]]
Out[69]= {{(k2^2+k3^2)/(2 (k1^2+k2^2+k3^2)),-((k1 k2+I k3 Sqrt[k1^2+k2^2+k3^2])/(2 (k1^2+k2^2+k3^2))),(I (I k1 k3+k2 Sqrt[k1^2+k2^2+k3^2]))/(2 (k1^2+k2^2+k3^2))},{(-k1 k2+I k3 Sqrt[k1^2+k2^2+k3^2])/(2 (k1^2+k2^2+k3^2)),(k1^2+k3^2)/(2 (k1^2+k2^2+k3^2)),-((k2 k3+I k1 Sqrt[k1^2+k2^2+k3^2])/(2 (k1^2+k2^2+k3^2)))},{-((k1 k3+I k2 Sqrt[k1^2+k2^2+k3^2])/(2 (k1^2+k2^2+k3^2))),(I (I k2 k3+k1 Sqrt[k1^2+k2^2+k3^2]))/(2 (k1^2+k2^2+k3^2)),(k1^2+k2^2)/(2 (k1^2+k2^2+k3^2))}}
In[70]:= Simplify[P1-Q1]
Out[70]= {{0,0,0},{0,0,0},{0,0,0}}
Z czego wynika, że pierwsza kolumna macierzy P1 to iloczyny kolejnych składowych wektora e(m,k) przez pierwszą składową wektora e(m,-k).
Zgodnie z obserwacją Bjaba mamy Q(m,k)=Q(m',k)=P1(k) dla dowolnych jednostkowych m,m' i dla dowolnego k.










Komentarze