Nowe podejście do rozumienia wymiaru kołowego czyli zbliżenie geometrii z fizyką.
Używać będę czasem pojęcia „kwantowania” lub „skwantowania” obiektu. Co to znaczy? Kwantowanie zachodzi w momencie międzywymiarowego przejścia obiektu, ponieważ obiekt czterowymiarowy może być postrzegany – obserwowany jako trój-, dwu- i jedno wymiarowy, w zależności od sposobu obserwacji i użytej metody badawczej. Na przykład dualizm korpuskularno falowy wynika z wymiarowego zróżnicowania obserwacji tego samego meta-obiektu, który raz postrzegany może być jako cząstka punktowa, a innym razem jako przestrzenna fala (raz podłużna, raz poprzeczna) czyli w pierwszym i drugim przypadku stosowane są inne metody badawcze narzucające obserwacje różnych stanów oraz części jednego meta-obiektu
Chodzi o to, że jedną i tę samą cząstkę (meta-cząstkę) możemy postrzegać na różne sposoby i uważając je za rózne cząstki nazywamy różnymi cząstkami! A to są po prostu różne stany jednej i tej samej meta-cząstki!
Postaram się wykazać i udowodnić, że Meta-fizyka to żadne czary mary, lecz świadomość istnienia obiektów i zdarzeń, które znajdują się i zachodzą w wyższej wymiarowości czyli w Metaprzestrzeni
Metaprzestrzeń, to przestrzeń tak zwanej próżni. Z przestrzeni próżni wyłaniają się zaś zróżnicowane cząstki, które są róznymi stanami jednej i tej samej "mega-cząstki". I obszar, w którym ta jedna cząstka jest obserwowana jako wiele róznych cząstek to przestrzeń 3D euklidesowa, w której przejawia się "nasz świat fizyczny". To przestrzeń, w której pojawia się także wymiar czasu i staje się ona wtedy czasoprzestrzenią 4D.
Gdy myślę o przestrzeni jako wypełnionej cząstkami wirtualnymi - eterem, wówczas jest ona próżnią. W próżni znajdują się idee wszystkich potencjalnych stanów jednej i tej samej meta-cząstki. Takiej przestrzeni próżni przypisuję wartość wielości "n". W przestrzeni próżni istnieją wszystkie potencjalne czyli wirtualne stany jednej meta-cząstki. To też przestrzeń bezczasowa. W metaprzestrzeni każda cząstka może stac się meta cząstką, gdy jej wartość zostanie ubezwzględniona i przyrównana do jedności
Proponowana przeze mnie metoda pozwala na dokonywanie w naszym płaskim świecie obserwacji Metaprzestrzeni. W konsekwencji "nowa geometria" kwantowa, model Grawitora oraz dalsze rozważania mogą prowadzić do unifikacji teorii grawitacji kwantowej i klasycznej, Pętlowej Grawitacji z Teorią Strun, z STW, z OTW i innymi, a także do pogodzenia ich wszystkich, z koniecznością weryfikacji w ramach zrozumienia prawdziwej natury grawitacji i czaso-przestrzeni.
Wymiar kołowy
Cząstka punktowa, tak samo jak geometryczny punkt, może być obserwowana "na dwuwymiarowej płaszczyźnie euklidesowej" jako przesunięcie punktu względem dwóch współrzędnych (wymiarów) x oraz y.

Z funkcji trygonometrycznej wynika, że dla każdego okręgu r² = x²+ y². Przyjmijmy, że r jest równe 1. Sporządzeniu WYKRESU danej funkcji „fizycznie” odpowiada:
a) przesunięcie pojedyńczego punktu geometrycznego względem dwóch współrzędnych x i y po okręgu (równe jednemu cyklowi)
i/albo
b) jednoczesne przedstawienie wszystkich punktów geometrycznych składających się na wykres funkcji jako okręgu o promieniu r =1 i wzorze L= 2 π r
W ten sposób geometryczny punkt na dwuwymiarowej płaszczyźnie może stać się okręgiem, jeśli zostanie wprowadzony w ruch. Punkt zostaje wtedy „wprawiony w ruch”, któremu odpowiada wykres funkcji przedstawiany jako okrąg równy orbicie punktu geometrycznego Możemy także ten ruch cząstki przedstawic jako okrag czyli superpozycję punktu (cząstki punktowej) w wymiarze kołowym. Teraz możemy przedstawić zbiór punktów jako L = 2 π r. Oto wykres funkcji możemy zastąpić okręgiem czyli piątym wymiarem – kołowym.
Ujęcie fizyczne – kwantowanie okręgu
Punkt geometryczny nie porusza się sam, a wykres funkcji jest rodzajem ruchu wykonanego przez pojedyńczy punkt w celu zapisania jego ruchu stanowiącego okrąg. Nazwałam ten okrąg „orbitą” punktu. Można zatem powiedzieć, że okrąg to inaczej ruch geometrycznego punktu na geometrycznie wyznaczonej „orbicie” równej 2 π r. Z drugiej strony można też powiedzieć, że na okrąg składają się wszystkie punkty geometryczne konieczne do opisania tego okręgu. Wszystkie punkty odpowiadają wówczas superpozycji jednego punktu – jednej cząstki punktowej na jej „orbicie”. Superpozycja odpowiada wówczas „rozmyciu” cząstki na swojej orbicie
W takiej sytuacji fizycznie wszystkie punkty tworzące okrąg wyznaczają orbitę jednego punktu. Superpozycja punktu na okręgu odpowiadałyby wszystkim miejscom położenia punktu w jego polu grawitacyjnym - na całej jego orbicie. Możemy to zapisac przy pomocy wymiaru kołowego. Gdy do tego dodamy wymiar czasu, obwód okręgu stanowiącego orbitę punktu wyznaczałby określoną prędkość stałą punktu geometrycznego - cząstki punktowej.
Wymiar kołowy Kaluzy – Kleina został przyjęty w Teorii Strun za wymiar prawie tak samo równoprawny, jak dotychczas znane nam cztery wymiary (3 proste przestrzenne oraz wymiar czasu). Rozumie się przez to tyle, że do każdego punktu materialnego – cząstki punktowej w wyższej wymiarowości, w wymiarze kołowym dołączony jest okrąg lub raczej każdy punkt materialny – cząstka punktowa znajduje się na okręgu, z tym jednak ograniczeniem, że wielkość takiego okręgu jest bardzo mała i nie może przekraczać progu Plancka. Z drugiej strony w Teorii Strun istnieją struny i brany o ogromnych wielkościach. Dlatego moja propozycja wymaga rezygnacji z dotychczasowego ograniczenia „wielkości” wymiaru krzywizny do progu Plancka, a przyjęcia, że wymiar kołowy nie ma przestrzennego ograniczenia. Stąd wynika pierwsza teza wymiaru kołowego.
TEZA I
1. Do każdego punktu materialnego – cząstki punktowej dołączony jest okrąg lub raczej każdy punkt materialny – cząstka punktowa znajduje się na okręgu, którego wielkość może być dowolna i jest zależna jedynie od stanu danego okręgu.
2. Każdy punkt w dodatkowym wymiarze – wymiarze kołowym znajduje się na okręgu.
3. Każdy odcinek prostej może stać się okręgiem, jeśli zostanie skwantowany czyli przeniesiony do dodatkowego wymiaru kołowego. Analogicznie każdy okrąg może stać się odcinkiem prostej, jeśli zostanie skwantowany i wyprowadzony z wymiaru kołowego do wymiarów prostych.
4. W wymiarze kołowym zmiennymi są obwód L okręgu (koła) oraz jego promień. Stałą jest wyłącznie liczba "Pi".
Okrąg, w którym wartość jednego z promieni w wymiarze x lub y zbliży się do zera, może utworzyć prostą (odcinek prostej). Będzie to zmiana wymiarowa – okrąg ulegnie wówczas skwantowaniu z dwóch wymiarów prostych do jednego: x lub y.
5. Każdy okrąg może być 1D sferą, a to znaczy, że każdy punkt może w przestrzeni trójwymiarowej znajdować się także na sferze.
Oto na płaszczyźnie euklidesowej obserwujemy okrąg o geometrii L = 2 π r, gdzie r = 1. Zgodnie ze wzorem na okrąg L = 2 π r wiemy, że odcinek „r” został „zakrzywiony” przez wielkość „2 π” do postaci okręgu albo odcinek „2r” został „zakrzywiony” przez wielkość „π” do postaci okręgu. W takim przypadku łatwo zaobserwować, że inna jest krzywizna zerowa euklidesowej płaszczyzny odniesienia reprezentowana przez odcinek prosty L = 2r niż krzywizna samego okręgu L = π 2r. W zasadzie moglibyśmy z powodzeniem stwierdzić, że na przykład odcinek wielkości L = 2r jest specyficzną postacią – stanem okręgu. Specyficzną dlatego, że jest to okrąg „przeniesiony” z wymiaru kołowego do stanu odcinka prostej L = 2r. Takie „przeniesienie” proponuję nazwać „kwantowaniem w metryce". Wartość π jest ustalona jako stała, a wartości obwodu L i promienia r są zmiennymi w wymiarze kołowym. Powoduje to, że okrąg w postaci L = 2r staje się jednowymiarowy. Natomiast odcinek prostej L = 2r może zostać „przeniesiony” do innej wymiarowości, w tym wypadku do wymiaru kołowego, do postaci L = π 2r, a wtedy staje się okręgiem czyli odcinkiem prostej, który osiągnął swój nowy stan wymiarowy. Istnieje jeszcze inny sposób kwantowania okręgu wymagający przenoszenia go z wymiaru kołowego do wymiaru krzywizny, co postaram się wyjaśnić w dalszej części.
Nowe podejście do rozumienia pojęcia krzywizny oraz wprowadzenie nowego wymiaru krzywizny.
Pojęcie krzywizny zostało wprowadzone przez Georga Bernharda Riemanna i rozwinięte przez Hermana Minkowskiego. Nie mam zamiaru podważać ich osiągnięć. Chciałabym jednak przedstawić i rozważyć nowe ujęcie problemu krzywizny figur - obiektów dla potrzeb nowej geometrii kwantowej. Bohaterem rozważań, które mogą nas zbliżyć do grawitacji kwantowej jest okrąg.
Dotychczasowo obowiązujący pogląd mówi nam, że zmiana krzywizny przestrzeni zachodzi w ten sposób, że na przykład okrąg o geometrii L = π 2r znajdujący się na płaszczyźnie o krzywiźnie zerowej przeniesiony na powierzchnię kuli zmienia swoją krzywiznę, ponieważ to płaszczyzna kuli charakteryzuje sie krzywizną dodatnią. (czy to nie jest masło maślane?). Zmiana ta zachodzi poprzez wytyczenie nowej, nieeuklidesowej płaszczyzny odniesienia w ten sposób, że obwód okręgu „L” oraz promień „r” pozostają bez zmian, ale są umiejscowione na powierzchni kuli lub tak zwanej powierzchni „siodła”. W ten sposób niezaprzeczalnie zmianie ulega przestrzenna wymiarowość samego okręgu, ale jest zależna – określana poprzez inną płaszczyznę odniesienia – sferyczną płaszczyznę kuli. Okrąg wraz ze swoim promieniem jest „opisany” na powierzchni kuli czyli na sferze. Rysunek nr 2
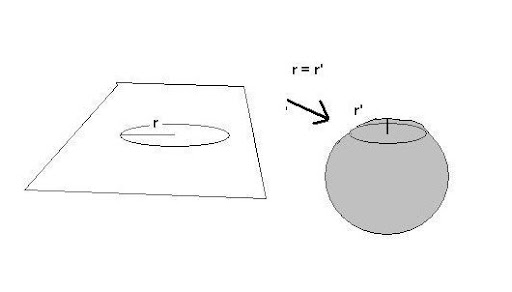
Czy jednak do określenia zmiennej krzywizny obiektu konieczna jest płaszczyzna odniesienia o zróżnicowanych krzywiznach? Wystarczy wyobrazić sobie choćby gumkę aptekarską (nie tyle ze względu na jej sprężystość, ile na fakt utrzymywania „okrągłości” przy odkształcaniu),. Taką gumkę - okrąg możemy odkształcać i skręcać na przykład do postaci dwóch okręgów, a potem obserwować przestrzenne zmiany jej kształtu na płaszczyźnie euklidesowej. Rys. 3 i 4
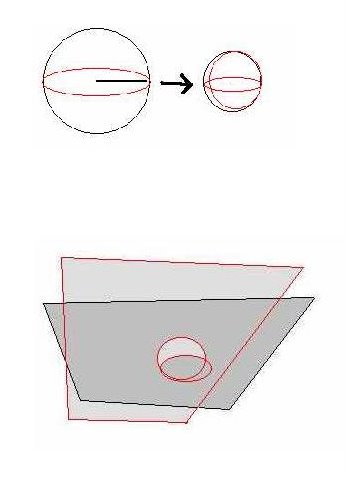
Czy możliwe jest zaobserwowanie zmiennej krzywizny takiego „obiektu” przy użyciu euklidesowejpłaszczyzny odniesienia ? Proponuję potraktować okrąg nie jako figurę, lecz jako obiekt fizycznyi poszukać sposobu obserwacji zmian krzywizny takiego obiektu na płaszczyźnie euklidesowej. W tym przypadku nie używamy metody wymagającej kombinacji z przenoszeniem okręgu na powierzchnię kuli lub siodła. Potrzebna jest metoda pozwalająca zaobserwować to, w jaki sposób przestrzenne odkształcenie okręgu mogłoby być obserwowalne na euklidesowej płaszczyźnie odniesienia. Taka nowa metoda istnieje, lecz wymaga przyjęcia zasady zmienności stanów okręgu, co by znaczyło, iż istnieje jakiś jeden meta-okrąg, który może zostać przestrzennie tak odkształcony, że zmienia on swoją krzywiznę na dodatnią lub ujemną czyli może znajdować się w różnych stanach w wyższych wymiarach, poza euklidesową płaszczyzną odniesienia. Na płaszczyźnie euklidesowej obserwowalibyśmy wtedy różne okręgi (o różnym promieniu i obwodzie) jako różne stany jednego meta-okręgu, a każdy okrąg na płaszczyźnie euklidesowej byłby jedynie czymś w rodzaju rzutu lub cienia - stanu wielowymiarowego meta-okręgu.
Zasadę zmienności stanów okręgu określa kolejna teza.
TEZA II
1. Każdy okrąg znajduje się w stanie o zerowej krzywiźnie tylko wtedy, gdy występuje jako o d c i n e k prostej (2r). Zaś odcinek prostej może zostać skwantowany czyli przeniesiony do wymiaru kołowego do postaci okręgu o wzorze L = π 2r. Ten proces kwantowania czyli przeniesienia odcinka prostej do innej wymiarowości jest opisany przez użycie liczby „π ” we wzorze L = π 2r.
2. Każdy okrąg może znajdować się w stanie o krzywiźnie dodatniej lub ujemnej, gdy zostaje skwantowany czyli przeniesiony do wymiaru krzywizny.
3. Każdy okrąg o różnym promieniu i różnym obwodzie może być róznym stanem jednego meta-okręgu znajdującego się w Meta- przestrzeni.
Aby udowodnić tę tezę należy znaleźć możliwość przedstawiania na płaszczyźnie euklidesowej różnych stanów meta-okręgu jako różnych okręgów o zmiennej krzywiźnie. Poniżej przedstawiam taki sposób. Na pierwszym rysunku mamy okrąg L = π 2r, gdzie r = 1. Ten okrąg znajduje się w stanie A. Następnie okrąg przechodzi do innego stanu, który może być obserwowany na powierzchni kuli o innej krzywiznie niż płaszczyzna euklidesowa. Rys.5
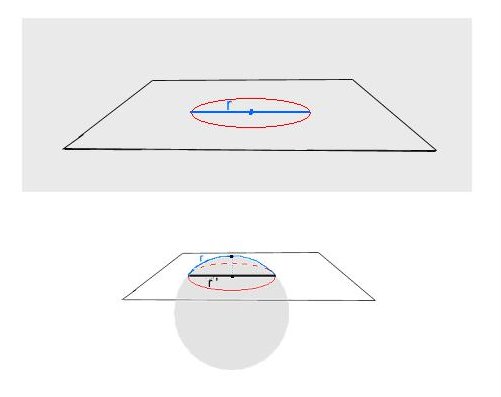
Krzywizna płaszczyzny odniesienia w przypadku powierzchni kuli i płaszczyzny euklidesowej jest oczywiście różna: powierzchnia kuli jest dodatnia, więc obwód i promień w zasadzie nie ulega żadnej zmianie prócz tej, że promień r’ przechodzi do dodatkowego wymiaru "z". Rys.6
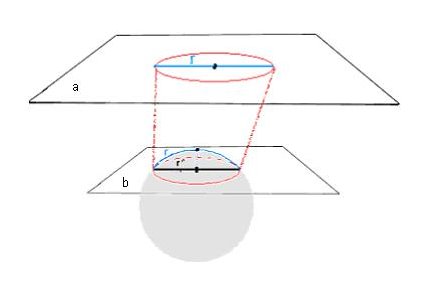
Realny promień okręgu (niebieski) „pozostaje” poza płaszczyzną euklidesową b. czyli w dodatkowym wymiarze "z". Dlatego obserwujemy, że obwód maleje wraz z promieniem, a to tylko zmienia się krzywizna. Tak, jak na rysunku poniżej. Rys.7
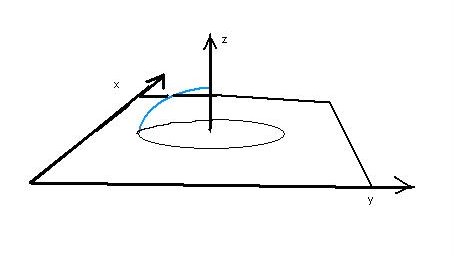
W dotychczasowej interpretacji naukowcy „gubią” gdzieś wielkość obwodu tłumacząc, że zmiana obwodu jest „równoważona” przez zmianę krzywizny. Nie otrzymujemy jednak odpowiedzi na pytania: Dlaczego tak się dzieje, że wydaje nam się, że obwód okręgu na płaszczyźnie kuli jest mniejszy, skoro został tylko przeniesiony na płaszczyznę kuli? I co naprawdę dzieję się z obwodem? Uległ odkształceniu, podobnie jak promień, ale co to za odkształcenie?
Tego typu przetworzenie wyjaśnia się na przykład w OTW w następujący sposób:”(...) koło na powierzchni kuli ma mniejszy obwód niż koło wykreślone na kartce papieru (powierzchni euklidesowej). A większy będzie miało narysowany na powierzchni siodła. (…) Takie skrócenie obwodu to nic innego jak skrócenie Lorentza." (- Brian Greene „Piękno wszechświata”.) W OTW, kiedy mamy do czynienia z ruchem przyśpieszonym – przykład z Chudym i Rudym na karuzeli, tłumaczy się, że im większa jest odległość od środka koła Chudego mierzącego długość promienia, tym Rudy będzie obserwował na obwodzie (mierzył linijką ) coraz większe przyśpieszenie. Obwód przyjęto za zmienny, a promień za stały. Dlaczego obwód nie ulega takiemu samemu skróceniu jak linijka? Skrócenie Lorentza obwodu karuzeli ma znaczenie tylko wtedy, gdybyśmy porównywali właściwości karuzeli znajdującej się w ruchu i w spoczynku. W podanym przykładzie nie jest to uwzględniane ani podobno potrzebne. Przyjmijmy jednak na początek założenie zgodne z dokonywaną obserwacją na płaszczyźnie euklidesowej, że zmniejszenie obwodu następuje jednocześnie wraz ze "skróceniem", które jest wynikiem odkształcenia obwodu - okręgu oraz promienia w wymiarze krzywizny.
W podanych przeze mnie przykładach widać wyraźnie, że przy tego typu przekształceniach promień obserwowany na płaszczyźnie euklidesowej ulega skróceniu. Jest to wynik „łamania” promienia na pod-promienie czyli na „wektory”. A „łamanie to następuje z powodu ‘skręcania” okręgu. Skracanie promienia jest odwrotnie proporcjonalne do coraz większej ilości pod-promieni (wektorów).
ciąg dalszy prawdopodobnie nastapi... pt.:
Fizyczne właściwości okręgu a jego geometria obserwowana w wymiarze krzywizny.

