Pokonać swoje słabości i zwyciężyć sam siebie. Znaleźć czas i zapał aby dokończyć wbrew wszystkiemu i wszystkim, coś co wszyscy uważali za niemożliwe i przy tym nie zwariować.
Tekst jest długi ale rozbijanie go na kilka części powoduje że czytelnik jest zagubiony. Tutaj przedstawiłem pełną odpowiedź jedynie na schemat pierwszy, ale po kilku dniach pisania, liczenia sprawdzania mam już troche dość (za dużo na raz). Wiem że nie wszystko jest tak jakby sobie tego inni życzyli, są uproszczenia, nie wszystko jest poparte dowodem i źródłami, niektóre kalkulacje są na liczbach nie na zmiennych, ale gdybym chciał to zrobić tak jak powinno to wyglądać, to nie wiem czy udało by mi się osiągnąć chociaż połowę tego co już osiągnąłem. Konkluzje i wnioski tu opisane nie są jedynie moimi wymysłami, a są one oparte na wieloletniej mojej pracy, setek wyliczeń i poprawiania setek błędów. Często za jakimś prostym stwierdzeniem kryje się mnóstwo pracy jaką musiałem wykonać by te stwierdzenie potwierdzić.
Całość nie jest łatwa do ogarnięcia (mi zajęło to ponad dwa lata) i zawiera dużą ilość detali z których każdy jest ważny. Niestety notka będzie trudna do zrozumienia dla tych którzy nie posiadają wiedzy z Fizyki co najmniej na poziomie maturalnym.
Pytanie jest jak działają siły więzów podczas obrotu ciała sztywnego? mamy trzy sytuacje.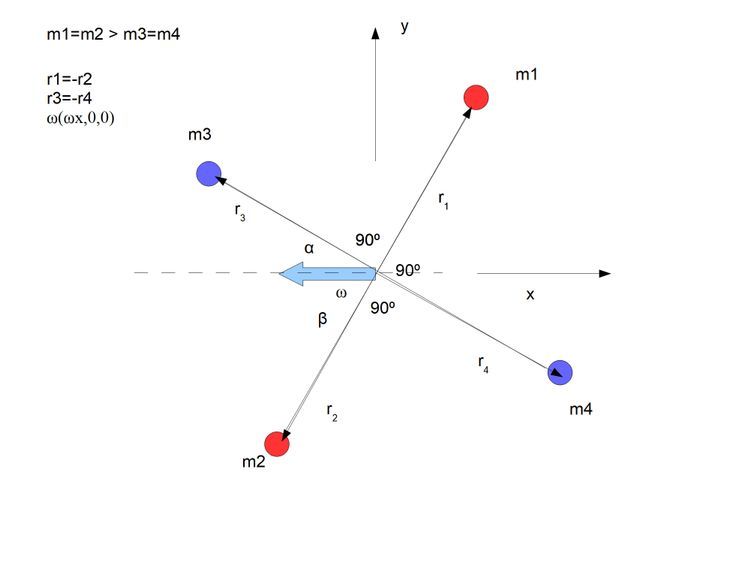
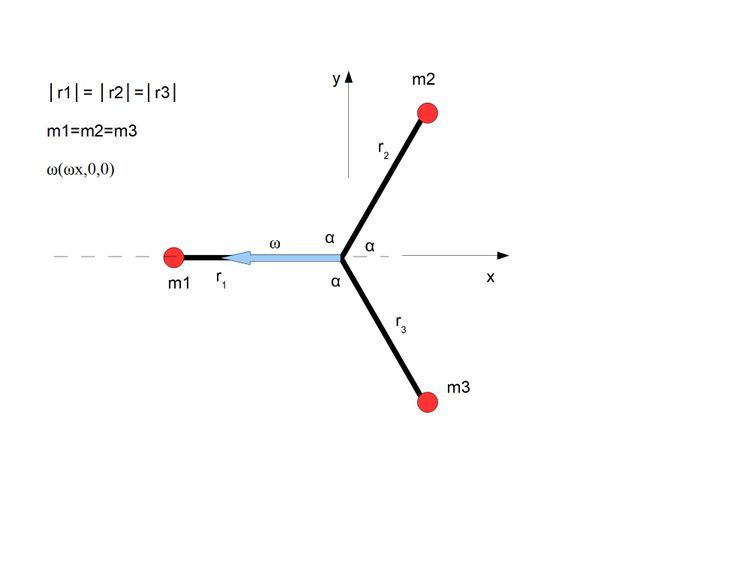
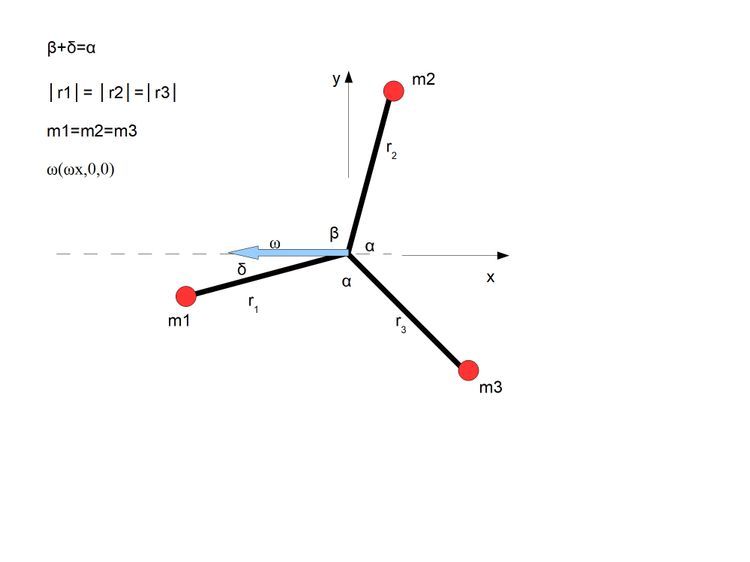
Wiem że wielu jest przeciwna mojej kalkulacji pozwalającej odwrócić równanie iloczynu wektorowego i w dodatku z użyciem odwrotności wektora, ale kalkulacja ta jest bardzo przydatna i co najważniejsze jest skuteczna. Przy jej użyciu można wiele uprościć i pokazać wiele detali bardzo przejrzyście i jeżeli komuś się ona nie podoba, to niejako nie mój problem :)
Nie mam możliwości wstawiania symbolu wektora dlatego będą one oznaczone po przez _, na przykład wektor A_. Przypomnę szybko jak odwrócić iloczyn wektorowy (działa jedynie kiedy kąt między wektorami jest równy 90°, w innych przypadkach wynik będzie nie poprawny). Ponieważ
A_ x B_ = C_
C_ jest pseudo wektorem. Wzory na wektory A_ i B_ to
C_ x 1/A_ = B_ (1)
1/B_ x C_ = A_
Aby stworzyć wektor 1/A_ będący odwrotnością wektora A_ (ax, ay, az) musimy jego współrzędne podzielić przez kwadrat jego modułu (długości)
 (2)
(2)
Cały dowód poprawności tego rachunku przedstawiłem tutaj
Zauważmy że kiedy moduł z wektora równy jest jeden |A|=1 to jego odwrotność równa się temu wektorowi
1/A_=A_ (3)
A więc kiedy przyjmiemy takie wartości by wektor ten równy był 1 to w zapisie znika ułamek wektora (2).
Kolejną ważną własnością iloczynu wektorowego którą będę używał jest następująca własność
A_ x B_ = |A||B|sinα =C_
Jeżeli wektory A_ i B_ nie są do siebie prostopadłe to w kalkulacji (w jednym z wektorów) bierze udział tylko składowa prostopadła do drugiego wektora, zaś składowa równoległa nie ma wpływu na wynik końcowy. To który z dwóch wektorów weźmiemy za punkt odniesienia nie ma wpływu na wynik końcowy.
Przykład
A_ (ax,0,0)
B_ (bx, by, bz)
B`_ (0, by, bz)
A_ x B_ = (0, -ax*bz, ax*by) = A_ x B`_ (4)
Możemy również za wektor odniesienia przyjąć wektor B_ i rozłożyć wektor A_ na składowe do niego prostopadłą i równoległą i zasada jest ta sama, a zmiana wektora odniesienia nie wpływa na wynik.
Teraz pare ważnych własności punktu w bryle sztywnej.
Jeżeli przyjmiemy układ współrzędnych gdzie środek masy znajduje się nieruchomo w środku układu współrzędnych, to punkt tej bryły który nie jest w środku ma tylko dwa wymiary swobody poruszania się i są one prostopadłe do wektora położenia tego punktu. Punkt nie może się przemieszczać równolegle do wektora położenia względem środka masy. Dla przykładu punkt m o współrzędnych (rx, 0, 0) może się jedynie poruszać z wektorem prędkości w kierunkach v_(0, vy, vz). (5)
Podczas swobodnego obrotu ciała sztywnego z nieruchomym środkiem masy, wektory prędkości liniowej jego punktów muszą spełniać równanie
v_ = Ω_ x r_ (6)
Bardzo ważną własnością BS jest fakt że wektor prędkości kątowej nie musi być prostopadły do wektora położenia punku r_ względem środka masy. Ma to swoje poważne konsekwencje i zrozumienie jak te wektory na siebie oddziałują, jest istotą zrozumienia mechanizmu obrotu ciał sztywnych.
Tu musimy troche pofilozofować i zrozumieć co jest rzeczywiste a co jest abstrakcją i pewne poziomy tej abstrakcji. W klasycznej Fizyce realna jest przestrzeń i czas oraz położenie punktów w tej czasoprzestrzeni. Każdy punkt ma swoje współrzędne [t](x,y,z) gdzie czas t jest niepowtarzalnym indeksem. Czas jest niepowtarzalny i płynie on w swoim równym tępię zawsze do przodu (mówimy o pojmowaniu klasycznym), współrzędne przestrzenne mogą się powtarzać i mogą też ulegać zmianie z różną prędkością. Zmiany współrzędnych przestrzennych w jakimś odcinku czasu nazywamy prędkością i przypisujemy jej wektor v_. Zarówno współrzędne jak i odcinek czasu czy wektor v_ nie są bytami realnymi (nie da się ich zobaczyć pod mikroskopem czy w jakiś inny sposób)a są jedynie analogiczną abstrakcją, sposobem zapisu i zrozumienia tego zjawiska przez nasze mózgi. Ta abstrakcja nie wystarczy aby opisać i zrozumieć ruch obrotowy, dlatego stworzono wyższy poziom abstrakcji oparty na iloczynie wektorowym i pseudo wektorach. Dlaczego o tym pisze? bo ważne jest aby zrozumieć że to wektory prędkości liniowej wraz z wektorami przyspieszeń dośrodkowych tworzą prędkość kątową a nie na odwrót, że prędkość liniowa jest wynikiem działania prędkości kątowej. Owszem możemy wyliczyć wektory prędkości za pomocą prędkości kątowej, ale nie zmienia to faktu że to prędkość liniowa jest bardziej rzeczywista.
Jakiś czas temu podałem wzór jak prędkości liniowe dla trzech prostopadłych do siebie punktów tworzą wektor chwilowej prędkości kątowej Ω_
 (7)
(7)
Wektory r1_ v1_ są to wektory położenia dla punktu m1 (rx, 0, 0)
Wektory r2_ v2_ są to wektory położenia dla punktu m2 (0, ry, 0)
Wektory r3_ v3_ są to wektory położenia dla punktu m3 (0, 0, rz)
Aby nie drażnić co niektórych wrażliwych można to policzyć dla punktów rx=1, ry=1, rz=1, wtedy znikają ułamki wektorów.
Dlaczego tak?
Dla przypadku gdy wektory r_ będą równe 1 używamy własności iloczynu wektorowego z punktu (4)
r1_ x v1_ = Ω_ (0, ωy, ωz) (8)
r2_ x v2_ = Ω_ (ωx, 0, ωz)
r3_ x v3_ = Ω_ (ωx, ωy, 0)
jak widzimy po zsumowaniu współrzędne tych trzech wektorów się dublują, dlatego potrzeba jest podzielić te wartości przez dwa. Jak widać aby uzyskać chwilowy wektor prędkości kątowej wystarczy znać położenie i prędkości dwóch prostopadłych do siebie punktów i umieć wydobyć z nich trzy współrzędne wektora prędkości kątowej Ω_.
Interesujące jest też zastosowanie tej metody do sytuacji płaskich gdzie dwa prostopadłe punkty i wektor prędkości kątowej znajdują się na jednej płaszczyźnie.
Mamy dwa punkty m1( rx, 0, 0); m2 (0, ry, 0) i wektor prędkości kątowej Ω_ (ωx, ωy, 0). Jak widać nie ma wartości na osi z. Prędkości liniowe dla punktów
v1_ = Ω_ x r1_ = (0, 0, -ωyrx) = ωy_ x rx_
v2_ = Ω_ x r2_ = (0, 0, ωxry) = ωx_ x ry_
Prędkość kątowa dla punktów, aby było łatwiej przyjmijmy że wartości rx=ry=1.
Ω1`_ = r1_ x v1 = (0, ωy, 0)
Ω2`_ = r2_ x v2 = (ωx, 0, 0)
Jak widzimy wektory prędkości kątowej dla dwóch prostopadłych do siebie punktów po zsumowaniu tworzą wektor prędkości chwilowej
Ω1`_ + Ω2`_ =Ω_ (9)

Powiecie że już znamy metody wyznaczania chwilowej prędkości kątowej, ale wszystkie które znam są metodami geometrycznymi, które w dodatku mają przypadki w których są nieskuteczne. Wymaga to sporej gimnastyki umysłowej jak te zależności geometryczne zaprogramować i ustalić warunki w których te metody są nieskuteczne i jak w takich przypadkach postępować. Moja algebraiczna metoda pozwala wyliczyć ten wektor w kilku prostych operacjach matematycznych i w dodatku zawsze jest skuteczna.
Jednak najważniejsze to poznanie czym jest prędkość kątowa i jak prędkości liniowe ją tworzą. Mając tą wiedze łatwo wyznaczamy wektory sił dośrodkowych działających na punkt. Zaczynając odpowiedź na schemat pierwszy. Mając wektor prędkości kątowej Ω_ oraz wektory położenia dla punktów liczymy wektory prędkości kątowej dla każdego punktu z osobna, używając następującego wzoru
v_ = Ω_ x r_ (10)
teraz można wyliczyć przyspieszenia dośrodkowe działające na punkty
ad_ = Ω_ x (Ω_ x r_) = Ω_ x v_ (11)
Wektor siły dośrodkowej to masa punktu razy jego przyspieszenie
F_ = ma_ (12)
Wszystko wygląda prosto ale to nie wszystko. Licząc w ten sposób okazuje się siła więzów nie jest prostopadła do wektora prędkości kątowej Ω_ (co już jest w sprzeczności z wiedzą książkową) i wstawiając jedynie taką siłę do algorytmów nie pozwala ona prawidłowo odtworzyć ruchu obrotowego ciała sztywnego. Ta metoda generuje tez sprzeczności w rachunkach.
Bierzemy schemat pierwszy i nadajemy wartości
Ω_ (-2, 0, 0); α=30°; β=60°; r3_(-√3/2, 1/2, 0)
v3_ = Ω_ x r3_ = (0, 0, -1)
przyspieszenie punktu m3 na kierunku osi y
a3y_ = Ω_ x v3_ = (0, -2, 0) (13)
ponieważ wartość |r3|=1 możemy teraz wyliczyć omegę prim ze wzoru
Ω3`˧_ = r3_ x v3_ = (-1/2, -√3/2, 0)
Ω3`˧_ jest prędkością kątową prostopadłą do wektora położenia punktu r3_
Liczymy teraz punkt m2 utrzymujemy wartość wektora położenia jako jeden |r2|=1 i znając kąt β ustalamy współrzędne wektora r2_ (-1/2, -√3/2, 0)
v2_ = Ω_ x r2_ = (0, 0, √3)
a2y_ = Ω_ x v2_ = (0, 2√3, 0)
Ω2`˧_ = r2_ x v2_ = (-3/2, √3/2, 0)
Nie ma niespodzianek zgodnie z dowodem (9) w płaskim przykładzie, suma prędkości kątowej dla dwóch prostopadłych punktów jest równa chwilowej prędkości kątowej
Ω3`_ + Ω2`_ = Ω_ (-2, 0, 0)
Do tej pory szło gładko ale zaczyna się sprzeczność. Oto schemat według tej interpretacji.
Schemat przedstawia wektory sił ale nasze wyliczone wektory przyspieszeń to a=F/m. Widzimy tu że nasze a3y_ jest jedynie składową y przyspieszenia a3_. Łatwiej to zobaczyć na tym schemacie (jest błąd wektor v powinien mieć przeciwny zwrot, osie x, y też są odwrotnie do naszego schematu)

A więc według tej interpretacji do naszych wyliczeń
|a3y| = |a3|sinα
|a3|=|a3y|/sinα=4
Więc składowa x tego przyspieszenia to
|a3x|=|a3|cosα=2√3
wektor przyspieszenia punktu m3 to
a3_ (-2√3, -2, 0)
sprawdzamy według Ω3`_ która jest prędkością kątową prostopadłą do wektora położenia m3.
a3`_ = Ω3`_ x v3_ = (-√3/2, -1/2, 0) (14)
Jak widać
a3_ ≠ a3`_
Bardzo długo trzymałem się tej książkowej interpretacji, zauważcie że ta książkowa interpretacja generuje niezerowe pary sił Fd3y_≠Fd1y_ równoległe do wektora prędkości kątowej Ω_ dający moment siły który w niektórych kalkulacjach dawał mi oczekiwany wynik, ale przy innych założeniach generował sprzeczności z którymi nie mogłem sobie poradzić.
Zauważmy że jeżeli użyjemy tej interpretacji prowadzi ona do złamania prawa zachowania momentu pędu. Zauważmy że przy tej interpretacji wektor prędkości kątowej Ω_ jest stały w czasie (co już jest sprzeczne z wynikami eksperymentalnymi gdyż w rzeczywistości wektor ten zmienia swą pozycje) oznacza to że wszystko kręci się wokół niego. Ponieważ wektor momentu pędu L_ nie musi być równoległy do Ω_, to w takim przypadku również wektor momentu pędu obracał by się wokół wektora prędkości kątowej, łamiąc w ten sposób fundamentalne prawo Fizyki. (15)

Czy to oznacza że książkowa interpretacja jest błędna? Nie do końca, okazało się że jest to jedynie fragment prawdy który trzeba było uzupełnić. Wszystko się zmienia kiedy przyjmiemy inną książkową interpretacje że siła więzów działająca na punkt jest zawsze prostopadła do wektora prędkości kątowej Ω_, czyli nie działa ona do środka masy a jest ona doosiowa zawsze prostopadła do osi obrotu.
Teraz nasze a3y_ (13) staje się wypadkową sił działającą na punkt czyli a3``_ a nie jak przedtem jedynie fragmentem innej siły.
a3``_ (0, -2, 0)
|a3``| = 2
Możemy teraz rozłożyć ten wektor na składową centralną do środka ciężkości a3c_ i składowa do niej prostopadłą a3p_.
a3c_ =a3``_ sinα = 1
a3p_ =a3``_ cosα = √3
Nasze a3c_ liczymy prędkości kątowej Ω3`_ dla punktu m3 co już zrobiliśmy w punkcie (14) jako a3`_
a3c_ (-√3/2, -1/2, 0)
|a3c_| = 1
Teraz trzeba policzyć drugą składową
a3p_ = a3``_ - a3c_ = ( √3/2, -3/2, 0)
|a3p_| = √3
Sprawdzamy jeszcze kąty z użyciem iloczynu skalarnego
cosα=(A_°B_) / (|A| |B|)
Ładnie nam wychodzi dla a3``_ i a3c_
cosα=1/2
a dla a3``_ i a3p_
cosα=√3/2
Czyli rachunek dla schematu pierwszego się zgadza nie ma już sprzeczności, przynajmniej ja nie znalazłem chociaż sprawdzałem na kilka sposobów. Jak sobie wyjaśniliśmy a3c_ jest wynikiem prędkości kątowej jaki posiada punkt ale skąd się wzięła a3p_? Jest to wynik działania prędkości kątowej równoległej do wektora położenia punktu.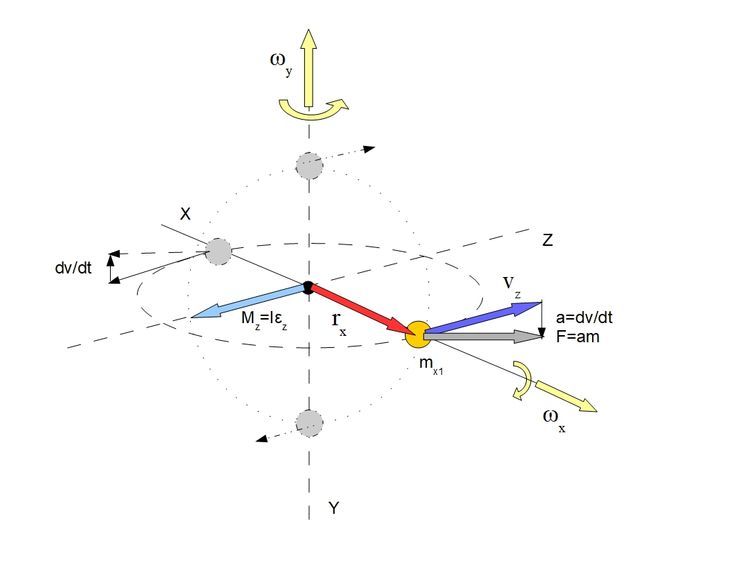
Jak widać na schemacie prędkość kątowa równoległa do ramienia obraca również wektor prędkości liniowej skutkując zaistnienia przyspieszenia w tym kierunku a_=dv_/dt i w konsekwencji powstania siły F_=ma_. Jak widać nic nie dzieje się bez przyczyny i wszystkie detale się zazębiają i uzupełniają.
Nasze przyspieszenie a3``_ daje wypadkową siłę więzów F3_ =ma3``_. Nazywam ją siłą więzów bo to właśnie odziaływanie więzów tą siłę tworzą. Muszę tu rozdzielić siłę więzów od siły centralnej. Siła centralna Fc_ jest siłą zawsze skierowaną do środka ciężkości i wynika ona i wynika ona z posiadanej przez punkt prędkości kątowej Ω3`_ jednak istnieje jeszcze siła spowodowana prędkością kontową drugiego prostopadłego ramienia Ω2`_ która jest równoległa do wektora położenia a skutkuje powstaniem siły którą ja nazwałbym kręcącą Fk_. Siła kręcąca z siłą centralną po s=zsumowaniu daje nam wypadkową siłę więzów działającą na punkt
Fw_=Fc_+Fk_
Istnienie siły kręcącej jest w pełni zgodne z równaniami Eulera dla ruchu obrotowego co udowadniałem w innej notce.
https://www.salon24.pl/u/przestrz/878010,schemat-mechaniki-obrotu-bryly-sztywnej
Równanie Eulera można łatwo uprościć
I(dΩ/dt) + Ω x IΩ = 0
dΩ/dt - to przyspieszenie kątowe
I(dΩ/dt) - to moment siły M
IΩ- to wektor momentu pędu L
Cała magia matematyki opisująca rzeczywistość polega na tym że te wszystkie skomplikowane wyliczenia, te zawiłe mechanizmy upraszczają się ostatecznie do prostego wzoru
M = L x Ω
Brak tego momentu siły musiał by skutkować złamaniem prawa zachowania momentu pędu i zadziwiające że powstaje właśnie taki aby te prawo utrzymać. Ten moment siły jest zawsze prostopadły do wektor momentu pędu, a całe przyspieszenie kątowe odbywa się na składowej prędkości kątowej prostopadłej do wektora momentu pędu.
Gdy nieznajome niby bardzo skomplikowane ale jakież proste po poznaniu.










Komentarze