Obecnie uważa się że aby opisać mechanikę obrotu konkretnej bryły sztywnej (BS), to przede wszystkim należy poznać jej trzy główne momenty bezwładności (każdą BS można tak zapisać), a rozmieszczenie poszczególnych punktów (mas) służy jedynie do wyliczenia tych momentów bezwładności i informacje te są już później nieistotne. czyli dwie BS o różnych pozycjach mas ale z tymi samymi momentami bezwładności, będą się zachowywać identycznie podczas takiego samego ruchu obrotowego.
O tym że za ruch obrotowy odpowiadają siły więzów wiadomo już od dawna, ale odpowiedź jak te siły działają na konkretny punkt BS uznano za wiedze do niczego nie przydatną i zbędną i całkowicie ją zaniedbano. Wiemy jak się zachowuje BS, to po co nam wiedzieć co się dzieje z jej punktem, jak on pracuje? Większość normalnych nie widzi sensu w szukaniu odpowiedzi, ale mnie to akurat zainteresowało i chcę to wiedzieć dla samego faktu poznania. Jak to jest że różne BS zachowują się tak samo? Dlaczego ważny jest moment bezwładności a nieistotne jest położenie punktów? Jak te punkty wzajemnie na siebie oddziałują?
Takie książkowe modle gdzie rozkład mas w BS ma trzy osie symetrii zostały już rozpracowane do najmniejszego szczegółu w dwóch moich poprzednich notkach
https://www.salon24.pl/u/przestrz/896396,kalkulacje-sil-wiezow-podczas-obrotu-cial-sztywnych
https://www.salon24.pl/u/przestrz/899050,kalkulacje-sil-wiezow-podczas-obrotu-cial-sztywnych-cz2
Ale są to modele wyidealizowane i wirtualne, a BS mogą mieć różne kształty również niesymetryczne, jak wtedy działają te punkty, jakie działają na nie siły? Na daremno szukać odpowiedzi na te pytania w książkach, bo jest to wiedza niepotrzebna i przeklęta, nie porozmawiasz też o tym z Fizykiem bo ten od razu zwyzywa cię od nieuków, że takie głupie pytania zadajesz. Więc nie pozostaje nic jak odpowiedzi na to pytanie znaleźć samemu.
Ponieważ odkryłem że mimo obecnego zaawansowania w nauce są ogromne luki, jak na przykład przegapienie wewnętrznego momentu siły odpowiadającego za mechanikę bryły sztywnej czy efekt Dzanibekowa
Który już dawno wyliczyłem i udowodniłem na mnóstwo różnych sposobów, który obecny mędrcy uznali za bluźnierstwo i herezje (dla nich ziemia dalej jest płaska), przez jakiś czas miałem nadzieje że może przegapili oni coś jeszcze. Zastanawiałem się czy czasem asymetryczne rozmieszczenie mas nie skutkuje jeszcze jakimś efektem który nauka po prostu przegapiła.
Moje pierwsze szacunki i kalkulacje dawały taką nadzieje ale moje własne amatorskie eksperymenty w warunkach domowych okazały się negatywne i nie udało mi się nic ciekawego uzyskać. W jednym eksperymencie były minimalne wyniki ale ich weryfikacja po przez odwrócenie ramion okazała się negatywna a powrót do pierwotnych ustawień nie dawał powtarzalnych wyników.
Dlaczego więc asymetryczne BS zachowują się tak samo jak symetryczne BS? I jak działają siły więzów które powinny być centralne, ale gdyby tak było w asymetrycznych BS powinny się one nie zerować?
Luźne ramie na którym jest zamontowana masa się unosi ale usztywnienie tego ramienia nie daje już tego efektu, czyli siły na niego działającą są inne. Skąd punkt wie że jest na ramieniu sztywnym czy luźnym?
Muszę tu zaznaczyć ze podaje odpowiedź którą uważam za najbardziej prawdopodobną, być może nawet się ona bardzo spodoba Fizykom ale nie mogę być tego pewny w 100% do czasu weryfikacji eksperymentalnej. Musze tu zawierzyć matematyce, tym że prawidłowo umiem to policzyć i tym że prawo Fizyki również tutaj działa mimo że nikt nigdy tego nie sprawdził.
Ponieważ zakładamy poprawność założenia że liczy się jedynie moment bezwładności a rozłożenie mas nie ma tu istotnego wpływu, to zacznijmy od wyliczenia momentów bezwładności mojej niesymetrycznej BS i transformacji w ciało symetryczne. Pomoże nam to zrozumieć dlaczego położenie punktów jest nie istotne.
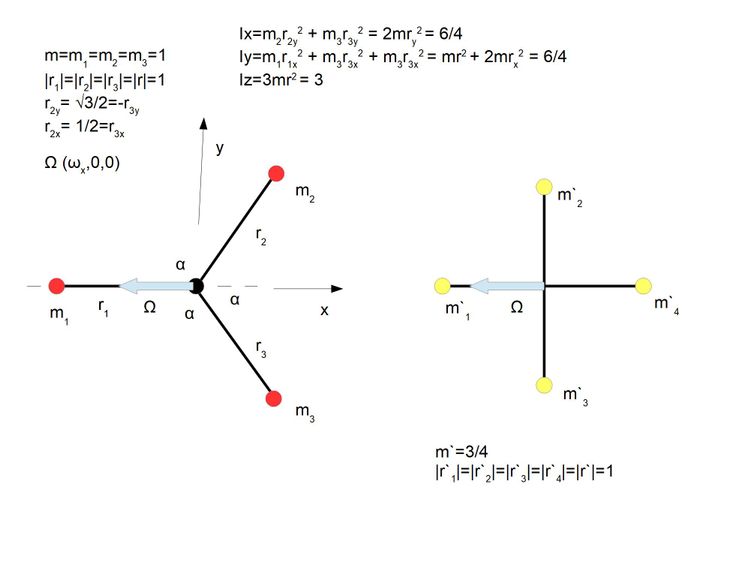
Po lewej mamy BS której dotyczy pytanie. Po prawej BS` z takimi samymi momentami bezwładności jednak rozkład mas symetryczny względem wszystkich osi głównych.
Obliczymy najpierw BS` który jest książkowym przykładem aby mieć punkt odniesienia. Normalizujemy wartości a właściwie zostaje jedynie wartość prędkości kątowej ωx=-1.
Oczywiście m`1 i m`4 leżą na osi obrotu ich wektory prędkości równe są zero, czyli też działające na nich siły więzów równe są zero. Liczymy więc wektory prędkości dla m`2 i m`3 ze wzoru
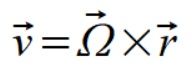(1)
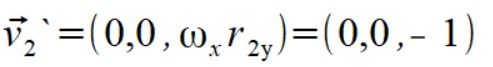
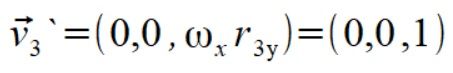
następnie liczymy przyspieszenia dośrodkowe ze wzoru
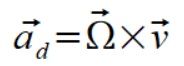(2)
i siłę więzów
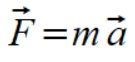
mamy więc parę symetrycznych sił które się zerują
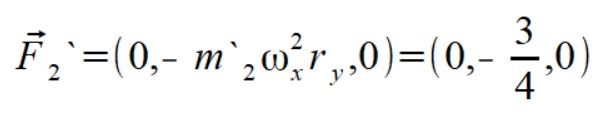
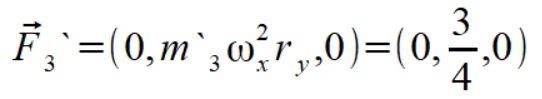
Przejdźmy więc do wyliczenia sił dla punktów pierwotnej BS moją metodą. m1 znajduje się na osi obrotu więc prędkość i siła na niego działająca jest zero. Wyznaczamy więc prędkości dla punktów m2 i m3 ze wzoru (1)
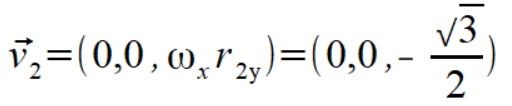
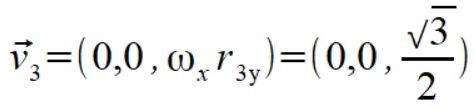
Rozkładamy teraz wektor prędkości kątowej na składowe prostopadłą i równoległą do wektorów położenia. Używamy wzoru
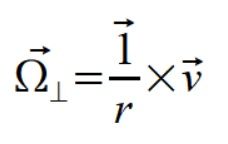(3)
|r|=1 czyli 1/r=r
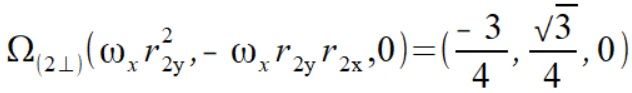
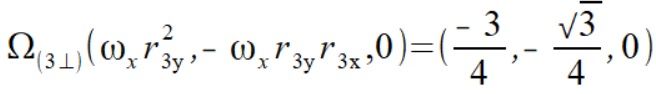
Liczymy wektory prędkości kątowej równoległy do wektorów położenia
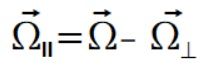(4)
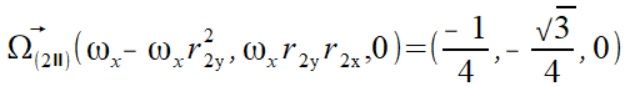
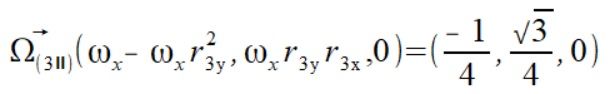
Muszę tutaj zauważyć pewną różnice z tym jak wyglądają te prędkości kątowe kiedy mamy ramiona do siebie prostopadłe a kiedy one prostopadłe do siebie nie są. Zauważmy że w BS` prędkość kątowa równoległa do jednego ramienia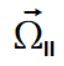 
jest równocześnie prędkością kątową prostopadłego do niego ramienia i na odwrót.
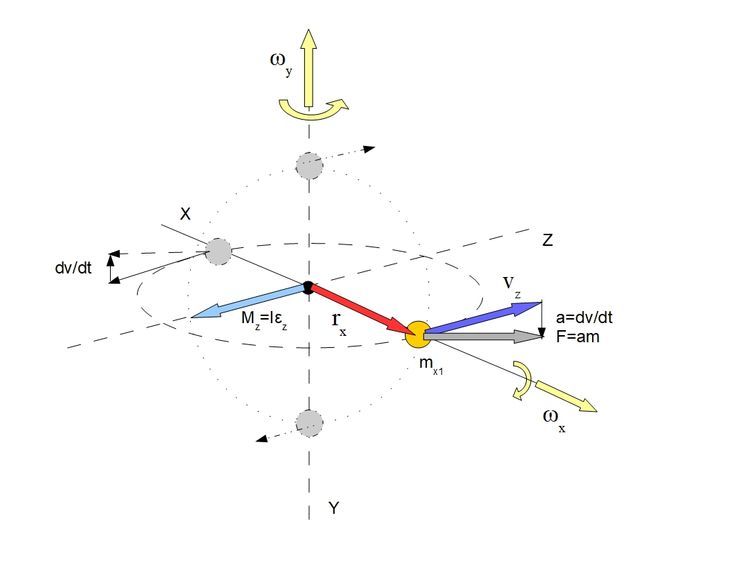
Więc w tym modelowym przykładzie przyczyną powstania siły na jednym ramieniu jest prędkość kątowa drugiego ramienia. W naszym przykładzie BS, prędkości kątowe równoległe do ramienia nie są jednocześnie prędkościami kątowymi innego ramienia.
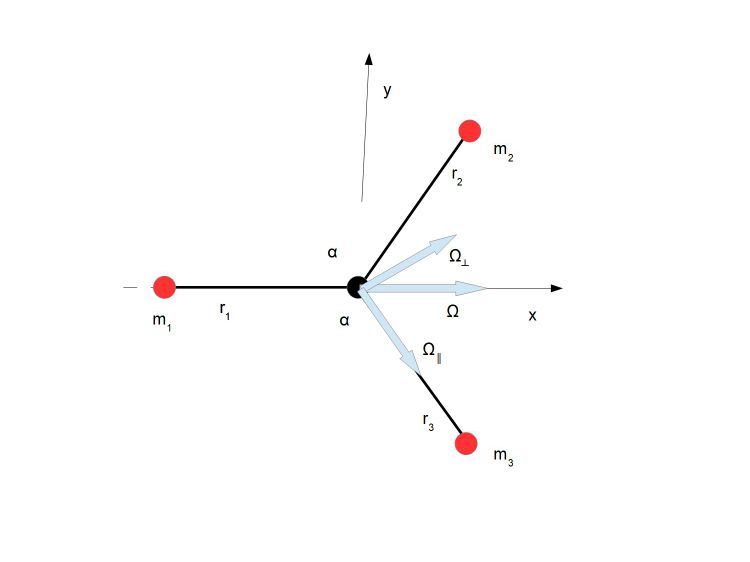
Musze teraz zaufać Interpretacji Fizyki że siły dośrodkowe zawsze są skierowane do środka masy, dlatego liczę prędkość kątową prostopadłą do wektora położenia, bo ta prędkość wskazuje tą siłę
Musze też zaufać matematyce że poniższy wzór na przyspieszenie dośrodkowe jest zawsze prawdziwy
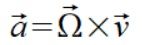(5)
Liczymy więc te przyspieszenia dla naszych punktów używając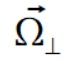 
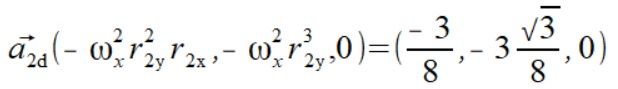
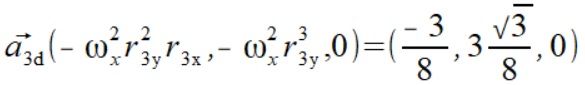
Liczymy też przyspieszenia z tego samego wzoru (5) używając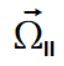
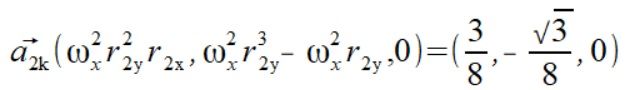
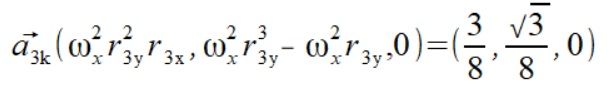
Sumując teraz przyspieszenia a_ = ad_ + ak dla punktów uzyskujemy dwie przeciwne siły które po dodaniu się zerują.
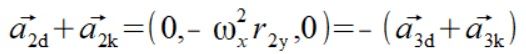
Prawdę mówiąc sam jestem trochę zaskoczony bo przypuszczałem że siły się niezerującą i trzeba będzie użyć trzeciego prawa dynamiki by wyznaczyć siłę reakcji, ale wygląda na to że ten skomplikowany mechanizm jest tak dostrojony że siły więzów zawsze się zerują. Aż trudno uwierzyć że tyle zmiennych tak są skoordynowane by się zerować, wystarczy jedynie wiedzieć jak liczyć.
Jak teraz nasze BS się ma do BS`?
Kierunki działania wypadkowej siły na punkty są prostopadłe do wektora prędkości kątowej i wektor momentu pędu jest dla obu brył taki sam. A dla równania Eulera ruchu obrotowego ciał sztywnych istotne są jedynie tensor momentu bezwładności i prędkośc kątowa.
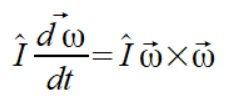
Nowe wyliczenia dają nowe odpowiedzi ale też generują następne pytania. Teraz moja BS nie za bardzo mi się podoba, być może poprawny wynik jest jedynie szczęśliwym trafem i gdy zmienię ustawienia punktów to nie wszystko się tak pięknie zgra. jak udowodnić że te siły będą się zerować zawsze? Duży krok do przodu ale meta znów się oddaliła:)
