Kłopotliwe twierdzenie Noether

Zacznę od (prawdziwej) anegdoty z IV piętra. Na jednym z wykładów z mechaniki klasycznej wykładowca tak mniej więcej zaczął swój przekaz: Zdaję sobie sprawę,  że to, co wykładam może być trudne, ale zawsze mogłem liczyć przynajmniej na jednego słuchacza, który zrozumie wykładany materiał. Myślę o sobie. Niestety, dziś nie mogę liczyć nawet na tego jednego. O czym miał mówić ów fizyk? O twierdzeniu Emmy Noether.

Jest to bardzo ważne twierdzenie w fizyce, bo łączy dwie rzeczy: symetrie i prawa zachowania. No i jeśli nie jesteś fizykiem czy matematykiem, to możesz nie chcieć czytać dalej, ale zachęcam, by tak nie robić i mimo wszystko zajrzeć do dalszej części tekstu.[1]

Zanim zaczniemy, jedna uwaga dla osób, które twierdzeniem już znają: Rozpatruję przykład, gdzie siły nie zależą od czasu oraz nie biorę pod uwagę symetrii związanych z czasem. Wbrew pozorom uwzględnienie jawnej zależności od czasu, wymaga poszerzenia modelu i nie jest tylko dopisaniem jednej literki t.

Twierdzenie

Do jednego z najważniejszych twierdzeń w fizyce – wyrażonego we współczesnej postaci –  potrzebne są trzy rzeczy:

• specjalna funkcja, której dziedziną są  położenia i prędkości, nazywana lagranżianem;
• symetrie (przekształcenia dziedziny lagranżianu) zachowujące wartości lagranżianu;
• wzór z którego wyliczymy stałe ruchu (prawa zachowania), czyli „treść” twierdzenia.

Można przygotować sobie te rzeczy tak, żeby samo twierdzenie było łatwe do ogarnięcia, można tak zaciemnić sprawę, że pozostanie nam dzielenie losu z wykładowcą z początkowej anegdotki. Spróbujmy przejrzeć te punkty.

Lagranżian L jest funkcją, której dziedziną jest zbiór możliwych położeń i prędkości. Zwykle pisze się lagranżiany, wręcz ukrywając fakt, jaka jest ich dziedzina, bo w przeciwnym razie może to rodzić niepotrzebną ciekawość i wątpliwości u młodych fizyków. Niektóre podręczniki niesłusznie i mętnie sugerują, że w operacjach z udziałem funkcji L wystarczy posługiwać się zbiorem samych położeń, czyli tzw. przestrzenią konfiguracyjną – nazwę ten zbiór M. Ale jak ktoś już chce jednak wiedzieć, to dowie się, że dziedzina L nazywa się przestrzenią styczną i oznacza się go TM. Zarówno nazwa jak i oznaczenie nie są jednak istotne dla niniejszej notki. Dla nas będzie ważne, że TM to zbiór możliwych położeń q i prędkości v:

L: TM ∋ (q, v) ↦ L(q,v) ∈ R

Zapis q oznacza symbolicznie wszystkie współrzędne położenia qⁱ. Podobnie dla prędkości – będziemy mieli tyle współrzędnych vⁱ, ile jest stopni swobody. Współrzędne te pojawią się we wzorze końcowym twierdzenia.

Istnieją mniej lub bardziej szczegółowe przepisy, jaka ma być L, żeby odpowiadała danemu przypadkowi fizycznemu.

Funkcja L służy do rozwiązywania tzw. równań Lagrange'a, czyli dowiedzenia się, jak będą wyglądały położenie i prędkość ciała w przyszłości (i jak wyglądały w przeszłości), jeśli znamy jego początkowe położenie i prędkość. W samym twierdzeniu Noether, równania te jawnie nie występują, choć są rzecz jasna wykorzystywane w dowodzie.

Pora na symetrie. Nie będę szczegółowo objaśniał czym są, bo połowa poprzedniej notki jest temu poświęcona. Przypomnę, że na podstawie jednoparametrowej grupy przekształceń ψ_s na M, znajdujemy jednoparametrową grupę ϕ_s na docelowym zborze, czyli TM. I tu jest mały zgryz, bo na pierwszy rzut oka wcale nie widać, jak na podstawie transformacji

ψ_s: M ∋ q ↦ ψ_s(q) ∈ M

odnaleźć odpowiadającą jej transformację φ_s również dla prędkości:

φ_s: TM ∋ ( q, v ) ↦ φ_s(q ,v)  ∈ TM

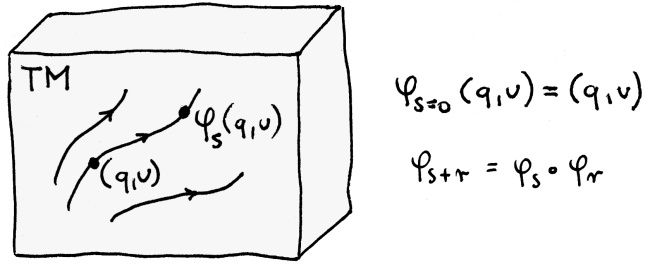
Znaczy się dla konkretnych przypadków, które są przykładami w podręcznikach (przesunięcia, obroty), przekształcenia na prędkościach są trywialne i nie budzą wątpliwości. Skoro jednak mamy ogólne twierdzenie, wypadałoby wiedzieć, jak to działa w przypadku ogólnym. Ciekawskich odsyłam do świetnego podręcznika „Metody matematyczne mechaniki klasycznej” W. Arnolda.

Wracajmy do wyliczanki. Wypisuję założenie twierdzenia: φ_s jest takim przekształceniem na TM, że langranżian jest niezmienniczy:

∀ (q, v) ∈ TM: L( q, v ) = L( φ_s(q, v) )

No i teza: Jak mamy to wszystko co powyżej, to dla każdej symetrii φ_s istnieje jedna całka ruchu I, czyli taka funkcja na TM, że rozwiązania równania  Lagrange'a nie wychodzą poza jej poziomice. Innymi słowy trajektorie (q_t, v_t) „poruszają” się po poziomicach I, czyli   I( q_t, v_t ) = const dla każdego t. No to jeszcze wypiszmy ten wzór na całkę:

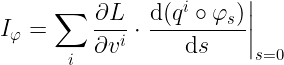
Ten drugi człon iloczynu trochę straszy wyglądem, ale jest dość oczywisty przy obliczeniach, co zobaczymy na przykładzie już za chwilę. Powyższy wzór nie jest ładny, bo jawnie zależy od konkretnego układu współrzędnych na przestrzeni TM. Ze znanych mi podręczników, jedynie W. Arnold pochyla się nad niezależnością całki ruchu od wyboru układu.

II prawo Keplera

Skoro tyle powypisywałem wzorów, uzasadniając, że to łatwe, pora na przykład. Przykładem tym będzie wyprowadzenie II prawa Keplera za pomocą twierdzenia Noether.

Na początek lagranżian, czyli funkcja, która jest pomocna przy rozwiązywaniu równań ruchu (których nie będę tu wypisywał ani tym bardziej rozwiązywał). Warunki fizyczne: nieruchome centrum (Słońce) przyciągające planety. Oddziaływanie ma energią potencjalną ~(-1/r). Ograniczę się od razu do ruchu na płaszczyźnie – analiza symetrii zadania powinna nas przekonać, że to słuszne posunięcie.

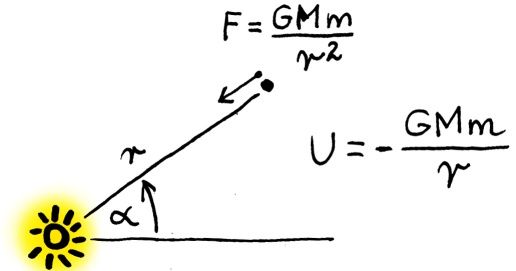
Jak widać, położenie opisane jest przez dwie współrzędne: r – odległość od centrum i α – kąt. Pamiętając I prawo Keplera  z lekcji fizyki, powinniśmy wiedzieć, że w trakcie ruchu  mogą zmieniać się obie te współrzędne planety.

Argumentami lagranżianu są nie tylko r i α, ale również  odpowiadające im prędkości. Wypadałoby trochę uzasadnić dlaczego są to v_r – prędkość oddalania/przybliżania się od/do Słońca i ω – prędkość kątowa, ale w tym celu, to należałoby napisać podręcznik, a w notce planuję jedynie zastosować jedno twierdzenie. Zauważmy jedynie, że ω wcale nie ma wymiaru prędkości.

W ten sposób dostaliśmy układ współrzędnych na  przestrzeni TM – przestrzeni położeń i prędkości – jest to czwórka funkcji: { r, α, v_r, ω }. Skoro tak, to wypiszę lagranżian, który w wielu przypadkach jest różnicą energii kinetycznej i potencjalnej. Tak też jest i tu:

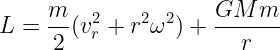
gdzie  GMm oznacza iloczyn stałej grawitacji, masy Słońca i masy planety.

Pora przystąpić do punktu drugiego i znaleźć jakieś transformacje niezmiennicze. Akurat powyższy przypadek jest dość charakterystyczny, bo jeśli lagranżian nie zależy od któreś współrzędnej, to ona właśnie będzie naszym kandydatem do przekształceń. Ponieważ L nie zależy od α, wykorzystamy ją do utworzenia transformacji. Zaproponuję  zwykłe obroty:

ψ_s( α ) = α + s

bez zmiany r. To dobre przekształcenie, bo jest grupą, a dla s=0 dostajemy identyczność, czyli grupową jedynkę. Jak φ_s będzie zmieniać prędkości? Otóż nie będzie ich zmieniać. Dla v_r jest to dość oczywiste, bo nasza transformacja nie dotyka r. Intuicyjny argument, że transformacja nie zmieni ω wygląda następująco (s nie ma nic wspólnego z czasem t):

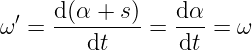
Bardziej ambitni zauważą, że powyższy wzór ma sens, dla konkretnych, jednowymiarowych trajektorii na M. Ale żeby opisać to porządnie, należałoby się zastanowić, jak definiowane są prędkości, co jak już wspomniałem wcześniej, wymagałoby napisania podręcznika. Więc pozostańmy na razie przy tym zgrubnym argumencie.

Podsumujmy jak wygląda przekształcenie na MT:

φ_s: MT ∋ (r, α, v_r, ω) ↦ (r, α+s, v_r, ω) ∈ MT

Mam wyrzuty sumienia, że tymi samymi literkami oznaczam funkcje współrzędnych jak i same współrzędne punktów TM czyli liczby. Ale jak napisałem kilka notek wcześniej, nie sposób walczyć z tradycją oszczędzania symboliczno-literkowego. Wracając do tematu: łatwo zauważyć, że powyższa transformacja nie zmienia lagranżianu. Czyli jest jego symetrią. Pora więc wyliczyć stałą ruchu odpowiadającą tej symetrii.

Wypiszmy jawnie wzór na całkę ruchu:

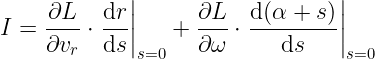
Pierwszy człon jest zerowy, gdyż r nie zależy od s, a pochodna w drugim członie jest równa 1 i nawet nie trzeba podstawiać s=0.

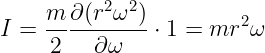
Osoby zaznajomione z fizyką od razu rozpoznają wyrażenie na moment pędu. Tym, co nie widzą od razu, może więcej wyjaśni rysunek:

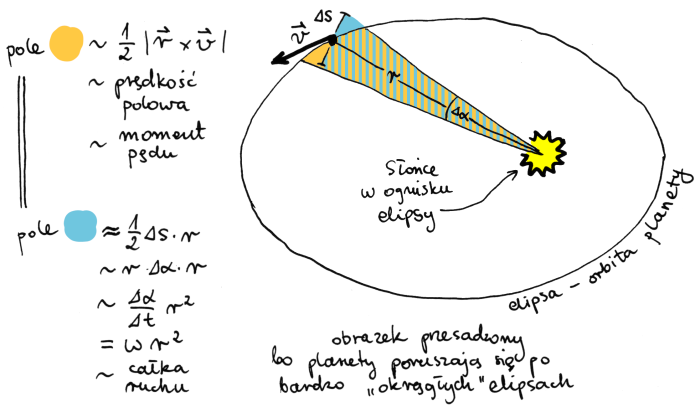
Pora na małe podsumowanie: Pomimo, że nie rozwiązaliśmy równań Lagrange'a – właściwie to nawet ich nie wypisałem – odnaleźliśmy wielkość, która jest zachowana podczas ruchu. Dla ruchu planet wokół Słońca, jest nią moment pędu. Przy okazji przetestowaliśmy jedno z najważniejszych twierdzeń w fizyce teoretycznej.

Gdybyśmy jednak rozwiązali równania ruchu, okazałoby się, że nie tylko elipsy, na które się powoływałem, są możliwymi torami. Dla parabol i hiperbol, wielkość mr²ω też jest zachowana, choć ciężko powiedzieć, że kometa, która raz w swym życiu odwiedza Układ Słoneczny, krąży wokół Słońca, a z takimi ruchami kojarzy nam się zwykle pojęcie momentu pędu.

Spostrzegawczy czytelnicy zauważą też, że jeśli chodzi o energię potencjalną, to wykorzystany był jedynie fakt, że nie zależała ona od α. Dlatego moment pędu będzie zachowany dla każdej siły nie zależącej do kątów,  a jedynie od odległości od centrum siły.

* * *

Może gdyby wykładowca z anegdotki  zajrzał do wspomnianego podręcznika Arnolda, nie czułby się tak osamotniony na swoim wykładzie.

[1] Przypomina mi się fragment opowieści o pewnym księdzu prowadzącym rekolekcje. Otóż wygłaszał on kazanie, które wcześniej pracowicie sobie przygotował, by było jak najlepsze. I rzeczywiście, już po wszystkim przyszedł do niego jakiś wierny i rzekł „Słuchałem kazania, jakie ksiądz wygłosił i muszę powiedzieć, że się nawróciłem”. Kaznodzieja ucieszył się niezmiernie i spytał, co  przekonało nawróconego. Ciekawiło go, które z użytych argumentów okazały się najbardziej skuteczne. ,,Jak słuchałem tego kazania, to widziałem, że ksiądz wkładał w nie tyle energii, że aż grdyka księdzu skakała. Pomyślałem – pewnie to o czymś bardzo ważnym, skoro ksiądz się tak angażuje. To mnie przekonało i dlatego postanowiłem poprawić swoje postępowanie”. Ale może ze zrozumieniem sensu notki, nie będzie aż tak źle? ☺