Tradycja przedstawiania matematyki w tekstach popularnonaukowych zawiera w sobie (między innymi) dwie przeciwstawne tendencje.
Pierwsza opiera się na zachwycie: jak magicznie odwzorowuje ona rozmaite elementy rzeczywistości. Czasami robi się to efekciarsko, czasami bardziej rzeczowo. Spotkałem się kiedyś z takim efekciarskim podejściem przy opisywaniu roli geometrii różniczkowej Riemanna. Że twórca ją sobie napisał w XIX wieku, a w XX czarodziejsko stała się ona podstawą OTW. Zdamy sobie sprawę, z tego że ta opowieść ma niewielką wartość merytoryczną, jeśli zauważymy, że formalizm tensorowy, który jest głównym narzędziem stosowanej w OTW geometrii Riemanna, jest jednak dość późnym wynalazkiem – elektrodynamika, dla której też się go stosuje, została sformułowana wcześniej. Ale zachwyt nad akuratnością matematyki może mieć też racjonalniejsze podstawy. Tak właśnie opisywałem np. efekt Starka.
Druga tendencja – zdecydowanie bardziej atrakcyjna – to pokazywanie jak matematyka jest dziwna i zaskakująca. Ta łatwa droga epatowania rozmaitymi egzotycznymi obiektami, też nie jest mi obca – w końcu taka była moja seria o liczbach. Przyznaję: to dość nęcący sposób opowiadania o królowej nauk. No bo czyż to nie piękne, że bierzemy zwykłą kulę, i szast-prast, hokus-pokus: z jednej robimy dwie takie same. Albo konstruujemy ciągłą linię, która wypełni sobą kwadrat. Albo bierzemy odcinek o długości 1, wyrzucamy z niego kolejne odcinki o łącznej długości 1 i zostaje wciąż tyle samo punktów, co było na początku. Toż to przecież, jak królik z kapelusza, a nawet lepiej bo nie trzeba oszukiwać!
Obie drogi, pomimo wad, są wartościowe, bo zachęcają ludzi do zaznajomienia się z matematyką. Jednak seria planowanych przeze mnie notek, ma zamiar iść jeszcze innym tropem. Bo z zastosowaniem matematyki jest trochę tak, jak z wykorzystaniem drewna. Kiedyś pewien budowlaniec przekonywał mnie, że to materiał idealny, ale nie ukrywał, że nieraz trzeba włożyć dużo wysiłku by go użyć.
Tematem kilku planowanych tekstów jest wykorzystanie przestrzeni Rn. W prawdziwych zastosowaniach, rzadko kiedy potrzebujemy wszystkich współrzędnych od –∞ do ∞, więc spokojnie można przyjąć, że będę pisał o przyzwoitych podzbiorach tych przestrzeni.
Co nam daje Rn?
Od jakiegoś czasu geometryczne punkty, którymi zajmowali się już starożytni Grecy, są dwójkami czy trójkami liczb rzeczywistych. Punkt na prostej to jedna liczba. Na płaszczyźnie będą to dwie liczby należące do iloczynu kartezjańskiego R×R. Przestrzeń to trzy liczby z R×R×R. Zapis Rn oznacza, że przestrzeń jest iloczynem kartezjańskim n prostych R, a jego elementami jest paczka n liczb (współrzędnych punktu).
Pomysł, żeby byty geometryczne traktować jako zbiory liczbowe, pochodzi zdaje się od Kartezjusza i jest bardzo wygodny, co więcej wprowadza dodatkowe bonusy. W końcu – jak to mówią – od przybytku głowa nie boli.
Zobaczmy jakie to podarunki daje nam Rn. Przede wszystkim każdemu punktowi możemy przyporządkować liczbę „odległość od środka układu współrzędnych”. Nazwa niekoniecznie mądra. Zresztą możecie sobie ją nazwać inaczej, najważniejsze, że w zgodzie z twierdzeniem Pitagorasa da się ją wyliczyć (kropki oznaczają, że współrzędnych może być więcej niż 3):
|A( x, y, z, … )| = √( x2+ y2+ z2 + … )
Interpretacja tej liczby jest trochę słaba, ale jak najbardziej możemy wykorzystać ją do znalezienia odległości między punktami:
d( A, B ) = | A–B |
Oj! Widać, że ponieważ punkty zrobione są z liczb, to można je od siebie odejmować. Na przykład po to, żeby obliczyć odległość między nimi, tak jak powyżej. Ale skoro tak, to można też je dodawać i mnożyć przez liczby. No tak, powiedzmy to na głos: Nasze przestrzenie i płaszczyzny są „przy okazji” przestrzeniami wektorowymi, a każdy ich punkt jest wektorem.
Wypisany powyżej wzór, to nic innego jak kwadrat punktu/wektora liczony przy pomocy iloczynu skalarnego:
(A, B) = xA xB + yA yB + zA zB + …
Przy okazji, skoro mamy iloczyn skalarny, to możemy od razu mierzyć kąty w naszych przestrzeniach. Na przykład wiemy jak sprawdzić, czy coś jest prostopadłe czy nie.
Bonusów ciąg dalszy: Bez większych ceregieli określimy objętość czy pole co ładniejszych figur. Każda przestrzeń Rn, posiada bowiem naturalny wzorzec/jednostkę n-wymiarowej objętości. Jest nim n-kostka o wymiarach 1×1× …1. Dla płaszczyzny to kwadrat, a dla przestrzeni sześcian:
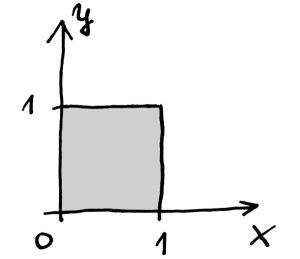
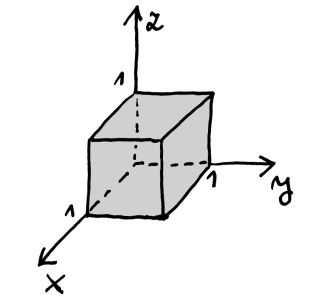
Może nawet nie zauważyliśmy, ale od dłuższego czasu posługujemy się tzw. kartezjańskim układem współrzędnych. Nie musimy go nawet specjalnie definiować: Każda współrzędna odpowiada kolejnym liczbom, z których budujemy punkty przestrzeni:
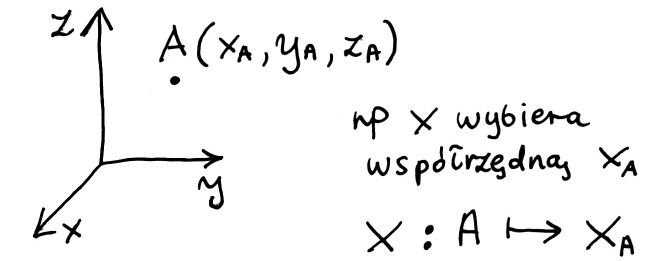
I na koniec listy (choć na pewno nie jest kompletna) dołóżmy jeszcze prosty sposób na liczenie pochodnych cząstkowych funkcji. Tu mały cytat obrazkowy z „Analizy” Maurina:
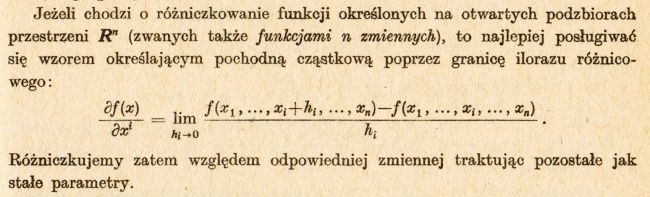
Funkcja ma tyle zmiennych, co wymiar Rn. Jak umiemy policzyć pochodną w jednym wymiarze, to policzymy pochodną dla każdej zmiennej. Bo każda zmienna odpowiada jednej współrzędnej z Rn.
* * *
Zamknijmy na razie listę prezentów od Rn. Od krytycznej oceny ostatniego z nich zacznę następny odcinek serii. Bo pomimo, że wyżej wypisane bonusy wydają się wartościowe, czasami od przybytku głowa jednak boli.

