MM&AlK.
Zanim zaprojektujemy bryłę złotej piramidy, jej komór i poziomów ich lokalizacji, niezbędnym jest powiedzenie paru zdań o wzorcu długości i liczbach…
Łokieć królewski
Na temat egipskiego wzorca długości (łokcia królewskiego), trwają co rusz dyskusje prowadzone przez zwolenników aktualnych poglądów na powstanie piramid oraz zwolenników tzw. piramidologii, czyli przeciwników poglądów akademickich...
Odnosząc się do pomiarów piramid autorzy wspierający poglądy akademickie piszą: ... W tym miejscu należy zwrócić wagę na istotny fakt: rozważając jakiekolwiek wymiary budowli egipskich, trzeba pamiętać, że w starożytnym Egipcie były one wyznaczane za pomocą naturalnych jednostek miar, jakie człowiek „odkrył” wręcz w zaraniu dziejów, ponieważ stale mu towarzyszyły - palców, dłoni i łokcia (tzn. długości ramienia od czubków palców do łokcia). W czasach budowy piramid te jednostki miar były już od dawna ujednolicone i stosowane w przyrządach mierniczych. Podstawową miarą był łokieć królewski o długości nieco ponad 52 cm (52,36 cm), który dzielił się na 7 dłoni (po 7,48 cm), dłoń zaś na 4 palce (o długości 1,87 cm). Jak widać, te jednostki egipskie niezbyt „przystają” do naszego systemu metrycznego i trzeba pamiętać, że stosowanie współczesnych jednostek, jak metry czy cale, może nam wprawdzie ułatwić zrozumienie wielkości danej budowli, ale zarazem zaciemnia obraz rzeczywistości historycznej…
Na stronach internetowych, czy też w komentarzach do artykułów publikowanych w internecie, spotkać możemy oburzone wpisy internautów, którzy popierając akademickie poglądy na budowę piramid, są gotowi przyjąć, że Boska proporcja pojawiła się w piramidach nieprzypadkowo... Uważając przy tym, że racjonalizm wymaga choćby wzięcia pod uwagę jakiejś korelacji między liczbą π a liczbą φ... Mają rację...
Do naszej złotej piramidy utworzymy korelacje wzajemne między tymi liczbami π, φ, dodając do tego jeszcze egipski łokieć królewski...
Za łokieć królewski przyjmujemy wartość 1łk = 0,5236 m (według J.H.Cole’a wartość łokcia królewskiego wynosi 0,52375 ± 0,00025 metra). Różnica wynosi 0,00015, a więc mieści się w granicach błędu przyjętego przez J.H.Cole’a. Najbardziej znanym wzorcem łokcia królewskiego jest drewniany wzorzec znaleziony w grobowcu Tutenchamona. Wzorzec ten, obecnie na stałe, znajduje się w galerii poświęconej starożytnemu Egiptowi, w paryskim Luwrze. Wzorzec ten zachowany w bardzo dobrym stanie, wykonany z drewna, ma długość około 0,5236 m. Na wzorcu zaznaczono mniejsze jednostki długości palce (każdemu z palców przyporządkowano imię jednego z bogów egipskich rozpoczynając od boga słońca Ra), dłonie, pięść i piędź, oraz podział palca na mniejsze jednostki od ½ do 1/16.
Możemy zauważyć, nie wnikając w zawiłości matematyczne, że:
1 łokieć królewski = (π/6) metra = 0,523598677...metra.
Wykonanie wzorca łokcia królewskiego wymaga rozwiązania problemu kwadratury koła. Wiemy, że jest to problem trudny do rozwiązania, mamy bowiem do czynienia z liczbą niewymierną. Jak zatem rozwiązać ten problem od strony praktycznej?... Odpowiedź jest tylko jedna... Tak jak robili to starożytni kapłani egipscy...
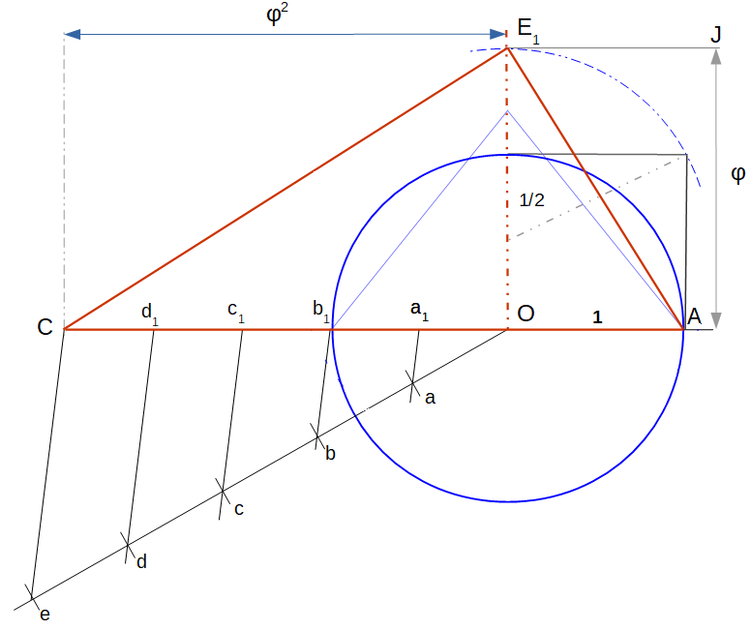
Z własności trójkąta prostokątnego ACE1, o wysokości OE1 = φ mamy:
(OE1)2 = OA × OC stąd: OE1 = (OA × OC)1/2.
Wobec: OA = 1, OE1 = φ otrzymujemy: OC = φ2. Jest bowiem: φ = (1 × φ2)1/2.
Z punktu O rysujemy półprostą na której odcinamy 5 jednakowych odcinków:
Oa = ab = bc = cd = de.
Koniec ostatniego odcinka w punkcie e, łączymy z punktem C. Następnie przez punkty a, b, c, d, prowadzimy równolegle do odcinka eC, do przecięcia się z odcinkiem OC. Otrzymamy 5 odcinków o tej samej długości: Oa1 = ab1 = bc1 = cd1 = d1C.
Długość każdego z odcinków wynosi: (1/5) OC. Wobec OC = φ2(OA) otrzymujemy:
(1/5) OC = (φ2/5) OA = 0,523606798... odcinka OA.
1/12 obwodu okręgu o promieniu OA wynosi: (π/6) OA = 0,523598776... odcinka OA.
Jest więc: (φ2/5) OA≈ (π/6) OA = 1 łokieć królewski.
Różnica wynosi: 0,000002215... długości odcinka OA... Tak więc na każde 100 m odcinka OA błąd jest większy od 2 mm a mniejszy od 2,5 mm; na każdy kilometr błąd jest większy od 2 cm a mniejszy od 2,5 cm...
Jest zatem: φ2 = 2,618033988749880... ≈ (5/6)π = 2,617993878... Różnica wynosi 0,000040110...
Stąd: φ = 1,618033988749890 ... ≈ [(5/6)π]1/2 = 1,618021594... Różnica wynosi: 0,00001239495.
Tak więc udało się nam wyjaśnić wzajemne relacje między liczbami π, φ i łokciem królewskim, relacje, które stosowane w celach praktycznych, w swej prostocie, są po prostu piękne!
Parę zdań o liczbach.
Szczególne znaczenie w starożytnym Egipcie ( i nie tylko) miały liczby 10, 11, 12. Liczba 10 (dekada) była liczbą świętą zarówno u Egipcjan jak i u pitagorejczyków… Liczba 12 związana jest ze świętym trójkątem egipskim i sumą liczb 3, 4, 5. Liczba 11 jest pierwszą z liczb pierwszych większą od liczby 10. Liczba 11 jest większa od 10 a mniejsza od liczby 12. Liczba 11 nie jest liczbą świętą ale liczba ta i jej wielokrotności (22, 44, 88, 176) ma olbrzymie znaczenie. Między świętymi liczbami starożytnych zachodzi relacja:
(12φ2)/10 = (6φ2)/5 = 3,141509 ≈ π.
Underwood Dudley wykazując tą zależność, zwrócił uwagę że w przypadku tych dwóch wartości można mówić o dobrym przybliżeniu (choć niczym więcej). My uważamy inaczej, tym bardziej, że powyższą relację bardzo łatwo wykreślić geometrycznie…
Liczba π i kwadratura koła.
Do anegdot przeszedł słynny pomiar wysokości piramidy dokonany przez Talesa, ucznia kapłanów egipskich, na podstawie długości jej cienia. Pomiar ten świadczy, że zależności zachodzące w wymiarach piramidy nie są przypadkowe i zagadnienie podobieństwa trójkątów nie było obce kapłanom, tym bardziej, że papirus Ahmesa z przed 2 000 lat p.n.e dowodzi, że kapłani potrafili obliczyć objętość stożka ściętego na tysiące lat przed Talesem. Papirus Ahmesa mówi również o tym, że problem kwadratury koła nie był obcy starożytnym Egipcjanom. Według papirusu Ahmesa odrzucając od średnicy koła jego część dziewiątą zbudujemy, na pozostałej części średnicy koła, kwadrat równoważny z kołem...
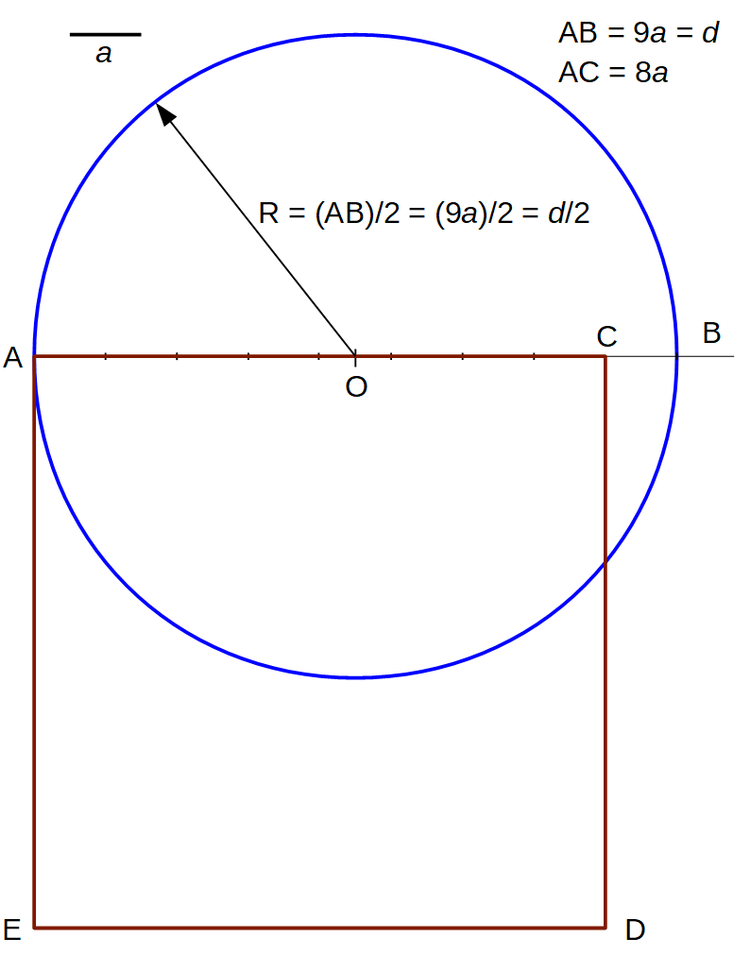
Geometrycznie sposób Ahmesa wykreślamy jak na rysunku powyżej. Zapiszmy jeszcze sposób Ahmesa w sposób współczesny… Średnicę AB koła oznaczymy przez d wówczas wzór na kwadraturę koła będzie postaci:
(d – d/9)2 ≈ π(d/2)2 jest więc: d2 – 2(d2/9) + d2/81 ≈ π(d2/4);
dzieląc obustronnie przez d2 otrzymujemy: 1 – 2/9 + 1/81 ≈ π(1/4). Stąd: 4 – 8/9 + 4/81 ≈ π.
Stąd: (324 – 72 + 4)/81 ≈ π. Ostatecznie otrzymujemy: 256/81 = 3,160493827 ≈ π.
Papirus podaje także przykład praktycznego zastosowania sposobu Ahmesa...
Jaką wartość ma pole powierzchni gruntu w kształcie koła o średnicy 9 khet?
Rozwiązanie:
9/9 khet = 1 khet. Stąd pole wynosi (9 – 1) khet × (9 – 1) khet = 64 khet2.
Oczywiście powiemy, że obliczenie zawiera błąd bowiem mamy:
π(9/2)2 khet2 = 63,61725 khet2
Porównanie wyników daje nam, oprócz wykazania błędu, zastosowane przez starożytnych matematyków przybliżenie liczby π:
π(9/2)2 khet2 ≈ 64 khet2. Stąd: π ≈ (64 × 4)/81 = 256/81 = 3,160493827...
...Czy nasze przybliżenie liczby π = 3,15, dla celów praktycznych, jest lepsze od przybliżenia π = 3,16 stosowane w praktyce przez starożytnych? Należy zwrócić uwagę, że papirus mówi o powierzchni gruntu. Powierzchnia gruntu, zakreślona kołem w przestrzeni, jest zawsze większa od powierzchni koła zakreślonego na płaszczyźnie o tym samym promieniu. Dzieje się tak z uwagi na nierówności, zagłębienia, spadki i wzniesienia występujące na powierzchni gruntów. To kapłani podawali sposoby wyznaczenia powierzchni gruntów dla celów podatkowych... Przybliżenie π = 3,15 daje niedoszacowanie zbiorów, a więc straty dla świątyni i faraona.
Jeszcze uwaga. Nie podaje tytułów publikacji i autorów cytowanych fragmentów tekstu, aby nie być posądzonym o prowadzenie reklamy.
Inne tematy w dziale Technologie

