Efekt motyla - Fiknie czy nie fiknie?

Tak to jakoś w tej całej nauce jest, że choć niby wszystko wiemy, to się tym specjalnie nie przejmujemy, nie dociera do nas. To trochę tak jak z tym Szkotem, co się upiera przy tym, że kilogram stali waży więcej niż kilogram pierza:

Powtarza: ale stal jest cięższa od pierza. A gdy mu pokazują górę pierza i kawałek stali i mówią: jedno i drugie to kilogram, mówi, że go nabierają. Podobnie z nauką. Niby widzieliśmy, że gajka w efekcie Dżabennikowa może fiknąć, ale kiedy naprawdę fiknęła – podniósł się szum. Niby wiemy, że w układach z dynamiką nieliniową dziwne i trudne do przewidzenia rzeczy mogą zachodzić, mamy nawet na to nazwę: „efekt motyla”, ale się tym motylem na co dzień nie przyjmujemy. Mówimy: jutro na pewno będzie takie samo jak dziś. I jest takie samo. Do czasu.

Dziś chcę pokazać najprostszy przykład, przykład który wybrałem śledząc dyskusję pod poprzednią notką Elipsoidalne fikania. W dyskusji tej poruszono istotny wątek, w szczególności bloger KOTIMYSZ zapytał: „Co to znaczy "dowolnie małe" zaburzenie i co to znaczy dla gajki?”

Zajmiemy się tym dzisiaj. W szczególności zobaczymy jak niebezpieczeństwo może się chytrze czaić.

Scenariusz jest ten sam co w poprzedniej notce. Mamy nakrętkę motylkową, jak na tym dobrze już nam znanym filmie

Momenty bezwładności bierzemy 3,2,1. Zaczynamy ją obracać wokół osi ze środkowym momentem bezwładności. Dla nakrętki jest to naturalna oś nakręcania na śrubę. Podobnie jak w poprzedniej notce przyjmiemy, że mamy kręt do kwadratu równy 10 (odpowiednich jednostek):

J² = 10

Energię kinetyczną przyjmiemy

2T_spec = J²/I_Y= 5

Czyli T_spec = 2.5

Przypomnijmy wzory na J² i T:

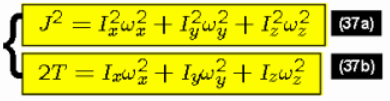
Możemy wybrać rozwiązanie równań Eulera:

ω_X = 0 , ω_Y = √(5/2), ω_Z = 0.

Nakrętka obraca się wokół swej osi – po wieczne czasy! Oto przykładowe wykresy trzech prędkości kątowych:

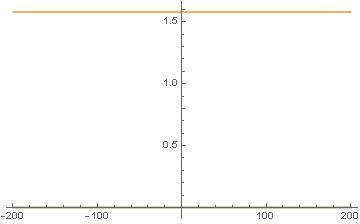
Funkcja stała ω_Y = √5/2 = 1.5811388300841896660...,

i dwie nakładające się na siebie funkcje stałe ω_X = 0, ω_Z = 0.

A teraz przypuśćmy, że zmienię nieco wartości początkowe

 

ω_Y = 1.58113883008418966599944...

ω_X = 7.15351*10^-40

ω_Z = 4.13008*10^-40

Zarówno kręt jak i energia kinetyczna są te same co przedtem – specjalnie tak zrobiłem. ω_X i ω_Y są prawie zerami. Różnią się od zera dopiero na czterdziestym miejscu, coś takiego ...

0.0000000000000000000000000000000000000001..

Takiej różnicy od zera żaden przyrząd pomiarowy nie wychwyci. A jednak. A jednak teraz wykres rozwiązań równań Eulera wygląda tak

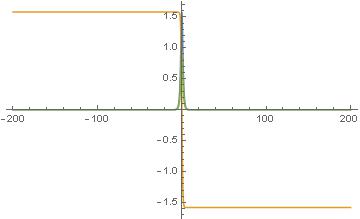
Od niepamiętnych czasów ω_X i ω_Z są praktycznie zerami, ω_Y jest praktycznie stałe. Nakrętka obraca się i obraca i obraca. I nagle przychodzi chwila gdy fika koziołka, tutaj w okolicy t=0. Ni z tego ni z owego ω_Y zmienia znak. To niechybny omen przekoziołkowania. W czasie gdy koziołek się odbywa, chwilowo, ω_X i ω_Z ożywiają się. Potem znów cisza i spokój – po wieczne czasy, tyle, że tyłem do przodu. No, fiknęło mi się, i co z tego? Widział ktoś?

Możemy przyjrzeć się bliżej temu krótkiemu okresowi fiknięcia:

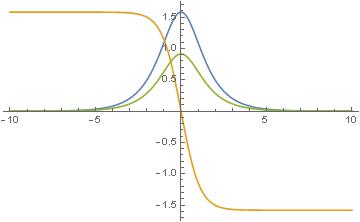
Na wykresie z podręcznika Rubinowicza i Królikowskiego zaznaczyłem odpowiedni fragment trajektorii.

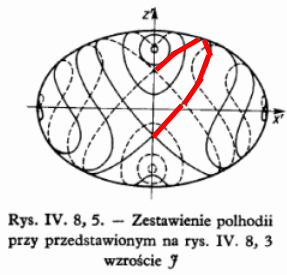
Ona dotyka biegunów, ale bieguny do niej nie należą. Każdy biegun, sam w sobie jest trajektorią. Tyle, że bardzo niestabilną. Lekkie od niego odchylenie, zmiana wartości którejś z prędkości kątowych na czterdziestym miejscu po przecinku, i już nastąpi fiknięcie. Być może długo na nie trzeba będzie czekać, być może nikt się go przez długi czas nie będzie spodziewał, ale niechybnie nastąpi. Po czym, po krótkim okresie tumultu, nastąpi znów cisza, być może po wieczne czasy. A być może nie – diabeł ukrywa się maleńkich, dl oka niewidocznych detalach.

Nie znacie dnia ani godziny!