Kot eliptyczny

Oto mój møodziutki eliptyczny kot, rasa Maine Coon:

Kot tu nie ma nic do rzeczy. Idzie o eliptyczny sinus Jacobiego, funkcję sn(u,m), którą wprowadziłem w poprzedniej notce „Sinus zdeformowany”. Choć, z drugiej strony, ma tu dużo do rzeczy bo akurat leży na moich obliczeniach, na kartkach papieru zapisanych w czasie moich prób zrozumienia czym właściwie są te eliptyczne sinusy i cosinusy

Kot, ściślej kotka, nazywa się „Opal”, a opale bywają eliptycznawe

Co powiedziawszy możemy wrócić do funkcji sn(m,u) z poprzedniej notki. Przypomnę, że mam elipsę z półosiami a>1 i b=1. Parametr m to kwadrat mimośrodu m=1-1/a². Gdy m=0, wtedy a=1 i nasza elipsa jest okręgiem. Możemy jednak naszą elipsę rozciągać coraz bardziej, w granicy gdy a jest nieskończone, wtedy m=1. To są graniczne przypadki. W tych granicznym przypadkach funkcja sn sprowadza się do znanych funkcji

sn(u,0) = sin u

sn(u,1) = tgh(u)

Że sn(u,0) to jest zwykły sinus – to już było w poprzedniej notce. Skąd wziąłem, że sn(u,1) = tanh(u)? Możemy to wyliczyć. W poprzedniej notce mieliśmy

du/dy = 1/√((1-y²)(1-my²)).

Gdy m=1, wtedy po prostu 1/(1-y²). Zaglądamy do tabeli całek i znajdujemy, że całka z tej funkcji po y to arctgh. Zatem u = arctgh y, czyli y = tgh u.

Na wykresach tak to wygląda - w przedziale (-10,10)

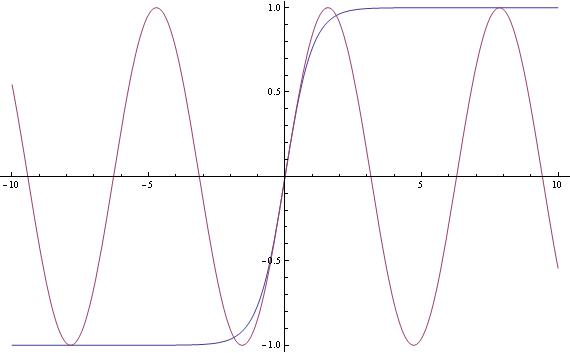
W zastosowaniach do fikających bąków będą nas interesować (jak się wkrótce okaże) przypadki gdy m jest równe 1, lub prawie-prawie równe 1.

Dlatego poniżej podam wykresy sh(m,u) dla m=0.9,0.99,0.999 i 0.9999.

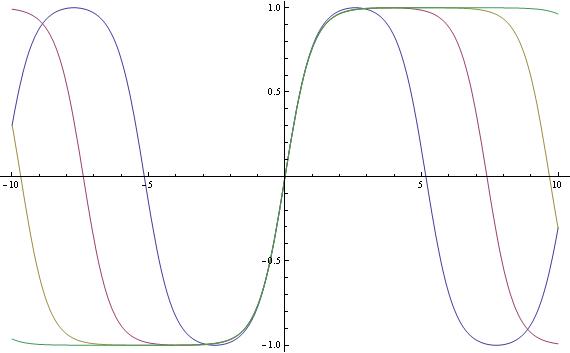
Za każdym razem mamy funkcję okresową, jednak z coraz dłuższym okresem. W granicy, gdy m=1, mamy funkcję z okresem nieskończonym, zatem nieokresową.

Przejście od falistego sinusa do jednofikołkowego hiperbolicznego tangensa odbywa się przez wykresy przebiegów prawie prostokątnych. Dla m=0.999999 wykres wygląda tak

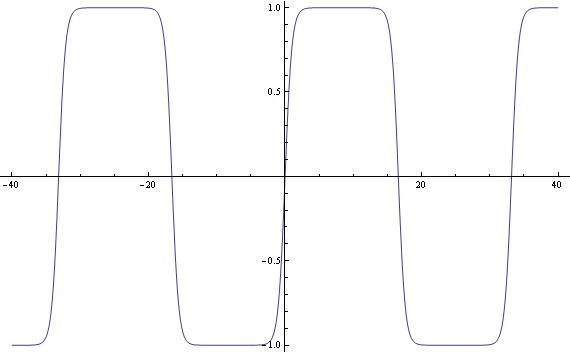
Na osi poziomej jest u, okaże się proporcjonalne do czasu. Te prawie poziome fragmenty, gdy wartość sn(u,m) jest prawie równa +1 lub -1, odpowiadają zwykłemu kręceniu się nakrętki wokół swej osi. Gdy wartość się dość gwałtownie zmienia, z +1 na -1 lub na odwrót, to właśnie fikołki, gdy oś nakrętki się przewraca o 180 stopni. W granicy gdy m=1, mamy w całym życiu nakrętki tylko jeden fikołek. Poza tym jednym fikołkiem normalnie porządnie się kręci, jak na nakrętkę przystało.

Pisząc to, piszę na wyrost, uprzedzam fakty. Na razie po prostu mamy funkcję sn(u,m), którą oswajamy. Na razie bowiem do niczego jej jeszcze nie użyliśmy. A użyjemy jej już wkrótce do jawnego rozwiązania równań Eulera dla bąka asymetrycznego. Od kota tę notkę zacząłem, na kocie ją kończę: