Koty to dziwne są. Tajemnicze. Nieprzewidywalne. O tajemniczym kocie była poprzednia notka Zagadka radioaktywno-statystyczno-paranormalna. Sam kot w notce nie występował. W notce był Cezar i Kleopatra, był Vlad i był Shnoll, był rozpad radioaktywny i była subtelna struktura histogramu. Kot pojawił się dopiero w komentarzach Czytelników: to kot, kot Schrodingera, wpadł przez okno redukując paczkę falową, rezultatem było rozbite akwarium i uśmiercone rybki Kleopatra i Cezar. Normalnie, w mechanice kwantowej układów zamnkniętych, uśmierca się kota. U nas, jako, że mamy układ otwarty, to kot robi za Pana Boga a uśmiercane są rybki. Nie jest jasne jakie to są rybki. Przypuszczam, że z tych złotych. Przeczytałem właśnie, że na skutek współczesnych technologii i zgiełku informatycznego człowiek oduczył się koncentracji uwagi. Badania wykazały, że dzisiejszy obywatel jest w stanie skoncentrować uwagę średnio przez 9 sekund, nie więcej. Co jest akurat ile wynosi średni czas koncentracji uwagi złotej rybki.
Proponuję zatem ćwiczenie: koncentrację uwagi na symulacji rozpadu radioaktywnego. I nie jest to żart (a może jest?).
Jest mianowicie biolog Simon Shnoll. Że jest – w to nie należy wątpić. Jest przecież w Wikipedii. Według Wiki jest to biofizyk, jest profesorem na Wydziale Fizyki Uniwersytetu Moskiewskiego, nauczał wielu znanych badaczy. Interesuje go szczególnie czas i zjawiska oscylacyjne. Jest autorem ponad 200 publikacji, wypromował 70 doktorów. Wśród wymienionych w Wiki publikacji mamy: S. Shnoll Cosmophysical factors in random processes . - Stockholm (Sweden): Svenska fysikarkivat, 2009. - 388. - ISBN 978-91-85917-06-8 – wymieniałem ją w poprzedniej notce.
A gdzie kot? - zapytasz.

Cierpliwości. Zaraz na scenie zjawi się i kot. Otóż, jak to pisałem w poprzedniej notce, nasz bohater rejestrował zdarzenia rozpadu radioaktywnego i przyglądał się bacznie histogramom. W tych histogramach widział to, czego inni nie widzą – jak to zwykle jest z geniuszami. A że kot ukrywa się detalach – zajmijmy się tymi detalami. Na początek weźmiemy na tapetę ten histogram Shnolla z poprzedniej notki.
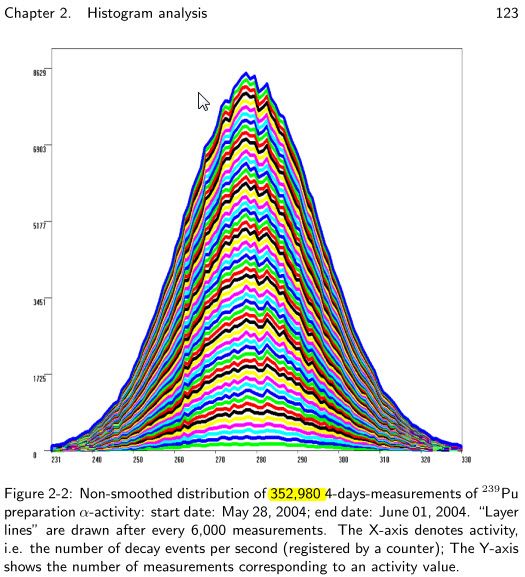
Shnolla interesuje ta systematyczna pagórkowatość na prawo od maksimum – nazywa to strukturą subtelną. Opiszę teraz jak ja ją zasymulowałem niechcący na komputerze.
Shnoll pisze, że obserwował rozpad izotopu Plutonium Pu 239 przez 4 doby, że średnio było 279 zarejestrowanych rozpadów na sekundę. No to rachuję:
4 x 24 x 3600 x 279 = 96 422 400
Tyle mniej-wiecej zdarzeń jego detektor zarejestrował. Mój komputer musi więc wygenerować 100 mln takich zdarzeń przy użyciu generatora liczb losowych. No, ściślej pseudo-losowych, bo czy generatory liczb naprawdę losowych istnieją – to jest duży znak zapytania. Ma to symulować rozpad radioaktywny czyli rozkład Poissona. Można znaleźć w sieci algorytm jak się to robi. Oto jak ja to zrobiłem.
Najpierw generuję listę 100 mln liczb przypadkowych z przedziału (0,1). Uzywam programu Mathematica, załatwia mi to komenda:
rnd = RandomReal[{0, 1}, 10^8];
Na moim PC trwa to ok 4 sekundy. Wygenerowane liczby wyglądają jakoś tak
0.242791, 0.525942, 0.202287, 0.123214, 0.685237, 0.295718, 0.720473,
0.546506, 0.85375, 0.365829,....
I jest ich 100 milionów.
Teraz stosuję trick znany statystykom, by z tego rozkładu równomiernego wygenerować rozkład Poissona ze średnią liczbą 279 zdarzeń na sekundę. Uzywam zatem listy rnd i buduję z niej nową listę, nazywam ją poi
L = 279
poi = -Log[1.0 – rnd]/L;
Ta nowa lista ma też 100 mln liczb
0.000996833, 0.00267536, 0.000810058, 0.000471299, 0.00414314,
0.00125655, 0.00456866, 0.00283431, 0.00689045, 0.00163239, …
To są odstępu pomiędzy kolejnymi rozpadami. Muszę teraz posumować by dostać czasy kolejnych rozpadów:
0.000996833
0.000996833+0.00267536
0.000996833+0.00267536+ 0.000810058
….
Załatwia mi to komenda Accumulate
pois = Accumulate[poi];
Otrzymuję listę czasów kolejnych rozpadów (dalej mam 100 mln)
0.000996833, 0.0036722, 0.00448225, 0.00495355, 0.0090967, 0.0103532,
0.0149219, 0.0177562, 0.0246467, 0.0262791,...
Sprawdzam ostatnią liczbę w tej liście:
358448.
Czyli moje zdarzenia zajmują 358449 sekund. Nieco ponad 4 doby, bo 4 doby to 4x24x3600=345600 sekund. Zatem mniej-więcej pasuje do doświadczenia.
Teraz muszę zrobić nową listę o 358449 elementach. Muszę policzyć ile zachodzi zdarzeń w każdej kolejnej sekundzie. Tu przydałby się jakiś sprytny programista, bo ja, niestety, umiem to robić tylko „na pałę”, a to zajmuje dużo czasu. Oto jak ja to robię bez sprytu i umiejętności programisty, w języku Mathematica:
s = ConstantArray[0, 358399];
Tworzę listę 358399 zer, następnie ją wypełniam
Do[s[[1 + Floor[pois[[i]]]]]++, {i, 100000000}]
To jest wąskie gardło mojego algorytmu. Przejście 100 mln liczb, jedna pod drugiej, sprawdzenie w której sekundzie zdarzenie zachodzi i zwiększenie licznika dla tej sekundy o 1 – zajmuje 5 minut. Przy umiejętnym programowaniu i skompilowaniu powinno to trwać 5 sekund lub mniej – tak sądzę.
Moja nowa lista s wygląda tak
264, 269, 260, 271, 269, 256, 289, 278, 284, 257,...
Są to ilości zdarzeń (zarejestrowanych rozpadów) w kolejnych sekundach. A tych sekund – przypomnę – było 358399. Widać, że ilości zdarzeń w kolejnych sekundach oscylują bezładnie wokół średniej, a ta średnia jest gdzieś koło 279.
Teraz, tak jak to robi Shnoll, dzielę moją listę na podlisty po 6000 sekund. Będzie ich 59:
ss = Partition[s, 6000];
Teraz krok kolejny, właściwie ostatni w tym naszym doświadczeniu. W każdej podliście trzeba zliczyć ile było sekund z 0 zdarzeniami, ile z 1 zdarzeniem, … ile z 230 , ile z 280, ile z ….
Skoncentruję się na zliczaniu sekund ze zdarzeniami od 230 do 330 – jak to jest na rysunku u Shnolla. Robię to tak:
Tworzę pustą listę t, następnie wypełniam ją kolejno listami z liczbą sekund z liczbą zdarzeń od 230 do 330.
t = {};
For[j = 1, j < 60, j++,
AppendTo[t,Table[Count[ss[[j]], u_ /; i - 1 <= u < i], {i, 230, 330}]]];
Po czym akumuluję:
tt=Accumulate[t];
I to już wszystko. A teraz robię wykresy
ListPlot[Table[tt[[i]], {i, 1, 59}], DataRange -> {230, 330},
Joined -> True]
No i wychodzi coś całkiem podobnego do tego wykresu u Shnolla. On dostał ten wykres używając kota redukującego paczki falowe, my dostaliśmy przy użyciu kota inteligentnego i bezpiecznego, kryjącego się w algorytmie generacji liczb losowych.
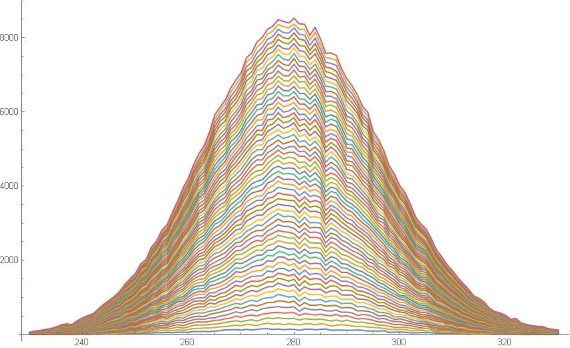
Shnolla „struktura subtelna” widoczna jest jak na dłoni. A czy kryje się w niej jakaś informacja? Informacja o czym? Nad tym warto pomyśleć, bo tam się para Nobli kryć może.








Komentarze
Pokaż komentarze (70)