MM&AlK
W wielu publikacjach popularnonaukowych, stronach internetowych i filmach spotkamy się z fascynacją piramidami, a w szczególności piramidą Cheopsa – tą starożytną budowlą, będącą ostatnim zachowanym cudem świata starożytnego. Na łamach prasy, filmów mówiących o starożytności, trwają spory dotyczące wymiarów piramidy. Jedni podkreślają, że stosunek połowy obwodu piramidy do jej wysokości jest liczbą pi, inni mówią, że to przypadek bo można stwierdzić dokładność tylko do dwóch miejsc po przecinku... Trwają spory o dokładność pomiarów, o jednostki przeliczeniowe, o stosowane przez starożytnych wzorce miar (jednostek), o to czy w wymiarach mamy do czynienia ze złotą liczbą, czy też nie… Aby nie włączać się w ten nurt polemiki zaprojektujemy własną piramidę… ZŁOTĄ PIRAMIDĘ.
Złota liczba, Boska proporcja, złote cięcie...
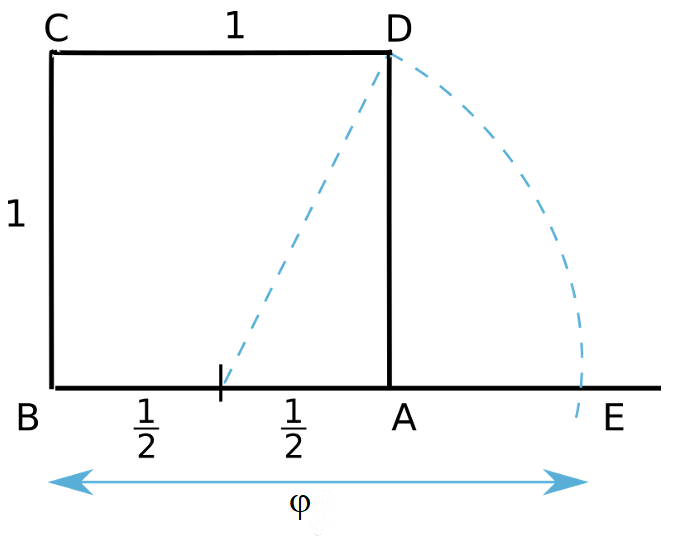
Tak jak w matematyce, mechanice, optyce i naukach pokrewnych twierdzenie Pitagorasa odgrywa podstawową rolę, tak w przyrodzie, architekturze i sztuce podstawowe znaczenie, w starożytności i wiekach średnich, miało złote cięcie (boska proporcja). Złote cięcie, to podział odcinka na dwie części tak, że stosunek całego odcinka do swej części większej, ma się tak, jak większa część do mniejszej. Nazwę boska proporcja, takiemu podziałowi odcinka, nadał mnich Fra Luka Pacioli z Borgo, poświęcając tej proporcji wspaniały traktat Divina Proportione, wydany w Wenecji w 1509 r. Ilustracje do tego traktatu rysował przyjaciel mnicha, sam Leonardo da Vinci. Z boską proporcją związana jest złota liczba. Jest to jedna z najsławniejszych liczb matematyki... Złotą liczbę otrzymamy rozwiązując równanie kwadratowe w postaci:
x2 – x – 1 = 0.
Pierwiastki równania kwadratowego wyniosą: x1 = (1 + 51/2)/2, x2 = (1 – 51/2)/2
Dodatni pierwiastek ma wartość: x1 = φ = (1 + 51/2)/2 = 1,618033988749...
Jest to złota liczba. Dla złotej liczby, po podstawieniu jej do równania kwadratowego, zachodzą zależności:
φ2 – φ – 1 = 0 stąd: φ2 – φ = 1.
Dzieląc obustronnie przez φ mamy: φ – 1 = 1/φ ; stąd: φ – 1/φ = 1 ; φ = 1 + 1/φ
Dla n-tej potęgi złotej liczby zachodzi zależność: φn = φn – 1 – φn – 2.
Złotą liczbę wykreślimy geometrycznie jak na rysunku poniżej.
Złoty piramidon.
W Wikipedii przeczytamy, że Piramidion (Benben), to kamień wieńczący szczyt piramidy lub obelisku, będący miniaturą piramidy właściwej z zachowaniem jej proporcji. W Starym Państwie pokrywany był złotem lub elektronem.
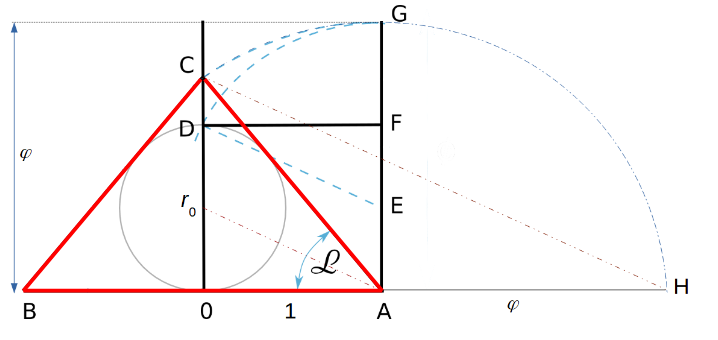
Z rysunku powyżej (z przekroju piramidionu, gdzie "1j" jest przyjętym wzorcem długości) otrzymujemy:
OA = AF = 1/2 boku podstawy piramidionu = 1j, AE = 1/2 boku AF = 1j/2,
AC = AG = wysokość ściany bocznej piramidionu = φ × 1j, OC = h.
Wysokość piramidionu wynosi:
h2 = φ2(1j)2 ₋ (1j)2 = (1j)2(φ2 ₋ 1) stąd: h = (1j)(φ2 ₋ 1)1/2
wobec: (φ2 ₋ 1)1/2 = φ1/2 mamy: h = (1j) × φ1/2.
Stosunek wysokości piramidionu do 1/2 długości podstawy: h/(1j) = φ1/2.
Stosunek obwodu podstawy piramidionu do podwojonej wysokości piramidionu wynosi:
8j/2h = 4j/h. Wobec: h = (1j) × φ1/2 mamy: 4j/(1j × φ1/2) = 4/φ1/2 = 3,1446.
Kwadrat wysokości piramidionu wynosi: h2 = (1j)2 φ.
Pole powierzchni ściany bocznej wynosi: ps = (2j × 1j × φ)/2 = (1j)2φ.
Stąd: Stosunek powierzchni ścian bocznych piramidy do pola powierzchni podstawy wynosi:
(4ps)/4(1j)2 = φ.
Kwadrat wysokości piramidionu jest równy polu powierzchni ściany bocznej: h2 = ps.
Grecki historyk Herodot (ok. 485 - 424 r. p.n.e.) twierdził, że piramida Cheopsa w Gizie została zaprojektowana tak, by kwadrat jej wysokości był równy powierzchni jednej ze ścian bocznych i... Jeśli Herodot ma rację, to piramida Cheopsa była projektowana jako złota piramida...
Stosunek promienia r0 kuli wpisanej w piramidon (okręgu wpisanego w przekrój piramidionu) do 1/2 długości podstawy wynosi:
r0/(1j) = φ1/2/(φ + 1).
Otrzymujemy więc odpowiednio:
Promień r0 kuli wpisanej w piramidion (okręgu wpisanego w przekrój piramidionu):
r0= [φ1/2/(φ + 1)] × (1j).
Kąt a nachylenia ściany bocznej:
Wobec h/(1j) = φ1/2 = tg α = 1,2720 mamy: α = 510 50’ ≈ 2 × 260.
Kąt nachylenia dwusiecznej kąta α/2:
Wobec r0/(1j) = φ1/2/(φ + 1) = tg α/2 = 0,48586841... mamy: α/2 = 25055’ ≈ 260.
Mamy również: h/φ = φ1/2/φ = 1/φ1/2 = sin α ; 1/φ = cos α ; stąd: sin2 α + cos2 α = 1/φ + 1/φ2 = 1.
Jest bowiem: 1/φ + 1/φ2 = 1 ; stąd po obustronnym wymnożeniu przez φ2 otrzymujemy:
φ + 1 = φ2 ; zatem: φ = φ2 – 1.
Piramidion jest tylko modelem piramidy zasadniczej. Jak projektować bryłę piramidy i lokalizację komór o tym w kolejnych notkach...
Inne tematy w dziale Technologie

