Wczoraj przyszła jeszcze jedna z zamówionych książek: „Tako rzecze Sedlak” Kazimierza Dymela. Przyszła z antykwariatu, o dziwo nawet z własnoręcznym autografem autora. Sedlaka uwielbiam, wiele razy pisałem, że to mój wzór i bohater – przykład do naśladowania. No bo jak nie naśladować?
„Moja najpierwsza życiowa maksyma brzmi: jeśli gra – to o najwyższą stawkę, jeśli ryzyko – to zupełne, jeśli szaleństwo – to absolutne.”
Przy całym moim uwielbieniu dla Sedlaka nie wszystko jednak potrafię sobie przyswoić. Na przykład Sedlak raz po raz podkreśla, że wszystko nad czym pracuje zawdzięcza sobie i Bogu. Przede wszystkim Bogu. Szkoły, studia, książki niczego go nie nauczyły. Od zagranicy niczego się uczyć nie należy, to zagranica winna się uczyć od nas.
Ze mną jest inaczej. Ja co i rusz podkreślam, że uczyć się trzeba przez całe życie, choćby i od diabła, angielski trzeba znać, książki studiować, że lepiej wiedzieć niż nie wiedzieć, że trzeba stawać na ramionach olbrzymów – wtedy widzi się dalej.
Z Wikipedii:
W jednym z listów do Hooke’a z datą 5 lutego 1676 Newton napisał: „Jeśli widzę dalej, to tylko dlatego, że stoję na ramionach olbrzymów”.
I tak jest z gajką Dżanibekowa – problemem, którym się zainteresowałem nie wiem dlaczego (Bóg mi go wskazał?). Miast rozwiązywać problem samemu od samego początku zapoznawałem się najpierw ze wszystkim co inni dotąd na ten temat wypracowali. Dziś, w dobie internetu, nie jest to takie trudne przedsięwzięcie. Oczywiście potrzebne są tu dobre podstawy matematyczne, ale, dzięki Bogu, moje studia zmusiły mnie do ich opanowania. Sedlak na matematykę narzekał, pewnie dlatego, że takich podstaw nie miał. Oczywiście wiem, nadmiar wiedzy nie zawsze jest dobry, czasem lepiej nic nie wiedzieć, na przykład, nie wiedzieć, że „coś jest niemożliwe”. Sedlak podkreślał, że lubi zabierać się przede wszystkim za rzeczy niemożliwe. To u niego lubię. To kupuję!
Z tą fikającą gajką najbardziej pomogła mi praca
Ramses van Zon, Jeremy Schofield, "Numerical implementation of the exact dynamics of free rigid bodies", J. Comput. Phys. 225, 145-164 (2007)
Autorzy niby rozwiązują tam problem niesymetrycznego bąka, jednak mi się ich rozwiązanie nie podoba, więc wziąłem od nich to co mi się podobało, a dalej poszedłem już inną drogą. Piszą tak:
„Podczas gdy problem rozwiązywania równań Eulera w układzie związanym z ciałem jest dość pospolity, mało kto dyskutuje jak rozwiązać równania dla macierzy orientacji.”
Autorzy piszą „mało kto”, ale nie cytują nikogo. Jest to więc przypuszczalnie eufemizm. Chcieli pewnie powiedzieć „nikt” zamiast „mało kto”, ale napisać mało kto jest bezpieczniej, łatwiej przejdzie przez recenzentów.
No i się za rzecz zabierają. I początek mają świetny. Jednak potem jakoś kluczą. W rok potem pojawiła się inna publikacja na ten sam temat:
Celledoni, Elena; Zanna, Antonella.E Celledoni, F Fassò, N Säfström, A Zanna, The exact computation of the free rigid body motion and its use in splitting methods, SIAM Journal on Scientific Computing 30 (4), 2084-2112 (2008)
Piszą ci autorzy, że „w ostatnich latach zainteresowanie problemem się odrodziło”. No i problem, ich zdaniem, rozwiązują. Co nie przeszkodziło temu by w roku 2012 pojawiła się nowa praca
Marcello Romano, "Concise Form of the Dynamic and Kinematic Solutions of the Euler-Poinsot Problem", Advances in the Astronautical Sciences Volume 145, (IAA-AAS-DyCoSS1-01-05), (2012)
Autor cytuje poprzedników, jednak narzeka, że wciąż brak jasności i proponuje swoją alternatywę. Jak dla mnie – najmniej jasną.
Ja biorę co mi pasuje, przerabiam po swojemu. Trochę tak jak to artyści kradną idee jeden od drugiego, czasem się do tego przyznając, częściej jednak robią to nieświadomie. To o czym dziś napiszę pochodzi od van Zona i Shofielda – w takim wydaniu jak ja to przetrawiłem.
Co mamy? Ano mamy kręcącą się i fikającą skrzydlatą nakrętkę
Chcemy opisać jej zachowanie, wymodelować przy użyciu znanych od dawna równań mechaniki klasycznej, tych wywodzących się jeszcze od Newtona i od Eulera. Ze znanych parametrów chcemy wymodelować ruch, taki jak ten obserwowany w doświadczeniu. Gdy nam się taki opis uda, będziemy mogli użyć naszej wiedzy w procesie odwrotnym – z obserwacji ruchu wnioskować o parametrach, z obserwacji ruchu dowiadywać się czegoś o przyrodzie. Zwykle najpierw jakieś zjawisko obserwujemy, gdy już opanujemy rządzące zjawiskiem prawa, wtedy znajdujemy dla zjawiska zastosowanie. Tak jak na przykład z termometrem. Najpierw zaobserwowano, że rtęć się ze wzrostem temperatury liniowo rozszerza, potem użyto tego rozszerzania do pomiaru temperatury. Co możemy mierzyć obserwując fikanie? Jestem pewien, że tego rodzaju niestabilne zjawisko, czułe na parametry, wcześniej czy później znajdzie jakieś zastosowanie. A co jeśli znajdziemy związek częstotliwości fikania z trzęsieniami Ziemi? Z porami roku?
Mamy więc fikającą gajkę (to nowotwór językowy, to ruszczyzna, mamy skrzydlatą nakrętkę).

Do gajki przymocowujemy (wystarczy, że w myślach) układ współrzędnych (x',y'z'). Najmniejszy moment bezwładności względem osi x', największy względem osi z'. Ten układ współrzędnych wiruje i fika razem z gajką. Tak to widzimy z układu laboratoryjnego (x,y,z). Mechanika Newtona i Eulera mówi nam, że jeśli nasz układ laboratoryjny jest układem inercjalnym, wtedy istnieje w całym tym fikaniu wyróżniony stały wektor – to wektor krętu. Tego wektora nie widzimy, widzimy wirowanie i fikanie. Niemniej on jakoś w przestrzeni jest, choćby i po platońsku, potencjalnie. Ten tajemniczy niewidzialny wektor krętu, stały względem laboratoryjnego układu współrzędnych, jest kluczem do zrozumienia zachowania się gajki. Choć go nie widzimy, wiemy, że jest. Nic więc nie stoi na przeszkodzie byśmy sobie założyli, że jest on ustawiony wzdłuż osi z laboratorium. W razie czego zawsze możemy osie w laboratorium spróbować obrócić tak, by się tak stało. I tak będziemy zakładać. W układzie wirującym (x',y',z') wektor L ma składowe (L1,L2,L3), zależne od czasu. Rozwiązanie równań Eulera daje nam zależności L1(t),L2(t),L3(t). Skalę czasu wybieramy tak, by długość tego wektora była równa 1. W układzie (x,y,z) wektor ten ma zatem składowe (0,0,1).
Związek pomiędzy tymi dwoma układami dany jest macierzą transformacji (patrz poprzednia notka)
r(t) = Q(t)r'
Q(t) jest tu macierzą ortogonalną 3x3. Gdy tą macierz znajdziemy, będziemy w stanie narysować jak wygląda kręcenie się i fikanie widziane z laboratorium – podobnie jak to widzimy na filmie zrobionym na pokładzie stacji kosmicznej. O macierzy Q(t) wiemy, że spełnia równanie różniczkowe
dQ(t)/dt = Q(t) W( w' (t) )
gdzie W( w' (t) ) jest macierzą
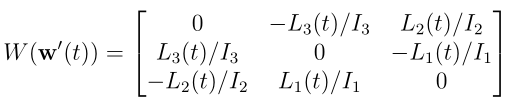
Jeśli zadamy Q(t) dlat t=0, wtedy twierdzenie o istnieniu i jednoznaczności zapewnia nam, że nasz układ równań różniczkowych na dziewięć współczynników macierzy Q(t) ma rozwiązanie, i to dokładnie jedno. Jesli Q(t) jest rozwiązaniem, zaś R jest dana macierzą ortogonalną, wtedy RQ(t) jest też rozwiązaniem - i to jest cała dowolność. Jest to dowolność ustalenia orientacji laboratoryjnego układu współrzędnych. Gdy będzieli znali jedno rozwiązanie, będziemy w zasadzie znali wszystkie. Jednak znalezienie jakiegoś rozwiązania do nas należy. Można co prawda rozwiązywać na pałę numerycznie, jednak wtedy błędy będą narastały z czasem, w dodatku trudno wtedy zapewnić ortogonalność w ten sposób wyliczonej macierzy Q. My chcemy mieć rozwiązanie jawne, zapisane formułą. Nadzwyczaj niewygodnie jest mieć do czynienia z układem dziewięciu równań. Jeżeli jednak użyjemy naszych danych oraz naszej intuicji i wyobraźni geometrycznej, wtedy można cały problem znalezienia rozwiązania zredukować do jednej tylko całki. Tak właśnie robią van Zon i Shofield. A ja się od nich nauczyłem.
No bo tak: mamy dwa układy odniesienia i wektor L. W jednym układzie ten wektor ma składowe (L1,L2,L3), a w drugim (0,0,1). To za mało informacji by znaleźć przejście od jednego układu do drugiego, ale to wystarczająca informacja by problem znacznie uprościć. Sztuczka polega na tym by przedstawić Q jako złożenie dwóch transformacji. Pierwsza transformuje układ związany z ciałem tak by ustawić trzecią oś układu (x',y',z') wzdłuż wektora L „siłą, na pałę”. Potem już zostaje prosty obrót w płaszczyźnie prostopadłej do trzeciej osi by otrzymać całe Q. Zapisujemy więc
Q(t) = Q1(T) Q0(t)
gdzie
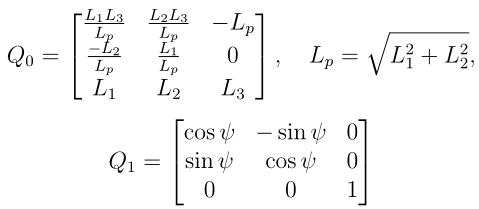
Można sprawdzić, że Q0(t) z samej konstrukcji jest macierzą ortogonalną i że Q0 w działaniu na wektor o składowych (L1,L2,L3) automatycznie daje wektor o składowych (0,0,1) – przypomnę, że wektor L ma u nas długość 1. W formułach powyżej opuściłem zależność od czasu t. Zależność od czasu L1,L2,L3 jest znana – z rozwiązania równań Eulera. Zostaje więc jedyni znalezienie zależności od czasu kąta psi. Podstawiamy powyższe Q(t) do równania na dQ(t)/dt, trochę mechanicznego liczenia, i wyskakuje równanie różniczkowe na psi(t).
Otrzymanie tego równania i jego rozwiązanie będzie niejako uwieńczeniem naszej wirującej i fikającej przygody. Będziemy mogli już wtedy ze znajomością rzeczy rozprawiać "O obrotach ciał niebieskich". Zostanie już tylko przyglądaniu się rozwiązaniom i wyciąganie wniosków.
Tak to już jest, że w nauce jest czas i miejsce na ogólne idee, ale jest też czas i miejsce na techniczne prace. Modlił się ks. prof. Włodzimierz Sedlak:
„Daj mi o Panie Boże, a z warczeniem burzy wyrżnę jasnym piorunem w sam środek kołtuństwa, by należycie nim potrząsnęło.”
Do tego kołtuństwa zaliczał niewątpliwie Sedlak tych „zwykłych naukowców”, takich jak ja, co to równania rozwiązują. Pozostaje chyba zgodzić się z posłowiem Ks. Prof. Napiórkowskiego do Sedlaka „Teologii Światła”:
„Razi trochę niebotyczne mniemanie Autora o swoim dokonaniu (porównanie z Kopernikiem – przechyla na swoją stronę – roz. 1), jeśli jednak akceptujemy styl ks. Sedlaka i bardzo osobisty ton przyjęty w książce, nie trzeba protestować.”







Komentarze
Pokaż komentarze (23)