Rozmywanie i wyostrzanie

Ta notka wystaje z cyklu. A to dlatego, że BJAB zadał, w komentarzu pod ostatnią notką, pytanie z dziedziny obróbki obrazków. Ja odpowiedzieć nie potrafiłem. W komentarzach tych co się na problemie znają padło kilka ciekawych uwag, jednak dość powierzchownych, zapewne z braku czasu. Mnie problem zainteresował, zacząłem go studiować pod różnymi kątami. W końcu odpuściłem transformaty Fouriera i skoncentrowałem się na samym tylko problemiku. Tak by można było rzecz zrozumieć i samemu wszystko wyrachować przy pełnej kontroli tego, co robimy. I oto mój wynik.

Problem postawiony przez BJABA wyglądał tak:

Mam problem matematyczny (algebraiczny?) dotyczący informacji.
Niech będzie zdjęcie (obrazek, pejzaż, portret) komputerowe. Ostre. Dla uproszczenia niekolorowe - w odcieniach szarości.
Modyfikujemy to zdjęcie. Rozostrzamy je (komputerowo).
Jak? -
Starą wartość każdego piksela zastępujemy jakąś nową wartością (jakąś średnią ważoną starej wartości piksela i starych wartości czterech(?) sąsiednich pikseli).
Czy tak powstałe zdjęcie, rozostrzone, zawiera tyle samo informacji co stare?
Czy można z tego nowego zdjęcia odtworzyć (idealnie?) stare, ostre zdjęcie?

Można to potraktować jako rozmywanie obrazka filtrem liniowym, który można schematycznie przedstawić jako macierz 3x3

0 1/5 0

1/5 1/5 1/5

0 1/5 0

Szarość każdego pikselka zastępujemy średnią z niego, i z tego co obok, na prawo i na lewo, na górze i na dole. W przykładach w literaturze zazwyczaj albo w samym środku mamy zero a zamiast pozostałych 1/5 mamy 1/4, albo mamy wszystkie 9 elementów różne od zera i równe, każdy 1/9. Takie filtry służą zwykle do usuwania przypadkowych zaburzeń z obrazka typu czarna kropka czy biała plamka, ni z tego ni z owego. Oczywiście brzegi elementów na obrazku się przy tym nieco rozmywają. Do uwydatniania brzegów używa się specjalnych, innych filtrów.

W praktyce pojawia się problem co robić z pikselami na brzegu obrazka. Bo na lewym brzegu nie ma już piksela na lewo on niego. Różne są możliwości, rachunkowo dość proste jest założenie, że obrazek jest kawałkiem okresowej powtarzającej się mozaiki. Zatem na prawo od ostatniego prawego piksela jest pierwszy lewy piksel itd. itp. Do zastosowań praktycznych jest to założenie dość głupie, jednak wystarczające dobre by z istotą problemu się zapoznać. Łatwiej się wtedy programuje.

W praktyce grafiki komputerowej tego typu problemy załatwia się zwykle używając szybkiej transformaty Fouriera. Inaczej, gdy się robi na palcach, rachunki są koszmarne, czasochłonne. Ja jednak chcę robić na palcach. By tak móc robić ograniczyłem się do obrazka 16x16 pikseli. Moim obrazkiem wyjściowym jest prosta szachownica, tyle, że 16x16 a nie 8x8 jak zwykle. W powiększeniu obrazek wyjściowy wygląda tak:

Fig. 1

 

Nasza szachownica ma 16x16=256 pól. W każdym polu mamy stopień szarości, u mnie jest to liczba między 0 a 1. W moim konkretnym przypadku w każdym polu oryginalnego obrazka stoi albo 0 ( kolor czarny) albo 1 (kolor biały).

Nasz obrazek można zatem traktować jako wektor w 256-wymiarowej przestrzeni. Wiem, że są ludzie co się boją większej liczby wymiarów niż 3. W grafice komputerowej pracujemy w przestrzeniach o milionach wymiarów, i specjalnie w tych przestrzeniach straszno nie jest!

Nasza operacja rozmywania jest liniowa. Daje się zapisać jako działanie macierzy 256x256 na nasz wektor o 256 składowych (szachownica). Z macierzy do wektora przechodzimy prosto, pisząc kolejno, jeden za drugim, wiersze macierzy.

Gdy to wszystko zapiszemy wzorami, łatwo dostaniemy macierz 256x256 opisującą BJABOWą operację rozmywania. Jest to macierz z samych zer, tylko tu i ówdzie stoi 1/5 zamiast zera. Różne od zera elementy tej macierzy stoją w pobliżu przekątnej. Schematycznie nasza macierz rozmywająca wygląda tak:

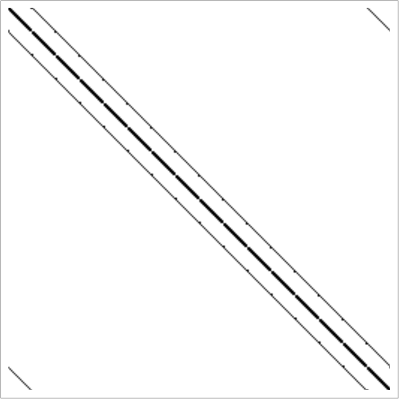
Fig 2

Jak widać są tam też elementy z dala od przekątnej, a to ze względu na nasze warunki periodyczności.

Operację rozmywania można teraz wykonać tak. Rozwijamy szachownicę w długi wektor. Działamy na ten wąż naszą macierzą. Zwijamy wynik znowu w macierz. Oto wynik:

Fig 3

Widzimy, że lewy górny piksel, co najpierw był czarny, zrobił się jasno szarawy. Nic dziwnego. Bo był otoczony czterema białymi i przy uśrednianiu białość przeważyła.

Pojawia się teraz pytanie BJABa: czy ta operacja jest odwracalna?

W naszym przypadku sprowadza się do tego, czy nasza macierz 256x256 jest odwracalna? Wyznacznik można policzyć, choć wynik nie jest zachęcający. Wynosi

(3982621940737800157885559238963 / 172723371101888892507727037256007991422320007
28872562770047406940337183606324854115943015006944576453121094587892299327193
990197893663893387306007554116149549372494220733642578125)

Niewiele nam to mówi. Więc zamieniamy to na liczbę rzecywistą. W przybliżeniu jest to -2.30578*10^-148. Liczba różna od zera, ale bardzo, bardzo, bardzo mała. Operowanie liczbami ze 148 znakami po przecinku może lekko prowadzić do błędów numerycznych. (Nie jest to prawdziwy problem, bowiem w naszym przypadku całą macierz można pomnożyć przez 5 i uwzględnić tę piatkę potem). Niemniej macierz odwrotną można wyrachować. Jej struktura jednak jest bardziej skomplikowana niż struktura macierzy rozmywającej. Mianowicie, schematycznie, tak to wygląda:

Fig 4

Działanie macierzy odwrotnej na rozmyty obrazek reprodukuje dokładnie wyjściową szachownicę. Zatem odpowiedź na pytanie BJABa jest: nie tracimy informacji – przynajmniej w teorii.

Jednakże popatrzmy co się będzie działo gdy do rozmytego obrazka zakradnie się jakiś szum.

Fig 5

Jeśli podziałamy odwrotną, wyostrzającą macierzą na ten zaburzony rozmyty obrazek, otrzymamy:

Fig 6

Oryginał został odtworzony w sposób bardzo bardzo kiepski. Operacja wyostrzania jaką tu zastosowaliśmy, choć teoretycznie poprawna, jest niestabilna. W praktyce, gdy źródłem rozmycia jest na przykład kiepskie ogniskowanie, gdy nawet mamy na to formułę, do wyostrzania nieostrych fotografii używamy skuteczniejszych, bardziej nieczułych na szumy, bardziej stabilnych metod. Lepiej mniej dokładnie, ale pewniej, niż w stu procentach dokładnie ale niestabilnie, z nie mającymi nic wspólnego z rzeczywistością artefaktami.