Azrael to kot. To znaczy na początku, w komiksach, to była kotka. Potem w kreskówkach z kotki zrobił się kot. I tak już zostało w dalszych komiksach. Według angielskiej Wikipedii z zawodu jest kotem, ukierunkowanym ku złu. Służy Gargamelowi, jak rozumiem Gargamel to zły czarownik.

Złych czarowników to owszem, w polityce nie brakuje. Złych kotów też. Smerfy mają ciężkie życie. Czytam jeszcze w tejże Wikipedii, że
„The name Azrael is derived from an Angel of Death in Judaism, Christianity, Islam and Sikhism faiths. The name literally means "Whom God Helps", in an adapted form of Hebrew.”
Imię Azrael wywodzi się od Anioła Śmierci w Judaizmie, Chrześcijaństwie, Islamie i w wierze Szyitów. W przyjętej formie hebrajskiego oznacza dosłownie „Ten, któremu Bóg pomaga”.
No ja dziękuję za taką pomoc. Ale, ale. Wczoraj mało nie umarłem. Otóż, od jakichś dwóch lat dobiera mi się do kości „ząb mądrości”. Nic nie pomaga tłumaczenie, że jakby trochę późno, że wszystkie miejsca zajęte. Od czasu do czasu się aktywizuje i chce wysadzić pół mojej szczęki w powietrze. Wtedy boli, cholernie boli. Wczoraj właśnie miał swój dzień. Zaczęło boleć tak cholernie, że zdążyłem tylko powiedzieć: „Mdleję ...” I jak otworzyłem oczy to miałem wokół siebie gapiących się na mnie domowników. Najwyraźniej nie wiedzieli co mają robić. Ocknąłem się gdy odwiedzająca nas właśnie lekarka wołała mnie po imieniu. Podobno byłem blady jak papier. Niewątpliwie Azrael maczał w tym palce. Dostałem zastrzyk przeciwbólowy i przeciwzapalny. Dziś Azrael wyraźnie odstępuje. Azraela zresztą poznałem już wcześniej, z powieści Akunina, ale tam to nie był kot. Jako kot Azrael jest pomarańczowy, kot domowy krótkowłosy. Obejrzę może dziś na dobranoc film dokumentalny w którym gra ważną rolę:
Bo koty jak ludzie – bywają różne. U mnie koty występowały w paru ostatnich notkach. Najpierw Szaruś, potem Dżafar. Dziś kolej na Azraela, ale z braku scenariusza wezmę ideę od BJABA. W komentarzach pod poprzednią notką Szaruś, Dżafar i kwaternionowy śnieg pytał
A jakby było tam ograniczenie na liczby zespolone w postaci |z|=1 to jakby to pole wyglądało na obrazku R^2?
Wyglądałoby jakoś tak: strzałki równej długości rozłożone na pojedynczym okręgu.
A jakby wyglądał rzut stereograficzny tego pola na prostą?
Strzałki już nie byłyby równej długości.
Więc rzut jakoś tak zniekształca obraz sytuacji.
Najmniejsze zniekształcenie jest w okolicach punktu (0,0).
Stąd moja prośba o rysuneczki z notki ale w pobliżu punktu (0,0,0,0) czyli w pobliżu (0,0,0).
""Czy wszystkie okręgi na rysunkach przechodzą przez (mają punkt wspólny) (0,0,0) ? "
To są trajektorie nieosobliwego pola wektorowego. One się w ogóle nie przecinają."
No ale czy są styczne w (0,0,0)?
Wydaje się, że powierzchnie na rysunkach obejmują jedne drugie. Czy przypatrując się coraz mniejszym powierzchniom dochodzimy do granicy w postaci okręgu czy punktu?
Kolejne pytanie.
Na jaką trójprzestrzeń rzutujesz w rzucie stereograficznym (na styczną do sfery S^3, czy na przechodzącą przez jej środek)?
"Odpowiem dziś."
Już zapowiedź cieszy.
Pytania świetnie trafione na ból zęba. Kot Azrael nie mógłby trafić lepiej. Umarłego poderwałyby do życia. I poderwały!
Najpierw załatwmy sprawę z przykładem z liczbami zespolonymi. W notce W poszukiwaniu czwartego wymiaru pokazałem obrazek w płaszczyźnie liczb zespolonych
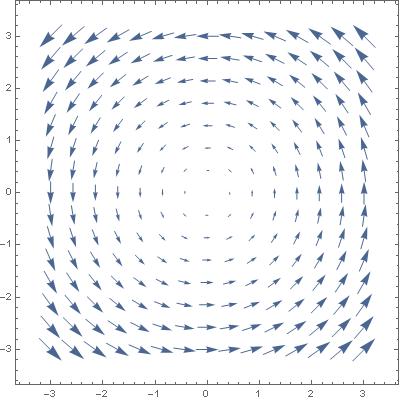
Jest to pole wektorowe powstałe z mnożenia liczb zespolonych przez jednoparametrową grupę liczb zespolonych o module 1
u(t) = exp (it) = cos t + i sin t
Oczywiście powinienem był wziąć to pole wektorowe jedynie na liczbach zespolonych o module 1, bo podobnie robię potem z kwaternionami. Zatem mój obrazek powinien wyglądać tak
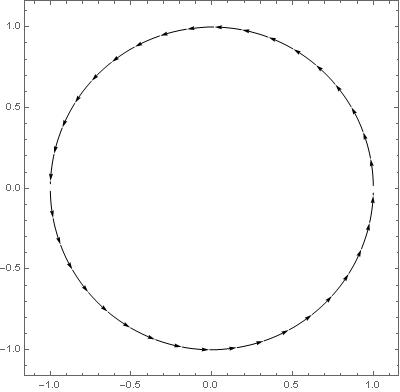
Co jest poza okręgiem o promieniu 1 mnie nie interesuje.
By odpowiedzieć na pozostałe dociekliwe pytania, skoncentrujmy się na jednym polu wektorowym, konkretnie na v3P, tym powstałym z mnożenia z prawej przez exp(tk). Bo na tym właśnie polu bawił się kotek Szaruś w notce Szaruś na zimowych kwaternionowych polach.
V3P = (-Z,Y,-X,W)
Interesuje nas to pole na trójwymiarowej sferze kwaternionów jednostkowych tzn. takich że
X2 +Y2 +Z2 +W2 = 1
Pole jak, pole, ale mamy to pole na razie w czterowymiarowej przestrzeni, styczne tam do trójwymiarowej sfery. Z tej sfery rzutujemy na trójwymiarową przestrzeń rzutem stereograficznym. I ten rzut staje się podstawą wszczęcia śledztwa przez majora BJABA. Dlaczego majora? Otóż poniekąd z powodu kłopotów z zębami zabrałem się za detektyw Aleksandry Marininej „Złowroga pętla”. Główną rolę odgrywa tam analityk śledczy major Anastazja Kamieńska.
Nastja dobra jest. I BJAB jest dobry. Stąd mi się skojarzyło. Podejrzany jest Rzut Stereograficzny. Pociągnijmy za sznurki, przeprowadźmy inwigilację, rozpytajmy sąsiadów.
Od zmiennych W,X,Y,Z na 3-sferze jednostkowej przechodzimy do zmiennych x,y,z w trójwymiarowej przestrzeni. Formuły były w notce Trójwymiarowa sfera - codziennie z nowym uczesaniem. Oto „briefing” stamtąd:
Przejście od W,X,Y,Z w czterech wymiarach do x,y,z w trzech wymiarach jest dane formułami
x = X/(1-W), y = Y/(1-W), z = Z/(1-W).
Biegun z którego rzutujemy to punkt W = 1,X = Y = Z = 0. Przejście odwrotne od x,y,z na sferę jest dane wzorami
W = (r2-1)/(r2+1), X = 2x/(r2+1), Y = 2y/(r2+1), Z = 2z/(r2+1),
gdzie r2 = x2 + y2 + z2.
No, nieźle, jak na początek śledztwa to nieźle. By dostać x=y=z=0, musimy mieć X=Y=Z=0. Wtedy z konieczności (norma =1) musi być W=1, lub W = -1. To pierwsze jest niemożliwe, bowiem wtedy mianownik 1-W by się zerował. Zatem W=-1. Czyli nasza 3-wymiarowa sfera leży na 3-wymiarowej przestrzeni na którą rzutujemy. W ten sposób załatwiamy odpowiedź na pytanie „Na jaką trójprzestrzeń rzutujesz w rzucie stereograficznym (na styczną do sfery S^3, czy na przechodzącą przez jej środek)? „
Teraz trzeba przejść z polem wektorowym w czterech wymiarach do pola wektorowego w trzech wymiarach przez rzut stereograficzny. Ten punkt (na razie) opuszczę, bo tu „biez wodki ne razberiosz”. Major Anastazja wolała raczej Martini. Może być i Martini .
Po Martinim otrzymujemy taki wynik
V3P(x,y,z) =(y-xz, -x-yz, (r2-1)/2)
(Dodane następnego dnia: Ta ostatnia formuła jest błędna, Patrz następna notka. Nie należy pracować po Martini.)
Śledztwo interesuje się otoczeniem punktu x=y=z=0. W punkcie tym nasze pole ma wartość
V3P(0,0,0) = (0,0,-1/2)
Czyli strzałeczka skierowana w dół. Chcemy teraz przeprowadzić wizję lokalną i zobaczyć co znajdziemy w okolicach tego punktu. No to wybieramy do badania mały kawałek płaszczyzny z=0, Na przykład x,y zmieniają się od -1, do 1, zaś z=0.
???????????????????????????????????????????????????
Tu w toku śledztwa wyszły na jaw nowe nieoczekiwane okoliczności. Wersja zamachu, poprzednio raczej wykluczana, teraz musi być wzięta na nowo. Działają jakieś niezidentyfikowane obce siły. Muszę je zidentyfikować, logicznie wyjaśnić.







Komentarze
Pokaż komentarze (6)