Dwa obozy spierają się o wynioski i wynki analizy Biniende. W dyskusji uwaga głównie skupiona jest na jakości odwzorowania konstrukcji lub parametrach materiału. Poniżej wykaże, że metoda obliczeń zastawano prze Biniende ma fundamentalne błędy, które prowadzą do nierzeczywistych wyników, bez względu na to jak dokładnie modelowany jest skrzydło, drzewo lub z jaką dokładnością znane są parametry materiału. Innymi słowy, fundamentalnie metoda jest zła i nie powinna być stosowana do modelowania problemów pękania materiału takiego jak drewno.
Uwagę skupiam na jednym z zagadnieniu, tzn. modelowaniu zniszczenia drzewa za pomocą metody erozji elementów. Wykazanie błędu w tym elemencie algorytmu jest warunkiem wystarczającym do wykazania całościowej niepoprawności wyników. Pomijam inne problemy natury fizycznej i numerycznej, uważam że niepotrzebnie rozproszą uwagę czytelnika. Jednak w przypadku gdyby ukazał się raport lub publikacja naukowa, wszystkie elementy modelu powinny poddane być dalszej szczegółowej krytyce.
W podejściu zastosowanym przez Biniende zastosowano normę dewiatora odkształceń jako kryterium erozji elementu skończonych. Historycznie metoda ta została wprowadzona do LS-DYNA by umożliwić obliczenia w przypadku gdy elementy skończone ulegają dużej dystorsji w wyniku odkształceń plastycznych. Współcześnie zalecane jest stosowanie, jeżeli to tylko możliwe, podejścia opartego na dowolnym opisie Lagranżowsko-Eulerowskim, które eliminuje problem dystorsji elementów skończonych. Ze względu na prostotę podejścia na początku lat 90 zaczętą ją stosować do modelowania zniszczenia, szybko jednak pojawiła się duża liczbę opracowań naukowych prezentujących ułomność takiego podejścia (dla hasła <<"mesh dependency" damage>> google podaje 7280 odwołań).
Pomijam w tym punkcie szereg innych problemów natury numerycznej mogących mieć znaczący wpływ na końcowy wynik, chociażby kompletny brak analizy zbieżności rozwiązania. Nadal otwartym problemem naukowym jest miara wytężenia drewna, przejęcie w obliczeniach normy dewiatora odkształceń jest arbitralne i nie ma dobrego uzasadnienia, poza prostotą.
Skupiając uwagę na zastosowanej przez Biniende metodzie można zauważyć że, po pierwsze metoda erozji elementów nie zachowuje masy, pędu i energii w układzie, łamiąc fundamentalne prawa mechaniki. Po drugie, algorytm wymaga regularyzacji i w senie matematycznym problem jest źle postawiony (istnieje ogromna liczba publikacji na ten temat). W rezultacie ustanowiona granica przy której usuwane są elementy nie może być uznana za parametr fizyczny materiału a jest parametrem modelu, tzn. zależy od własności materiału i warunków brzegowych/początkowych. W szczególnych przypadkach zdarza się, że ten parametr modelu można dobrać w taki sposób by numerycznie odtworzyć eksperyment. Ale nie można go z góry wyznaczyć, zbadać, by przewidzieć jaka będzie odpowiedź eksperymentu. Podsumowując, taki model nie ma zdolności predykcyjnych i powinien być stosowany wyłącznie gdy jest weryfikowany przez eksperyment, który bezpośrednio jest modelowany. Mimo tych ograniczeń, metoda stanowi potężne narzędzie w rękach inżyniera, wymaga jedynie świadomego użytkownika.
Argumentacja Biniendy opiera się na podstawowym złożeniu, że jego model jest fizyczny. Taka argumentacja i późniejsze wnioski oparte są niesłusznym założeniu o fizyczności modelu opartego na uniwersalnych prawach fizyki, gdy w rzeczywistości model ten prawa fizyki narusza. Bininda podkreślając zalety swojego modelu odwołuje się do matematyki, gdy w rzeczywistości w sensie matematycznym jego problem jest źle postawiony [Rice, 1976 (ponda 1000 cytowań), De Borst (199?) ].
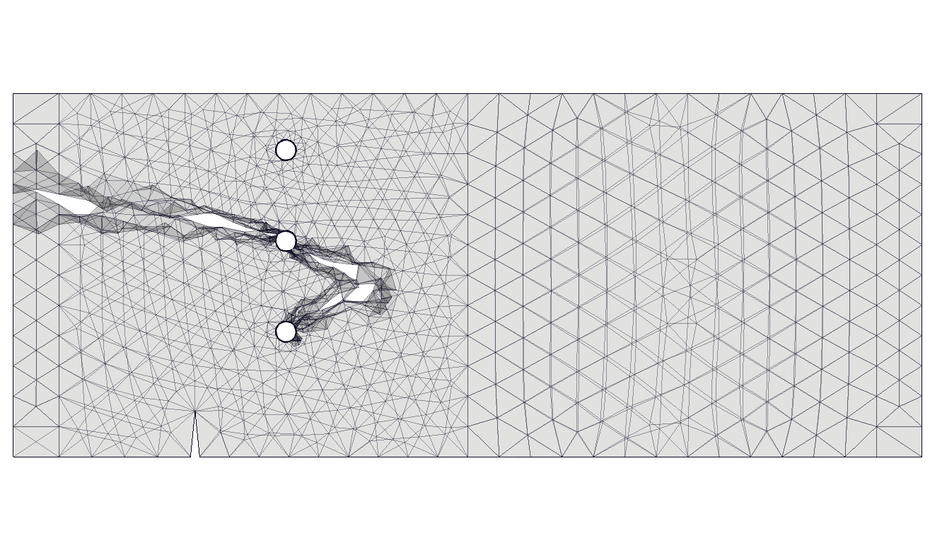
Poniżej przedstawiam przykład do jakich niezgodności modelu z doświadczeniem prowadzi metoda erozji elementów. Do testu numerycznego został wybrany klasyczny eksperyment z 3 otworami. Parametry materiału i gematrie zostały przyjęte jak w artykule [http://dx.doi.org/10.1016/0013-7944(95)00247-2]. Z uwagi na to, że skupiamy się tutaj na metodologii, rozważany materiał nie ma tutaj znaczenia.
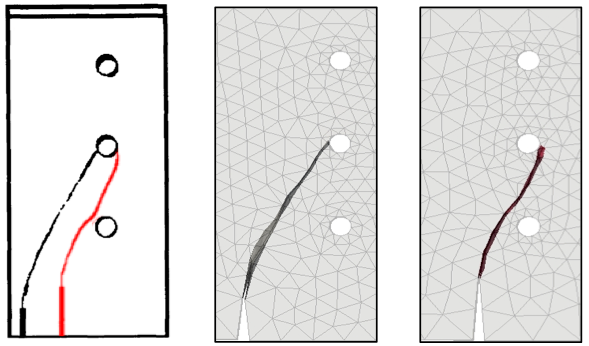
W analizie użyto czworościenne elementy wyższych rzędów z hierarchiczną aproksymacją przemieszczeń. Obliczenia referencyjne, z właściwą ścieżką rysy zostały wykonane za pomocą metody prezentowanej w artykule [http://dx.doi.org/10.1016/j.cma.2008.12.028].
Należy podkreślić, że miara wytężenia materiału oparta na dewiatorze odkształceń nie jest właściwą dla eksperymentu z [http://dx.doi.org/10.1016/0013-7944(95)00247-2]. Stosowana jest tutaj ponieważ jest prostym przeniesieniem miary zastosowanej przez Biniende. W tym przypadku, ponieważ jest to izotropowa miara wytężenia dla izotropowego materiału, w przypadku modelu z Arkon jest ona naiwnie stosowana w przypadku ortotropowego materiału jak drewno.
Weryfikując wyniki otrzymane metodą z Akron, zauważymy nierealistyczną propagację rysy, zobacz rys. 1, całkowicie niezgodną z eksperymentem. Mimo inicjacji rysy, pękanie propaguje się ze środkowego otworu a końcowy wynik jest niezgodny z rzeczywistym. Otrzymane wyniki sprawiają jednak iluzie, że są poprawne.
Wyniki mogły by ulec lekkiej poprawie w przypadku mocnego zagęszczenia siatki, ale niepożądana zależność ścieżki od siatki pozostanie. Innymi słowy, takie podejście w ogólnym przypadku nie umożliwia obiektywnego odtworzenia eksperymentu lub predykcji zachowania konstrukcji. W przypadku skomplikowanych konstrukcji obciążonych dynamicznie niezgodności modelu z rzeczywistością na ogół są jeszcze większe.
Dla kompletności wywodu, na rys. 2 i 3 przedstawiam poprawne wyniki symulacji numerycznej z wykorzystaniem współczesnych metod. Każda metoda numeryczna wymaga analizy zbieżności, rys. 4 przedstawia zmianę energii sprężystej dla różnych gęstości siatki. Proszę zauważyć, że wraz z zagęszczaniem siatki wyniki nie ulegają istotnej zmianie, tzn. rozwiązanie się zbiega. Dodam, że dla metody erozji elementówm rozwiązanie się nigdy nie zbiegnie, nawet dla nierealistycznie gęstych siatek.
Podsumowując, metoda erozji elementów dla materiał izotropowego dla klasycznego eksperymentu tarczy z trzema otworami daje niepoprawne wyniki. W bardziej złożonych przypadkach (dynamiczne obciążenie i anizotropowy materiał jak drewno) jest naiwnie zakładać, że metoda zastawana przez zespół z Arkon da poprawne wyniki.
Powyższa argumentacja jest tylko wstępem do pełnej krytyki, jest otwartym pytaniami czy szczegółową krytyka ma sens dopóki podstawowe błędy nie zostaną wyjaśnione przez zespól Biniendy, w co wątpię.










Komentarze
Pokaż komentarze (190)