Geometria kształtów

Kontynuując naszą serię o fraktalach zatrzymamy się na chwilę na ważnym temacie: geometrii kształtów. Bowiem to co bodaj najważniejsze w naszym widzeniu w ogólności, a we fraktalach w szczególności – to kształty, ich podobieństwo, a także ich niezwykłość. Kształty mogą być płaskie, mogą też być przestrzenne – choć jedno oko widzi przestrzeń dwuwymiarowo. Chciałoby się mieć jednak przestrzeń w której kształty są punktami. Tak by, na przykład, można było tam narysować „geodezyjną” - najkrótszą linię łączącą jeden kształt z innym kształtem („morfing”). Chciałoby się podeprzeć praktykę informatyków jakąś poważną matematyką – bo matematyka może wnieść coś nowego i istotnego do praktyki – tak bywa.

Geometria (a także analiza statystyczna) kształtów to dziś obszerna i mocno zaawansowana dziedzina. Zainteresowałem się nią trochę ze względu na fraktale. Punktem startowym jest tu „odległość Hausdorffa”. I choć praktycy od kształtów traktują to pojęcie jako zbyt teoretyczne i (bez przeróbek) w praktyce mało przydatne, niemniej jest to pojęcie ważne i ciężko bez niego zrozumieć istotę konstrukcji fraktali typu zbiór Cantora, trójkąt Sierpińskiego, kostka Mengera i podobnych.

Omawiając odległość (metrykę) Hausdorffa oswoimy się przy okazji z ideą, że zbiory w przestrzeni same mogą być punktami innej przestrzeni: przestrzeni zbiorów. Jednak, jak to zwykle bywa, diabeł ukrywa się w detalach, a diabłu (diablicy?) na imię Matematyka.

Devil Mathematics

By nie komplikować sprawy ograniczmy się do tworów płaskich – na dwuwymiarowej płaszczyźnie wyposażonej w geometrię Euklidesowa, gdzie odległość pomiędzy punktami dana jest wzorem znanym co najmniej od czasów Pitagorasa. Interesować nas będą zbiory punktów tej płaszczyzny, ale nie wszystkie zbiory: jedynie zbiory zwarte. „Zwarty” oznacza w tym przypadku „ograniczony i domknięty”. Co to jest zbiór ograniczony tłumaczyć chyba nie trzeba – to zbiór który daje się cały zawrzeć w kole o skończonym promieniu. Nieco subtelniejsza sprawa jest z pojęciem „domkniętości”. Intuicyjnie: zbiór jest domknięty gdy zawiera swój brzeg. Weźmy na przykład dysk jednostkowy: to jest zbiór („miejsce geometryczne”) tych wszystkich punktów, których współrzędne (x,y) spełniają nierówność

x² + y² ≤ 1.

Jest to zbiór zwarty. Zamieńmy nierówność nieostrą „≤ „na ostrą „<” i od razu zbiór przestaje być zwartym (bo przestaje być domkniętym. Jego brzeg – okrąg jednostkowy w samym zbiorze się bowiem nie zawiera.

Albo usuńmy jeden choćby punkt, na przykład środek (0,0), i już zbiór przestaje być domknięty – bowiem punkt ten należy wtedy do brzegu („przywiera” do zbioru), a z samego zbioru go wyrzuciliśmy.

Rozważmy teraz (wciąż na płaszczyźnie) zbiór wszystkich niepustych zbiorów zwartych. Czy coś takiego w ogóle istnieje? Standardowa teoria mnogości zapewnia nas, że coś takiego istnieje, choć z przeliczeniem jest trochę trudno.

Oznaczmy zatem zbiór wszystkich zwartych i niepustych podzbiorów płaszczyzny symbolem H(E²). „E” bo euklidesowa, „2” bo dwuwymiarowa, „H” boFelix Hausdorff (nazwisko niemieckiego matematyka).

Z Wikipedii:

Felix Hausdorff (ur.8 listopada 1868 roku weWrocławiu (wówczas Breslau), zm.26 stycznia 1942 roku Felix Haudorff

wBonn) –niemiecki matematyk, jeden z twórcówtopologii.

....

W roku1941 Hausdorff wraz z rodziną znalazł się na liście osób przeznaczonych do wywiezienia do obozu koncentracyjnego, lecz dzięki interwencji Uniwersytetu w Bonn zdołał tego uniknąć. Nie mogąc znieść życia w stanie permanentnego zagrożenia 26 stycznia 1942 roku Hausdorff wraz z żoną popełnili samobójstwo.

To nasza przestrzeń. W tej przestrzeni określa się odległość między punktami (zatem: odległość pomiędzy dwoma zwartymi podzbiorami płaszczyzny). Oznaczana jest ona zwykle literką h. Zatem h(A,B) to odległość Hausdorffa pomiędzy zbiorami A i B – dwoma punktami przestrzeni H(E²).

Definiuje się ją na parę równoważnych sposobów. Dla nas bodaj najbardziej zrozumiałą będzie definicja poprzez „delta-otoczenia”. Mając zbiór A wokół każdego punktu tego zbioru malujemy dysk o promieniu delta. To co te dyski pokryją to „delta-otoczenie zbioru A. Mając dwa zbiory zwarte A i B, szukamy najmniejszego delta takiego, że A zawiera się w delta-otoczeniu zbioru B, oraz B zawiera się w delta-otoczeniu zbioru A. Takie najmniejsze delta zawsze istnieje – i to jest właśnie odległość Hausdorffa h(A,B) pomiędzy A i B. Zobaczmy to na obrazku:

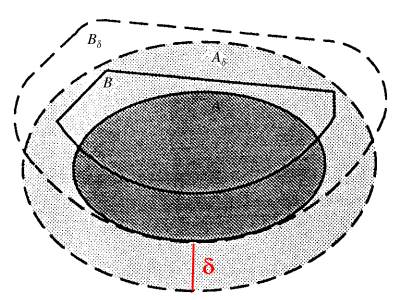
Odległość Haudorffa

(K. Falconer, "Fractal Geometry: Mathematical Foundations and Applications", Wiley 2006)

Zbiór A to ciemna (wypełniona) elipsa. Jej delta-otoczenie zaznaczone jest linią przerywaną. Brzeg zbioru B składa się z czterech segmentów. Jego delta-otoczenie zaznaczone jest inną linią przerywaną. Widać, że A zawiera się w delta-otoczeniu zbioru B i B zawiera się w delta-otoczeniu zbioru A. Są to optymalne delta-otoczenia – zmniejszyć ich już się nie da. Delta-otoczenie elipsy dałoby się trochę zmniejszyć i wciąż zawierałoby B, ale wtedy jednocześnie musielibyśmy zmniejszyć delta-otoczenie zbioru B (ma być to samo delta) – i wtedy kawałek elipsy już by nam poza nie wyskoczył.

Funkcja h(A,B) ma wszystkie potrzebne własności odległości: jest symetryczna, spełnia nierówność trójkąta (trzeba się trochę napracować by to udowodnić), no i jest równa zeru wtedy i tylko wtedy gdy zbiory A i B są identyczne. W pewnym sensie mówi nam o tym na ile dwa zbiory (kształty) są sobie bliskie. W zastosowaniach do grafiki komputerowej i do rozpoznawania obrazów nie bardzo się przydaje, bo wystarczy dodać do jednego ze zbiorów jeden tylko „zabłądzony” punkt i już odległości istotnie się zmieniają. Chyba, że ograniczymy klasę zbiorów, które nas interesują i ograniczymy się do zbiorów „regularnych” w jakimś tam sensie (na przykład do takich, których brzeg jest „regularną”, „wystarczająco porządną” krzywą. Tak się też zwykle robi.

Temat ten będziemy kontynuować w następnej notce. Tutaj jedynie pokaże dwa obrazki zaczerpnięte z monografii ”Statistics and analysis of shapes”, Hamid_Krim, Anthony Yezzi, Birkhauser 2006. Pierwszy pokazuje „najkrótszą linię łączącą dwa kształty” (pięć przykładów). Oczywiście „najkrótsza” oznacza w praktyce „najkrótsza w ramach dostępnej biblioteki kształtów”.

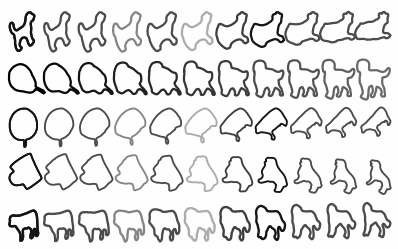
Drugi to „kształt średni”, gdzie „uśrednia się” osiem rybich kształtów.

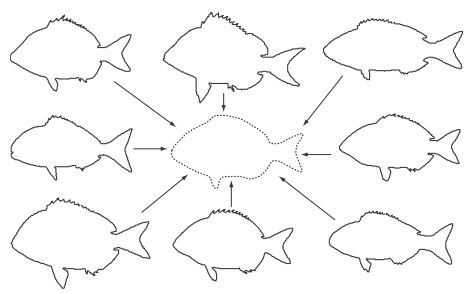
Takimi i podobnymi (ale poważniejszymi) sprawami zajmują się spece od kształtów. A zadanie mają trudne. Komputer świetnie odczytuje kody paskowe w supermarkecie, ale z kształtami, choćby z rozpoznawaniem odręcznego pisma – wciąż jest słabo!