Cały czas wychodzą drobne niedociągnięcia, wciąż trzeba korygować i poprawiać ale droga do doskonałości to wyszukiwanie błędów i nieustanna ich korekta, a doskonałość to i tak utopia do której należy dążyć ze świadomością że nigdy się jej nie osiągnie.
Mam poprawne wyniki ale nieustanny problem ze znakiem, coś źle liczę albo coś źle interpretuje.
Bazą pod wzory Eulera jest
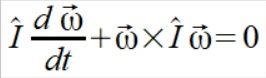 (1)
(1)
Ponieważ

i
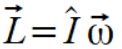
to teraz mamy inny zapis wzoru (1)
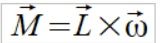 (1a)
(1a)
Podręczniki każą tu interpretować prędkość kątową jako prędkość kątową nieinercjalnego układu odniesienia, tylko że ten wzór również opisuje obroty ciała sztywnego w inercjalnym układzie odniesienia, a Euler wstawił tu inercjalną prędkość kątową bryły sztywnej.
Jeżeli do tego wzoru wstawimy nieinercjalną ωni układu odniesienia, to wzór wskaże nam pozorny moment siły wynikające z transformacji układu odniesienia z inercjalnego do nieinercjalnego.
Jeżeli wstawimy do wzoru inercjalną prędkość kątową ciała sztywnego, to wzór wskaże nam jak najbardziej inercjalny moment siły ciała sztywnego.
Już dawno zauważyłem że wzory te w niektórych sytuacjach można z powodzeniem stosować również dla jednego punktu a równania Eulera są wynikiem sumy wyników dla wszystkich punktów. Jeżeli ktoś powie że moje przypuszczenia nie są udowodnione i nie wiadomo czy te założenie jest prawdziwe to ma racje, trzeba to jeszcze udowodnić. Ja jednak działam nieszablonowo dlatego widzę więcej niż inni a moje metody bronią wyniki.
Mamy więc takie punkty ciała sztywnego

policzymy tylko punkt m1. Wzór na wektor prędkości punktu
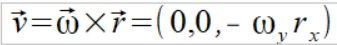
Wzór na przyspieszenie "dośrodkowe" (lepszym terminem jest doosiowe)
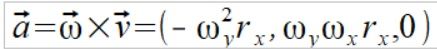
Wektor przyspieszenia razy masa to wektor siły który nie jest równoległy z wektorem położenia punktu, oznacza to że daje on moment siły
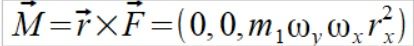 (2)
(2)
Teraz sprawdzenie tego wyniku czy jest spójny ze wzorem (1a). Moment pędu punktu to
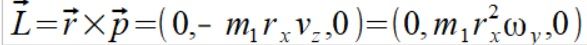
Wstawiamy wzór (1)
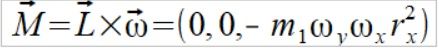 (3)
(3)
czyli wynik nie jest dokładnie taki sam jak oczekiwałem, moment siły wyliczony z siły więzów (2) ma tą samą wartość co moment siły wyliczony ze wzorów Eulera (3) ale przeciwny kierunek. Nie wiem czy gdzieś robię błąd czy też coś źle interpretuje.
Te momenty sił nie są sprzeczne z żadnym prawem Fizyki i bazują na wzorach książkowych. Fizycy nie są świadomi ich istnienia a można łatwo pokazać czym one są, trzeba tylko schować emocje i umieć obiektywnie czytać wzory

Aby go poprawnie stosować trzeba go uzupełnić
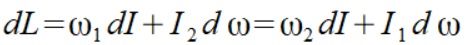
Gdzie indeksem 1 jest stan początkowy indeksem 2 stan końcowy
mamy tutaj dwa przeciwne momenty sił, jeden odpowiada za zmianę prędkości kątowej drugi skutkuje zmianą momentu bezwładności

Podczas obrotu ciała sztywnego zmienia się chwilowa prędkość kątowa ale również chwilowy moment bezwładności, jak widać przyroda sama znalazła mechanizm aby zrównoważyć powstający moment siły i równanie znalazło rozwiązanie aby się wyzerować. Z tego co przypuszczam (nie rozgryzłem tego jeszcze) moment siły wywołany zmianą momentu bezwładności jest tworem matematycznym nie oparty na żadnej sile. Fizycy którzy stworzyli teorie kwantów nie powinni mieć problemu ze zrozumieniem tego.








Komentarze
Pokaż komentarze (1)