Miałem zapisać szkic roboczy a niechcący opublikowałem:) Po trochę będę aktualizował ale pewnie zajmie to parę dni, może ktoś się dołączy.
Był mały błąd przy liczeniu a3k współrzędna x powinna być 3/40 a było 2/20. Po korekcie suma sił wyszła zero a moment siły jest przeciwny do spodziewanego ale z tą samą wartością. Teraz muszę się zastanowić dlaczego tak wyszło.
Pozostaje już to policzenia ostatni przykład o który kiedyś pytałem, jak działają siły więzów na punkty ciał sztywnych podczas ich obrotu?
Ostatni przykład wydał mi się obecnie zbyt prosty dlatego trochę w nim namieszałem aby sprawdzić czy w bardziej skomplikowanych BS siły więzów również się zerują.
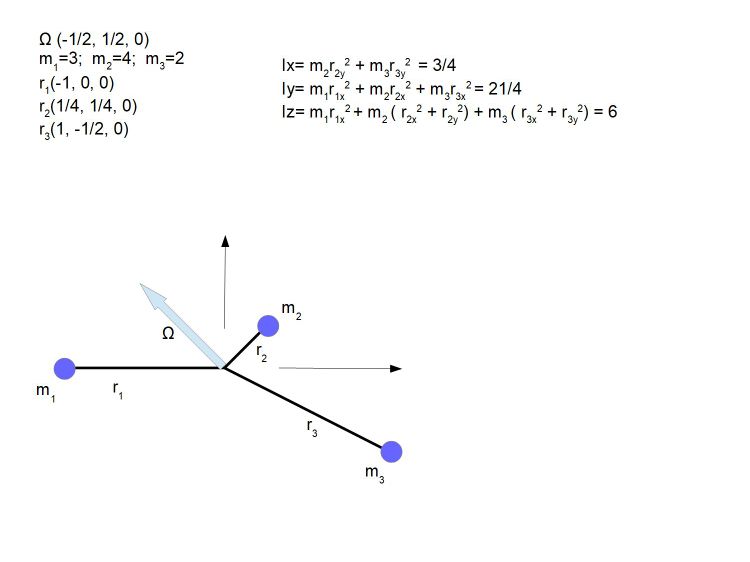
Poprzedni przykład był fajny do liczenia, było tam sporo symetrii powtarzających się wartości i jedyne. Fajnie wszystko się uprościło ale może był szczęśliwy traf i przy innych BS wynik będzie inny. Trzeba to sprawdzić, teraz unikałem wartości 1 kątów prostych czy jakiejkolwiek symetrii.
Co musimy osiągnąć aby nie naruszyć obecnie uznanych praw Fizyki?
Z prawa zachowania pędu, wszystkie wektory sił więzów po zsumowaniu muszą się zerować
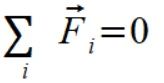
Wynik musi być zgodny z równaniami Eulera dla ruchu obrotowego bryły sztywnej które są zgodne z prawem zachowania momentu pędu.
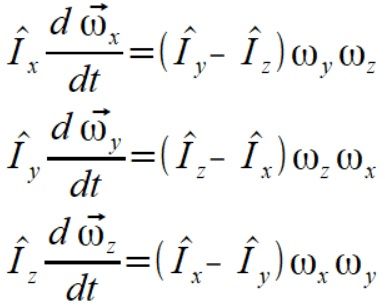
Pamiętamy że tensor bezwładności razy wektor przyspieszenia kątowego to wektor momentu siły
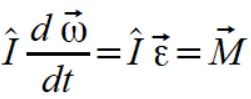
Nasza prędkość kątowa ma jedynie dwie współrzędne x i y więc jedynie trzecie równanie Eulera jest niezerowe
Mz=9/8
Taki też musimy uzyskać moment siły na osi z.
Zaczynamy od wyliczenia wektorów prędkości dla punktów
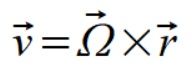
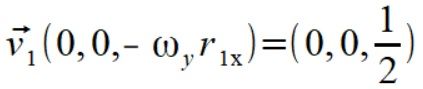
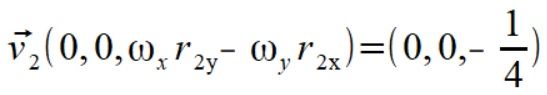
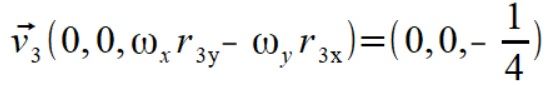
Liczymy teraz składowe prostopadłe prędkości kątowych dla punktów
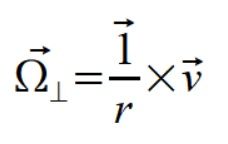
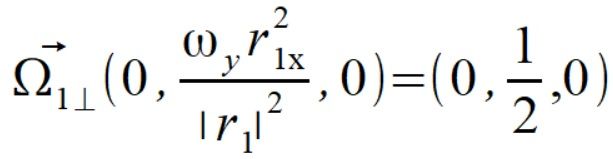
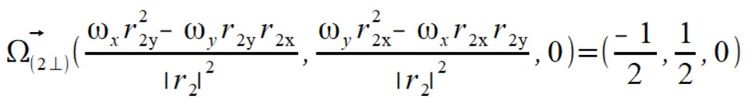
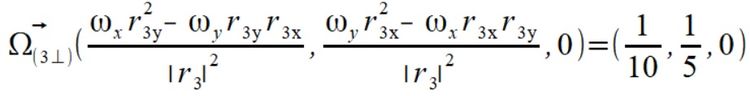
Liczymy teraz składowe równoległe prędkości kątowej dla punktów
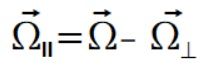
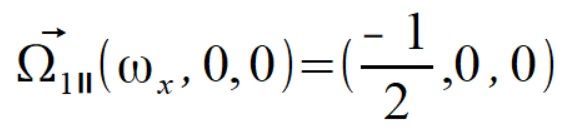
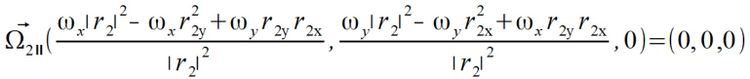
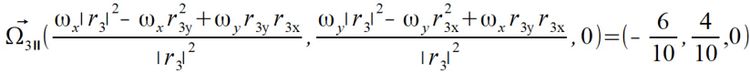
Można sobie sprawdzić że sumując składową prostopadłą i równoległą prędkości kontowej dla każdego punktu uzyskujemy wektor 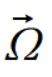 . Dalsze liczenie na zmiennych nie ma więc większego sensu bo skoro wektory prędkości kontowej się zgadzają to i przyspieszenia za jej pomocą będą poprawne, dlatego przechodzę do liczenia na liczbach.
. Dalsze liczenie na zmiennych nie ma więc większego sensu bo skoro wektory prędkości kontowej się zgadzają to i przyspieszenia za jej pomocą będą poprawne, dlatego przechodzę do liczenia na liczbach.
Teraz liczymy przyspieszenia punktów ze wzoru
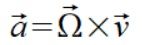
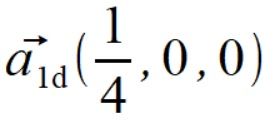
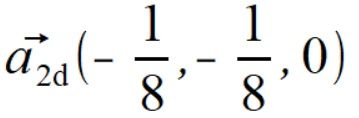
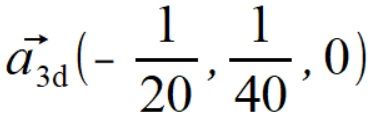
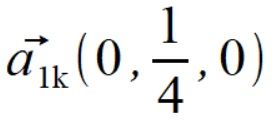
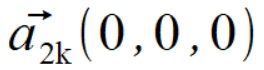 .
. 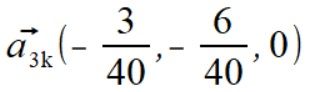 .
.
Wyznaczamy siły działające na punkt
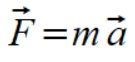
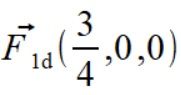
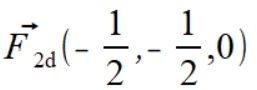
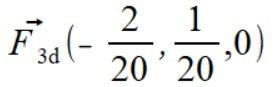
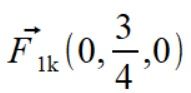
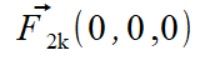 .
.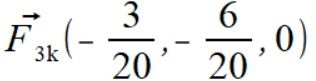 .
.
Fd to siły dośrodkowe równoległe do wektora położenia nie dające momentu siły. Wyliczamy więc moment siły z Fk
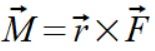
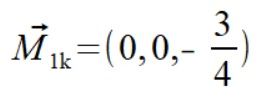 .
.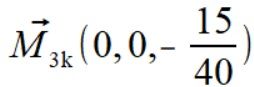 .
.
Nasz moment siły wyszedł Mz=-1,15 a spodziewałem się 1,125. Nie jestem zaskoczony bo rzadko kiedy jestem w stanie tyle policzyć po nocach by nie popełnić błędu. Wynik powinien być albo taki sam albo całkowicie inny, znak minusa może być wynikiem błędu w którymś z licznych kalkulacjach iloczynu wektorowego pozostała różnica to 1/40 i tez może być różnicą wynikającą z błędu w obliczeniach. Suma sił też daje niewielką wartość
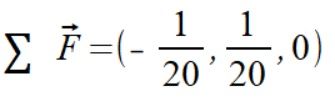
Wygląda mi to na mały błąd gdzieś w liczeniu punktu trzeciego ale teraz trzeba to sprawdzić. Teraz muszę znaleźć ten błąd albo zastanowić się czemu wartości nie są takie jakie bym się spodziewał. Ale to już nie na dzisiaj.
Intuicja mnie nie myliła, niewielkie różnice między tym co oczekiwałem a tym co i wyszło za pierwszym razem były wynikiem jednego małego błędu przy ak3. Jest jeszcze jeden problem gdzie nie mogę znaleźć błędu bo oczekiwałem moment siły 9/8 a uzyskałem -9/8. Suma wektorów sił wynosi zero zgodnie z oczekiwaniem.
Zadziwiające że cały ten skomplikowany rachunek i wiele zmiennych tak ładnie się zgrały. Jest to druga BS druga pozytywna weryfikacja mojej metody. Jak teraz udowodnić że metoda ta zawsze jest prawdziwa?
Inne tematy w dziale Technologie

