Wydawało się że czasy dogmatów i przynależności klanowej przeminęły wraz ze średniowieczem i pojawieniem się renesansu. Wydawało by się że obecnie rządzi rozum i poszukiwanie prawdy. Wydawało by się że współcześnie nie ważne kim jesteś, gdzie się urodziłeś, bo jeżeli masz talent i poprawne wyniki to masz szanse się wybić. Tak wygląda propaganda obecnych czasów, chyba nigdy tak nie było, na pewno teraz tak nie jest i pytanie jest czy kiedyś uda się to zmienić i pokonać nasze ludzkie słabości i własne ego.
Od kilku już lat szukając odpowiedzi na temat zagadnienia obrotu punktu w ciele sztywnej, wszystkie wyjaśnienia jakie czytałem wydawały mi się nie pełne i czasami w sobie sprzeczne. Przez długi czas nie umiałem tego zdefiniować i udowodnić ale nadszedł czas kiedy mogę to już zrobić. Przykładem takiego błędu jest twierdzenie że siły więzów muszą być siłami centralnymi, bo inaczej rzekomo musiały by łamać fundamentalne prawa Fizyki. Jest to tylko książkowe założenie, które nie dało się udowodnić, a teraz jak wynika z moich obliczeń jest fałszywe, co z resztą z łatwością można udowodnić i każdy kto ma jakie takie pojęcie czym jest iloczyn wektorowy może to zrozumieć.
W podręcznikach z łatwością znajdujemy wzór na przyspieszenie dośrodkowe
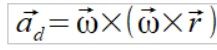
Iloczyn wektorowy wektora omegi na wektor położenia to oczywiście wektor prędkości punku v. Dlatego tez można to zapisać w prostszej postaci
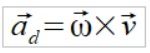
ale tego prostszego wzoru nie znajdziecie w żadnym podręczniku. Własnością iloczynu wektorowego jest to że wektor będący jego wynikiem jest zawsze prostopadły do wektorów go tworzących i każdy Fizyk o tym wie. Siły centralne są siłami skierowanymi zawsze do jakiegoś jednego centralnego punktu. A siły więzów F=mad zawsze będą prostopadłe do wektora prędkości kątowej.
Przykład dla układu płaskiego który jest łatwiejszy do zrozumienia. Siły więzów albo będą leżeć na tej samej prostej albo będą do siebie równoległe czyli nigdy przenigdy się nie przetną, nie ma takiej możliwości by kierunki tych sił przecinały się w jakimkolwiek punkcie. Definitywnie siły więzów nie są siłami centralnymi.
Przykład
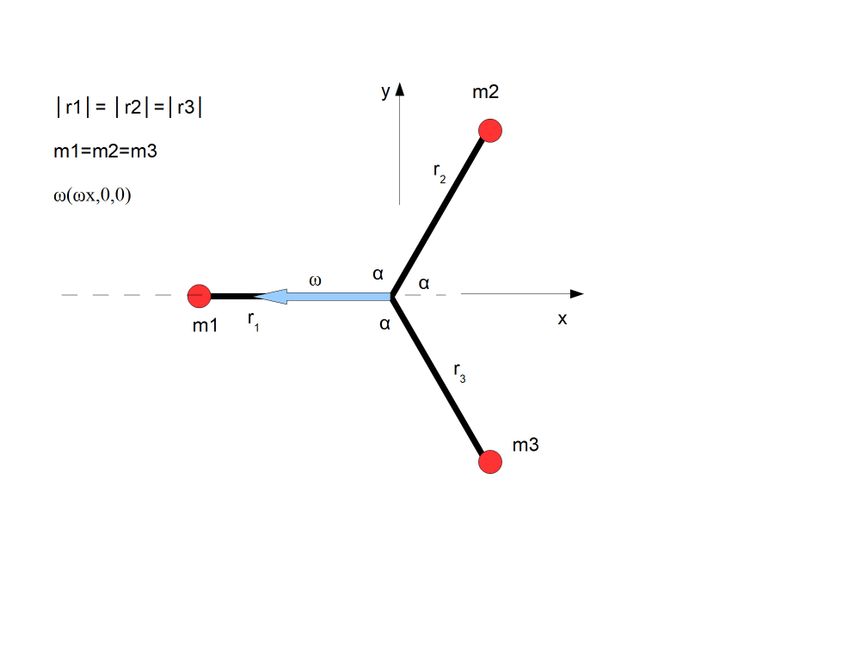
Punkt m1 znajduje się na osi obrotu, punkty takie nie posiadają prędkości liniowej, czyli nie ulegają przyspieszeniom czyli nie działają na nie żadne siły. Jeżeli siła była by centralna skierowana do środka ciężkości to ich suma nie była by zero i taki układ łamał by prawo zachowania momentu pędu.
Inny przykład
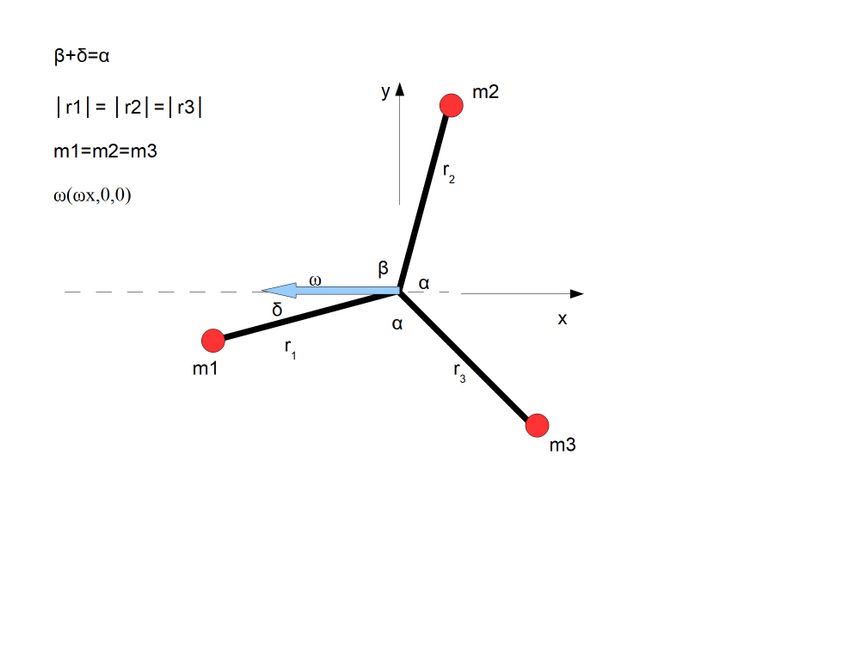
Liczymy siłę więzów dla punktu m2
W(wx, 0, 0); r (rx, ry, 0)
Wektor prędkości punktu
V = W x r = (0, 0, wx ry)
siła działająca na punkt
F= m (W x V) = m(0, wx2 ry, 0)
Jak widać siły więzów zawsze będą prostopadłe do osi obrotu i w układach płaskich zawsze będą do siebie równoległe czyli nie mogą się przecinać w żadnym punkcie.
Nie ma tu skomplikowanej matematyki i to już dawno dawno temu powinno być wypatrzone i poprawione. Dlaczego nie jest? Bo żaden Fizyk nie tego nie uzna i spłynie to po nim jak po kaczce, bo prawda się nie liczy, liczy się przynależność klanowa. Nikt nie będzie nam mówił że białe jest białe a czarne jest czarne, Fizycy wiedzą lepiej. Nie ma miejsca na argumenty, dyskusje czy porozumienie. Nie istnieje siła która przekonała by Fizyka że siła więzów nie jest siłą centralną a w podręcznikach jest błąd, tak samo jak nie da się przekonać żarliwego katolika by przeszedł na buddyzm, bo to nie jest kwestia rozumu a kwestia wiary.
Wiele komentarzy pod moimi tekstami miała na celu mnie zniechęcić do znalezienia prawdy, nie brakowało tez słów obraźliwych, wyzywania mnie od nieuków, leniów, awanturników i obalaczy. Jednak okazało się mimo że po drodze zrobiłem mnóstwo błędów to jednak w efekcie końcowym doszedłem prawdy i miałem po prostu racje, że nie wszystko w obecnej wiedzy o tym temacie jest prawdziwe. Przyzwoitość nakazywała by gdy udowodni się pomyłkę do pomyłki się przyznać, ale we współczesnym świecie przyzwoitość jest wadą frajerów. Fizyk prędzej wskoczy w ogień aniżeli przyzna że amator miał racje.
„Nie jest grzechem się pomylić,
uparcie trwać w błędzie jest grzechem największym”
Inne tematy w dziale Technologie

