Aby lepiej zrozumieć, jak w przyrodzie funkcjonuje prawo znikomego działania, można posłużyć się komputerowym programem modelującym BlowStand1.exe. W zbiorczym pliku BlowStand1exe.zip znajduje się wymieniony program wykonawczy oraz pliki robocze w formacie blo1. Aby przedstawić funkcjonowanie prawa ZD, będą tu wykorzystane parametry - współrzędne w układzie 0xyz oraz prędkości - dwóch oddziałujących ze sobą centralnie symetrycznych pól - cząstek. Te parametry cząstek są zapisane w roboczych plikach: Episod1a, Episod1b, Episod1c, Episod1d oraz w plikach pochodnych, które powstały po zapisaniu w nich parametrów po pewnym czasie oddziaływania ze sobą tych dwóch cząstek. Oddziaływanie cząstek trwało około 20000 iteracji obliczeniowych, po tym okresie parametry zapisano w plikach Episod1a_19996, Episod1b_19996, Episod1c_19999, Episod1d_20000. Wartości tych parametrów są przedstawione na poniższym wykazie.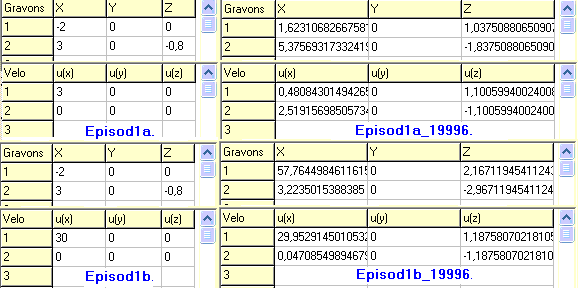
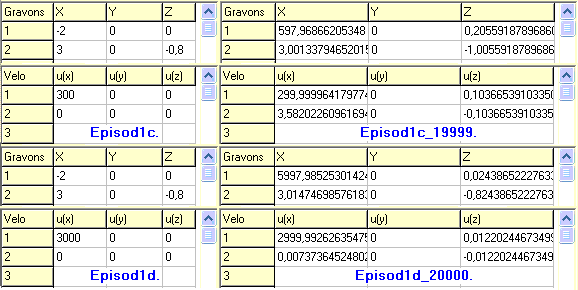
W każdym z przedstawionych czterech epizodów cząstki miały te same początkowe położenia względem siebie. Jedna z nich - cząstka nr 2 - była na początku nieruchoma, a cząstka nr 1 miała pewną początkową prędkość. Kierunek prędkości był taki, aby dochodziło do zderzenia cząstek ze sobą za pośrednictwem ich potencjalnych powłok o promieniu 1,4 jednostek długości. Prędkość początkowa cząstki 1 w każdym epizodzie była inna - były to następujące wartości prędkości: 3, 30, 300 i 3000 jednostek prędkości.
Wzajemne oddziaływanie ze sobą cząstek w programie wykonawczym BlowStand1.exe odbywa się na zasadzie wzajemnego przyśpieszania, podobnie jak to dzieje się w naturze. Obie cząstki mają takie same parametry własne, czyli każda z nich przyśpiesza swoją sąsiadkę według tej samej matematycznej funkcji, która zawiera składową grawitacyjną oraz składową strukturalną. Składowa grawitacyjna ma szczególne znaczenie podczas oddziaływania ze sobą cząstek przy większych odległościach. Natomiast składowa strukturalna zasadniczą rolę odgrywa przy małych odległościach między centralnymi punktami cząstek. Przy tych odległościach cząstki mogą ze sobą tworzyć trwałe wiązania strukturalne - dzieje się tak wówczas, gdy cząstki znajdą się w obszarze powłoki swojej sąsiadki i ich względna prędkość zostanie wyhamowana - albo mogą oddziaływać ze sobą tworząc wrażenie zderzenia i sprężystego odbicia się jednej cząstki od drugiej.
Wzajemne przekazywanie sobie przez cząstki energii kinetycznej odbywa się zgodnie z prawami dynamiki Newtona, a więc, także zgodnie z zasadą zachowania energii. Suma energii cząstek przed zderzeniem jest w każdym epizodzie równa sumie energii, jaką mają cząstki po zderzeniu. Korzystając z tego, że cząstki są jednakowe, zgodność z zasadą zachowania energii można sprawdzić porównując sumę kwadratów prędkości cząstek, jakie mają one (w różnych kierunkach) po zderzeniu i przed zderzeniem.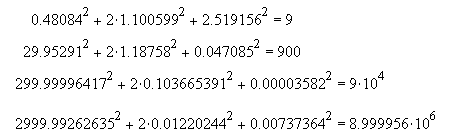
Istnienie pewnej nieścisłości w przypadku epizodu, w którym cząstka 1 miała początkową prędkość równą 3000 j.pr. wynika stąd, jak można przypuszczać, że program wykonawczy prowadził obliczenia przy dt=0,0001, czyli obliczał z pewnym przybliżeniem. Przy małej początkowej prędkości cząstki 1 błąd był niedostrzegalny, ale przy dużej prędkości błąd obliczeniowy stał się widoczny.
Istnienie prawa znikomego działania, które polega na tym, że wraz ze wzrostem względnej prędkości cząstek wzajemne oddziaływanie cząstek staje się coraz mniejsze. Można to dostrzec, gdy porówna się ze sobą odległości pokonywane przez cząstkę 2 oraz uzyskane przez nią prędkości w układzie 0xyz. Obserwując zachowanie cząstek przy ich wzajemnym oddziaływaniu w kolejnych epizodach, można dostrzec, że intensywność reagowania cząstki 2 na obecność cząstki 1 jest mniejsza, gdy początkowa prędkość cząstki 1 jest większa, tak jak to widać poniżej.
Tę zmniejszającą się intensywność oddziaływania widać wyraźnie na podstawie porównania ze sobą wartości energii, jaką w końcowym efekcie posiada cząstka 2, czyli na podstawie porównania kwadratów prędkości cząstki 2. Tak więc, wielkość przekazanej energii w kolejnych przedstawionych epizodach wygląda następująco:
Ta relacja dotycząca przekazywania energii, wynikająca z istnienia w przyrodzie prawa znikomego działania, oznacza, z jednej strony, że przy ogromnych prędkościach cząstek - ale także gdy istnieją one w postaci złożonych materialnych struktur - maleje ich niszcząca działalność na inne złożone struktury. Patrząc na to z drugiej strony, ta zmniejszająca się ilość przekazywanej energii, jak to przedstawiono powyżej, oznacza, że jedynie o taką wartość maleje energia cząstek, które pędzą z dużą prędkością. U tych cząstek należy postrzegać tę energię jako ubytek, który został spowodowany w wyniku oddziaływania na te cząstki "niemal nieruchomej" materii. W tym przypadku oddziaływanie na pędzące cząstki zadziałało hamująco. Ale istnieją urządzenia - akceleratory - które działają na pędzące cząstki przyśpieszająco. W sumie zmienia się jedynie kierunek oddziaływania na szybko pędzące cząstki - zamiast hamowania jest przyśpieszanie - ale prawo przyrody pozostaje to samo. Aby przy coraz większych prędkościach rozpędzanych cząstek można było uzyskać porównywalne przyrosty ich prędkości albo przyrosty ich energii, należy włożyć nieporównywalnie więcej energii. Obecnie dla takiej sytuacji istnieje błędne wyjaśnienie, w którym mówi się, że podczas rozpędzania cząstek do coraz większych prędkości dochodzi do wzrostu ich masy.
Jak z wynika z powyższego, nie ma tam żadnego wzrostu masy pędzących cząstek - istnieje tam jedynie przejawianie się prawa znikomego działania.
Gdy ktoś wnikliwy przeczyta w poprzednim akapicie zdanie: "Aby przy coraz większych prędkościach rozpędzanych cząstek można było uzyskać porównywalne przyrosty ich prędkości albo przyrosty ich energii, należy włożyć nieporównywalnie więcej energii", to może dopatrzeć się pewnego rodzaju sprzeczności, która będzie związana z pojęciem "porównywalności". Bo trochę wcześniej była mowa o tym, że zgodnie z prawem zachowania energii rozpędzana cząstka może uzyskać dokładnie tyle samo energii, ile tej energii straci cząstka, która przyczyniła się do wzrostu prędkości poprzedniej cząstki. W tym przypadku są to "porównywalne" wielkości energii. Ale w tym przypadku następuje bezpośrednie wzajemne przyśpieszanie się cząstek i wzajemne przekazywanie sobie przez te cząstki energii. I, co jest szczególnie ważne, podczas rozpatrywania zagadnienia jest porównywana energia, jaka została utracona (przez jedną cząstkę), z energią, jaka została pozyskana (przez drugą cząstkę). Ale oprócz tego porównywana jest energia jednej i tej samej cząstki, jaką ta cząstka uzyskała lub przekazała w trakcie oddziaływania podczas różnych epizodów, przy różnych względnych prędkościach.
Sytuacja z wzajemnym bezpośrednim oddziaływaniem cząstek ze sobą jest prosta. Ale w przypadku akceleratorów sytuacja jest zupełnie inna. Jest ona właśnie taka, że aby uzyskać porównywalne ze sobą przyrosty energii przyśpieszanych cząstek, jakie mogą być uzyskane przy znacznie różniących się od siebie prędkościach cząstek, trzeba włożyć w ten proces nieporównywane większe ilości energii, aniżeli wynoszą przyrosty energii cząstek. Ta "nieporównywalność" energii w przypadku akceleratora bierze się stąd, że przekazywanie energii nie odbywa się w sposób bezpośredni (jak w przypadku oddziaływania ze soba cząstek), lecz za pośrednictwem złożonego procesu (czy mechanizmu) wytwarzania, przetwarzania i przekazywania energii przyśpieszanym cząstkom. Część energii, jaka jest tracona w akceleratorze i przekazywana cząstkom, jest oczywiście porównywalna z energią, jaką cząstki wskutek przyśpieszenia uzyskują. Ale nieporównywalnie wielka ilość energii podczas tego złożonego procesu wytwarzania, przetwarzania i przekazywania jest tracona i ulatuje w przestrzeń.
Zatem w rzeczywistości, gdy obecnie fizycy relatywiści, którzy z oczywistych względów jeszcze nie znają prawa znikomego działania, nieświadomie wiążą duże zużycie energii w akceleratorach ze wzrostem masy rozpędzanych do coraz większych prędkości cząstek, to w swojej interpretacji przedstawiają rodzaj usprawiedliwienia dla dużego zużycia energii.
Bogdan Szenkaryk "Pinopa"
Polska, Legnica, 2014.01.22.
Jestem wszystkim, wszędzie i zawsze. I wy wszyscy - także, tylko jeszcze o tym nie wiecie. Odkryjcie to na http://pinopa.narod.ru/Polska.html. Przekazuję prośbę od Łukasza - lukasz@lukasz.sos.pl : Bardzo proszę o 1,5 procent, Was nic nie kosztuje poza wypełnieniem dwóch pól w zeznaniach PIT, a mi ratuje życie. Proszę przekażcie ulotki swoim znajomym. Darowizny: FUNDACJA AVALON - Bezpośrednia Pomoc Niepełnosprawnym 62 1600 1286 0003 0031 8642 6001 BNP PARIBAS Fortis Bank Polska S.A. Bardzo ważny jest dopisek: SOSNA,711 (1,5%) Podatek: KRS: 0000270809 Bardzo ważny jest dopisek: SOSNA,711 PS. Jeżeli znacie firmę, która jest gotowa umieścić mój baner na swojej stronie z przekazaniem 1,5%, również proszę o kontakt. BARDZO DZIĘKUJĘ http://lukasz.sos.pl
Nowości od blogera
Inne tematy w dziale Technologie

