Po przyciężkawych tekstach dotyczących różniczkowania, pora na odpoczynkowy o dodawaniu lokalizacji Warszawy do lokalizacji Poznania.
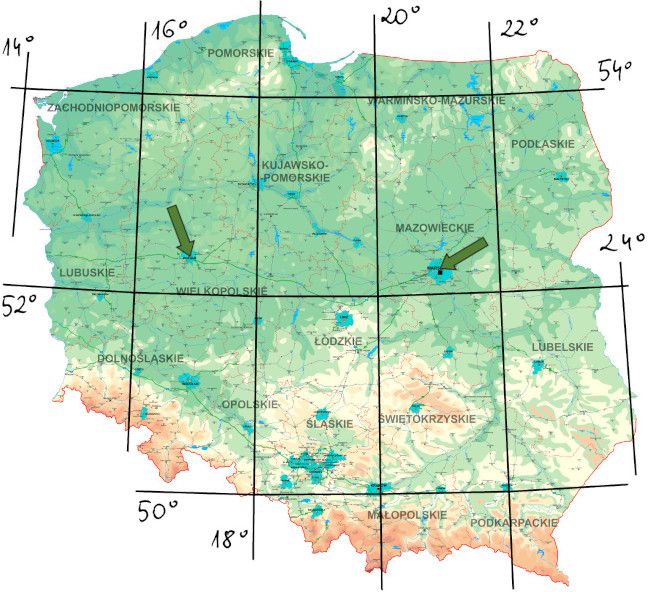
Obrazek przedstawia mapkę Polski z zaznaczonymi oboma miastami (i wybranymi poziomicami funkcji tworzących układ współrzędnych). Współrzędne punktów na mapach geograficznych podawane są w jednostkach długości i szerokości geograficznej. To po prostu dwie liczby – no bo każdy kawałek powierzchni naszej planety (z wyłączeniem południka 180), może być opisywany przez przyzwoity podzbiór R2. Korzystając z wiodącego serwisu internetowego, odczytałem (w pewnym przybliżeniu) pary oznaczające lokalizację centrum Poznania: (52,41; 16,93) i Warszawy: (52,23; 21,01). Liczby, jak to liczby, można do siebie dodać i wyniku… nie odnajdziemy już na globusie.
Przypatrzmy się nieco łatwiejszemu problemowi, jakim jest lokalizacja punktów w przestrzeniach niepozakrzywianych. W przeciwieństwie do „krzywej” powierzchni naszej planety, która przecież – jak pokazują najnowsze odkrycia geograficzno-astronomiczne – płaska nie jest.
Użyjmy na przykład liczb na osi liczbowej do przedstawienia drogi, jaką hipotetyczny kierowca przebywa między obecną, a byłą stolicą Polski.

Liczby – bo nimi są punkty osi liczbowej – można dodawać, mnożyć itd. Ale czy jest sens dodawać liczby odpowiadające lokalizacji konkretnych miast? Jakoś to głupio wygląda. Sens jest za to w odejmowaniu – w wyniku dostaniemy odległość między tymi miastami. Jednak sami przyznacie – co to za zbiór, gdzie można odejmować, ale dodawać już nie wypada…
No to pożartowaliśmy, pora na chwilę powagi.
Wektor wodzący
Z powodu wygody (prostoty, łatwości odbioru…) fizycy często, opisują położenie za pomocą wektora. No bo trzy współrzędne, to trzy liczby; a trzy liczby, to wektor jak się patrzy. Nazywają go nawet wektorem położenia albo wektorem wodzącym.
Ale to „coś” nie ma własności wektora wymaganych przez fizykę z dość zasadniczego powodu. Otóż dodawanie położeń jest dziwne. Położenie czego otrzymamy, gdy dodamy położenie Wrocławia do położenia Łodzi? Formalnie nawet możemy takie działanie zrobić, ale wynik zależy od układu współrzędnych, a w szczególności od tego, gdzie jest początek układu. Argument sformułowany bardziej ściśle brzmi: współrzędne takich wektorów transformują się dziwnie przy zmianie układu.
No dobrze, uspokoję czytelników – to nie jest tak, że przez kilkaset lat nikt nie zauważył niepokojących cech modelu. Problem rozwiązano wprowadzając tzw. przestrzeń afiniczną. Pomysł polega na tym, że zbiór punktów – nawet jeśli jest przykładnym podzbiorem Rn – jest tylko zbiorem punktów. Do zbioru dołączamy za to odpowiednią przestrzeń wektorową. Każde dwa punkty zbioru wiąże się z jakimś wektorem – te dwa punkty to coś, co zwykle nazwa się początkiem i końcem wektora. Czyli mamy coś w rodzaju „odejmowania punktów”.
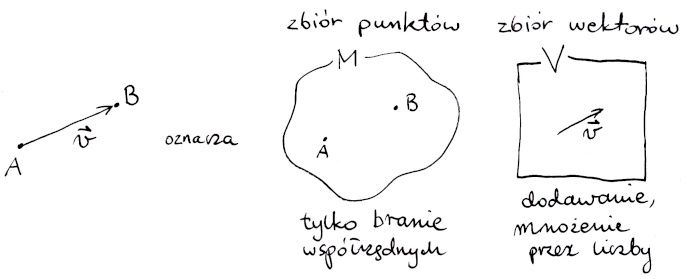
Przestrzeń afiniczna to najprostsza wersja, dość typowej procedury postępowania z Rn lub jej ładnymi podzbiorami. Polega ona na tym, że „zapominamy” o bonusach wypisanych w notce „Matematyka R×R×…R”, zostawiając funkcjonalność układu współrzędnych, a potrzebne treści umieszczamy w dodatkowych strukturach. Czasami będą zgodne z bonusowymi, a czasami nie.
Mniej trywialny przykład w następnym odcinku.







Komentarze
Pokaż komentarze (13)