MM&AlK
Szyfry (4). I tylko to…
Przykłady omówione w notkach wcześniejszych mówią, dlaczego rząd USA odstąpił od wykorzystywania szyfrowania algorytmem RSA… Mówią, że dla celów szyfrowania wykorzystywane są generatory liczb pierwszych a nie liczb losowych, jak to się powszechnie pisze. Zatem wszystkie klucze publiczne skażone są ingerencją człowieka w zasady ich znajdowania. Tak więc ingerując w algorytm kreowania liczb pierwszych wiemy jak taki klucz publiczny złamać. Korzystając z programów szyfrujących, oddajemy nasze poufne dane w ręce firm (ludzi), którzy ustalają zasady generowania tych liczb. Na to rząd USA nie wyraził zgody…
W czasach współczesnych obserwujemy wiele włamań na serwery urzędów czy też firm prywatnych. Nie należy się dziwić. Istnieje wiele programów dających sobie doskonale radę z rozkładem dużych liczb postaci 2a + 1 np. przytaczany SageMath przeznaczony dla szkół, doskonale radzi sobie z rozkładem liczb 245 bitowych w ciągu paru sekund. Poniżej przykład takiego rozkładu liczby o 81 cyfrach…
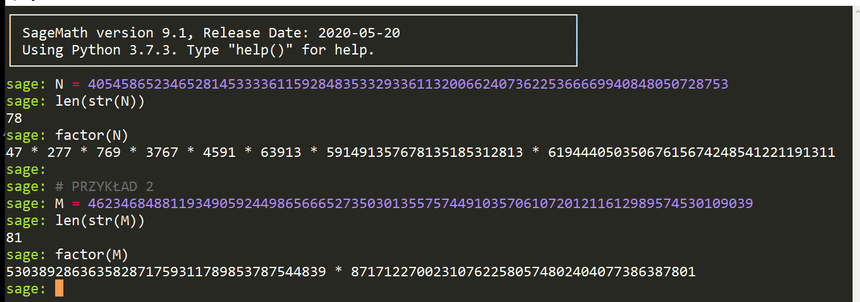
Lub 509 bitowej liczby Mersenne’a, mającej 154 cyfry
M = 2509 – 1 = a × b × c × d =16759759912428246374467531247757307659349207275740
4917221544518046522050375919337210023428727086292846125398227331075635671
9235351493321243304206125760511, gdzie:
a = 509 × 24792 + 1,
b = 509 × 37503889676080358 + 1,
c = 509 × 1271366828376984040784 + 1,
d = 509 × 2112213809041678983548124969026393940998264802805865000734080631035
6832970631328083378297905926205352 + 1.
… A co można powiedzieć o możliwościach super komputerów Chińskich, Amerykańskich czy też Rosyjskich mających miliardy T-bajtów pamięci?…
A na koniec najciekawsza i bardzo zwodnicza metoda faktoryzacji – metoda kolejnych przybliżeń...
Spytano P. Fermata czy liczba N = 100 895 598 169 jest liczbą pierwszą. Fermat zaprzeczył podając rozkład liczby N na czynniki pierwsze. W wielu podręcznikach i publikacjach zadawane jest pytanie jak to zrobił... Nie było kalkulatorów, komputerów, matematyka w „powijakach”… Zatem jak to zrobił?
Liczbę N pogrupujemy: 1008 9559 8169. Dwie pierwsze cyfry liczby N (liczba 10) mówią, że pierwsza cyfra czynników iloczynu, to dla liczby B > A jest: 4, 5, 7, 8, 9, natomiast dla liczby A: 1, 2, 3. Zaczniemy od cyfr krańcowych. Szukamy takich liczb dwucyfrowych, których iloczyn zbliżony jest do liczby 1 008. Dla liczby B z pierwszą cyfrą 9 i liczby A z pierwszą cyfrą 1, mamy:
91 × 11 = 1 001... Dalsze rozwinięcie doprowadzi do błędu.
Dla liczby B z pierwszą cyfrą 8 i liczby A z pierwszą cyfrą 1, mamy: 89 × 11 = 979.
(89 × 12 = 1 068 > 1 008). Zatem B = 89..., A = 11... Mamy po dwie pierwsze cyfry liczb A, B.
Do cyfr liczb A, B dopisujemy po dwie cyfry takie, aby iloczyn liczb tak utworzonych był zbliżony do liczby 10089559.
Sprawdzając iloczyny od liczb 8901 × 1134 dojdziemy do liczby 8984 × 1123 = 10089032.
Pierwsze cztery cyfry liczb A, B, to B = 8984... i A = 1123... .
Do cyfr liczb A, B dopisujemy po dwie cyfry takie, aby iloczyn liczb tak utworzonych był równy liczbie N = 10089598169. Sprawdzając iloczyny od liczb 898421 × 112301 dojdziemy do liczby:
898 423 × 112 303 = 1 008 9559 8169 = N.
Przykład 2.
Dana jest liczba N = A × B = 148 998 061. Znaleźć czynniki iloczynu wiedząc, że liczby A, B mają różne ilości cyfr.
Liczba N posiada nieparzystą ilość cyfr. Rozpoczynamy zatem od trzech pierwszych cyfr. Najbliższym przybliżeniem iloczynu liczb do liczby 148 jest iloczyn liczb
10 × 14 = 140. Pierwsze dwie cyfry liczby A, to 10.., a liczby B..., to 14.
Dzieląc liczbę N osobno przez 10 i 14 otrzymujemy liczby zmiennoprzecinkowe. Wracamy do liczb.
Najbliższym przybliżeniem iloczynu liczb do liczby 14 899 jest iloczyn 143 × 104 = 14 872.
Iloczyn 142 × 105 = 14 910 > 14 899; Przyjmujemy zatem iloczyn 142 × 104 = 14 768.
Pierwsze trzy cyfry liczby A, to 104.., a liczby B..., to 142.
Dzieląc liczbę N osobno przez 104 i 142 otrzymujemy liczby zmiennoprzecinkowe. Wracamy do liczb.
Najbliższym przybliżeniem iloczynu liczb do liczby 1489980 jest iloczyn
1047 x 1423 = 1 489 881. Pierwsze cztery cyfry liczby A, to 1047.., a liczby B..., to 1423.
Dzieląc liczbę N osobno przez 1047 i 1423 dla liczby B otrzymujemy liczbę całkowita A:
A = N/B = 148 998 061/1 423 = 104 707.
A = 104 707, B = 1 423.

