MM&AlK
Trójkąt pitagorejski i koło.
Dowód Möllmanna
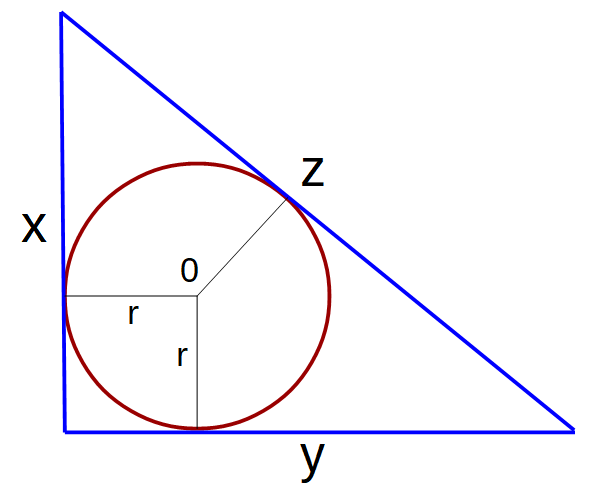
Promień r koła wpisanego w trójkąt wynosi: r = (x + y – z)/2
Obwód v trójkąta wynosi: v = (x + y + z)/2
Pole p trójkąta wynosi: p = xy/2 = vr
Jest więc: 2xy = (x + y)2 – z2 stąd: z2 = (x + y)2 – 2xy ; ostatecznie: z2 = x2 + y2
Trójkątom pitagorejskim wiele uwagi poświęcił W. Sierpiński w monografii Trójkąty pitagorejskie. Z wielu udowodnionych twierdzeń przedstawiamy tylko dwa, którym to twierdzeniom poświęcimy szczególną uwagę.
Twierdzenie 1. (W. Sierpiński Teoria liczb cz. II, str. 52) W każdym trójkącie pitagorejskim promień koła wpisanego wewnętrznie, jako też promienie każdego z trzech kół, wpisanych dla tego trójkąta zewnętrznie, są liczbami naturalnymi.
Czyli: Dla każdej liczby naturalnej r istnieje trójkąt pitagorejski pierwotny, w którym koło wpisane ma promień r.
Twierdzenie 2. V.A. Lebesgue’a (W. Sierpiński Teoria liczb cz. II, str. 58). Jeżeli wielkie twierdzenie Fermata jest prawdziwe dla wykładnika n, to nie ma trójkąta pitagorejskiego, którego obie przyprostokątne byłyby n-tymi potęgami liczb naturalnych. Jest to więc w każdym razie prawdą dla wszystkich naturalnych n ≤ 4001.
Parę słów własnych o kole wpisanym w trójkąt…
Dla klasycznych trójkątów pitagorejskich o bokach x, y, z spełniających równanie:
x2 + y2 = z2
gdzie x, z są liczbami naturalnymi nieparzystymi promień r koła wpisanego w ten trójkąt wynosi:
(x + y – z)/2 = [x – (z –y)]/2 = r
Możemy dowieść, że dla klasycznych trójkątów pitagorejskich zachodzi również zależność:
[(z – x)/2]1/2 = r
Czyli: Promień r koła wpisanego w trójkąt jest równy pierwiastkowi z połowy różnicy liczb nieparzystych (przeciwprostokątnej z i przyprostokątnej nieparzystej x).
Stąd: 2r2 = z – x
Dowód możemy przeprowadzić na kilka sposobów. Oto jeden z nich:
Założenie. Przyjmujemy, że mamy trójkąt pitagorejski, którego przeciwprostokątna z i jedna z przyprostokątnych np. x są liczbami naturalnymi nieparzystymi.
Twierdzenie. W trójkącie prostokątnym, w którym przeciwprostokątna i jedna z przyprostokątnych są liczbami naturalnymi nieparzystymi, podwojony kwadrat promienia r koła wpisanego w ten trójkąt, jest liczbą naturalną równą różnicy tych liczb.
Inaczej mówiąc: W trójkącie pitagorejskim wielkość promienia r koła wpisanego w ten trójkąt jest pierwiastkiem z połowy różnicy liczb nieparzystych.
Dowód.
1o Trójkąty pitagorejskie pierwotne.
Z zależności: [(z – x)/2]1/2 = r otrzymujemy: r2 = (z – x)/2 ; 2r2 = z – x.
Z zależności: [x – (z – y)]/2 = r otrzymujemy: y – (z – x) = 2r,
Wobec z – x = 2r2 mamy: y – 2r2 = 2r stąd: y =2r2 + 2r = 2r(r + 1).
Z zależności: [(z + x)/2]1/2 = r + 1 otrzymujemy:
(r + 1)2 = (z + x)/2 ; 2(r + 1)2 = z + x
zatem: z = (r + 1)2 + r2 ; x = (r + 1)2 – r2 ; y = 2r(r + 1)
Podstawiając odpowiednio x, y, z do równania: x2 + y2 = z2 otrzymujemy:
[(r + 1)2 – r2]2 + 4r2(r + 1)2 = [(r + 1)2 + r2]2 c.b.d.o.
Otrzymane zależności dotyczą trójkątów klasycznych pitagorejskich…
2o Trójkąty pitagorejskie dowolne.
W trójkątach pitagorejskich dowolnych o bokach:
x = m2 – n2, y = 2mn, z = m2 + n2
liczbę m > n możemy zapisać w postaci: m = n + k gdzie k jest liczbą naturalną. Boki trójkąta wynoszą wówczas:
x = (n + k)2 – n2, y = 2n(n + k), z = (n + k)2 + n2.
Interpretacja zależności w trójkątach prostokątnych, wyrażonych wzorami powyżej, jest bardzo ciekawa... Dla trójkątów zachodzi zależność:
(x + y – z)/2k = [(z – x)/2]1/2
Mamy bowiem dla prawej strony równania:
[(z – x)/2]1/2 = {[(n + k)2 + n2 – (n + k)2 + n2]/2}1/2 = n
Stąd: z – x = 2n2.
Dla strony lewej natomiast:
(x + y – z)/2k = [(n + k)2 – n2 + 2n(n + k) – (n + k)2 – n2 ]/2k = n
Stąd: (x + y – z)/k = 2n
gdzie n jest promieniem okręgu wpisanego w trójkąt n = r.
Zachodzi również: [(z + x)/2]1/2 = n + k.
3o Trójkąty pitagorejskie o wzorze ogólnym.
Dla trójkątów pitagorejskich o wzorze ogólnym:
[k(2r + k)]2 + [2r(r + k)]2 = [2r(r + k) + k2]2
gdzie: k, r są liczbami naturalnymi, o bokach:
x = k(2r + k) ; y = 2r(r + k) ; z = 2r(r + k) + k2 = 2r2 + k(2r + k)
wobec zależności: (x + y – z)/2k = [(z – x)/2]1/2 mamy dla strony lewej równania:
[k(2r + k) + 2r(r + k) – 2r2 – k(2r + k)]/2k = r.
Dla prawej strony równania jest natomiast:
{[2r2 + k(2r + k) – k(2r + k)]/2}1/2 = r.
Teraz finał…
Analizując zależności powyżej możemy zauważyć, że twierdzenie V.A. Lebesgue’a możemy znacznie rozbudować wykorzystując zależności geometryczne…
Przyjmujemy w założeniu, że dane są potęgi liczb naturalnych xn, am, względnie pierwszych, z których jedna jest liczbą parzystą a druga nieparzystą. Tradycyjnie przyjmiemy, że liczba x, jest liczbą nieparzystą, natomiast a jest liczbą parzystą. Przyjmiemy również, że wykładniki potęgowe n, m są dowolnymi liczbami nieparzystymi n, m > 1.
Suma liczb xn, am wynosi: xn + am = zt
gdzie n, m > 1 oraz t jest liczbą całkowitą t = 1, 2, 3, ... n, ... (n + k);
stąd: zt – xn = am
Twierdzimy: Równanie: (1) x2n + y2n = z2t
nie ma rozwiązania w liczbach naturalnych dla zt = xn + am
gdzie n, m > 1 oraz t jest liczbą całkowitą t = 1, 2, 3, ... n ... (n + k)
Dowód.
Równanie (1) jest klasycznym równaniem pitagorejskim: (xn)2 + (yn)2= ( zt)2
W trójkątach pitagorejskich promień r okręgu wpisanego w trójkąt jest liczbą naturalną i jest pierwiastkiem z połowy różnicy przeciwprostokątnej i przyprostokątnej nieparzystej.
r = [(zt – xn)/2]1/2
Jest więc: zt – xn = 2r2 = am zatem r2 = am/2. Liczba am/2 nie jest kwadratem liczby naturalnej. Promień okręgu wpisanego w trójkąt nie jest liczbą naturalną.
Wobec: yn = 2r(r + k)
przy promieniu r nie będącym liczbą naturalną yn nie jest liczbą naturalną. Zatem przyprostokątna parzysta nie jest n-tą potęgą liczby naturalnej
W rzeczy samej wobec 2r2 = am mamy:
yn = 2r(r + k) = 2r2 + 2rk
stąd: yn = am + 2k(am/2)1/2
Zatem równanie: x2n + y2n = z2t nie ma rozwiązania w liczbach naturalnych.
Wykazaliśmy więc, że nie istnieje trójkąt pitagorejski, którego obie przyprostokątne są n-tymi potęgami liczb naturalnych jeżeli przeciwprostokątna jest sumą potęg liczb naturalnych o wykładnikach n, m będącymi dowolnymi liczbami nieparzystymi n, m > 1.
Czytelnik, który przeanalizował wszystkie notki Tajemnic Pitagorasa nie będzie miał problemu aby geometrycznie udowodnić Wielkie Twierdzenie Fermata dla wykładników parzystych. Dowód matematyczny przeprowadził w roku 1971 Terjanianiun. Dowód oparty jest na twierdzeniu: Niech p będzie liczbą pierwszą nieparzystą. Jeżeli niezerowe liczby całkowite x, y, z spełniają
x2p + y2p = z2p, to 2p dzieli x lub y... Co daje sprzeczność...
Inne tematy w dziale Technologie

