Mgły, liczby zespolone, linie i koła

Samolot na dębie wisi
W okaleczeniach licznych.
Otoczyły go liście, jak gapiowie cisi,
Jak dobra publiczność - - -
Mgła rozdziera szaty na sosnach,
Winowajczyni żałosna.

Maria Pawlikowska-Jasnorzewska, „Śpiąca załoga” 1933

No tak, nie samolot to a wrony, no i nie na sosnach. Ale mgła jest, autentyczna.

I tak było dzisiejszego ranka, i tak jest dzisiejszego wieczoru. Dzień miał być teoretycznie słoneczny. I zapewne był, ale nie u mnie. Zbyt blisko mnie płynie rzeka Garonna.

To przez tę bliskość rzeki słońca u mnie o wiele mniej niż w odległej o 70 km Tuluzie

Teoretycznie miałem pisać o potokach pół wektorowych. Z potoku zrobiła się rzeka, z rzeki zrobiła się mgła, a z mgły wypłynęło koło uczniowskie i liczby zespolone. I dzielenie okręgu na równe części. A potoki pól wektorowych będą – nie uciekną.

W liceum na kole będą na pewno liczby zespolone. A może już były? Takie jak z=1+2i. Licealista nauczy się mnożyć (1+i)(1+2i). Nauczy się dzielić (1+i)/(1+2i). Dowie się, że są liczby sprzężone – sprzężona do 1+i to 1-i, przekona się, że iloczyn liczby przez liczbę sprzężoną jest liczbą rzeczywistą, nieujemną. Co pomoże licealiście w dzieleniu i w obliczeniu ile to jest (1+i)/(1+2i).

Liczby zespolone to algebra. Ale blisko jest geometria. Liczbę zespoloną przedstawiamy jako punkt na płaszczyźnie (x,y). Liczbę 1+2i przedstawiamy jako punkt x=1,y=2.

Zadanie; przy użycia cyrkla i linijki narysowć n-kąt formny wpisany w okrąg. Da się to zrobić czy nie?

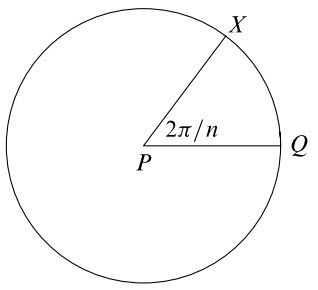
Dla n=6 każdy chyba to potrafi.

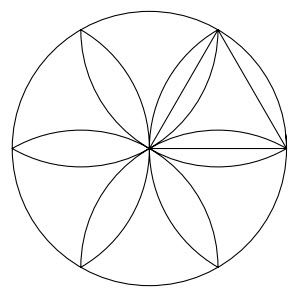
A dla innych n? Siedmiokąt? Do dziś nie wiedziałem jak na to pytanie odpowiedzieć. Ale życie zmusiło mnie do zabrania się do nauki o polach skończonych (każdy specjalista od kryptografii to wie, a ja nie mam o tym pojęcia). I trafiłem na taki problem, który niniejszym podaję. Będziemy go razem rozwiązywać.

Mamy najpierw oznaczenia: R²  - płaszczyzna rzeczywista, C – płaszczyzna zespolona (niby to samo, ale w R² rysujemy pary liczb rzeczywistych, zaś w C rysujemy punkty reprezentujące liczby zespolone.

Powiedzmy, że M to jest jakiś zbiór punktów płaszczyzny. Przez CyrL(M) oznaczmy zbiór tych wszystkich punktów, które można otrzymać z M przy pomocy cyrkla i linijki. Te punkty konstruujemy na trzy elementarne sposoby. Niech

Li(M) – zbiór prostych łączących punkty M
Ci(M) zbiór okręgów o środkach w punktach M

Nowe punkty mogą powstać przez: przecięcie dwóch linii z Li(M), przez przecięcie okręgu z Ci(M() z linią z Li(M), przez przecięcie dwóch okręgów z Ci(M).

Zadanie: Niech M będzie zbiorem punktów na płaszczyźnie do którego należą liczby 0 i 1. Udowodnić, że

1) i należy do CyrL(M)
2) Jeśli z należy do CyrL(M) to z sprzężone też należy do CyrL(M)
3) Jeśli z =x+iy należy do CyrL(M) to x i y (część rzeczywista i urojona liczby z) należy do CyrL(M)
4) Jeśli z należy do CyrL(M) to -z też należy do CyrL(M)
5) Jeśli z i z' należą do CyrL(M) to z+z' też należy do CyrL(M)
6) Jeśli z i z' należą do CyrL(M) to zz' też należy do CyrL(M)
7) Jeśli z należy do CyrL(M) i z nie jest zerem, to 1/z też należy do CyrL(M)

Jak tego dowieść? Pewne punkty wydają się łatwe, inne trudniejsze. W sam raz na koło. A ja zabieram się do kontynuowania nauki. Chcę rozgryźć ten eksponencjał  dla pól skończonych.