Stawianie hipotez to sztuka. Ich potwierdzanie lub obalanie, to inny rodzaj sztuki. Hipotezy nie są wynikiem rozumowania indukcyjnego. Po prostu coś nas "oświeca". Skądś wiemy, że "coś może być prawdą". Często łatwiej hipotezę postawić niż ją sprawdzić. Tak jest do dziś ze słynną hipotezą Riemanna.
Ta notka jest poświęcona przykładowi. Jak postawiłem hipotezę. Rzecz wzięła się ze spostrzeżenia Bjaba pod poprzednią notką. W pracy Białynickich "The role of the Riemann-Silberstein vector in classical and quantum theories of electromagnetism" znajdujemy formułę na zespolony wektor e(k) o normie 1
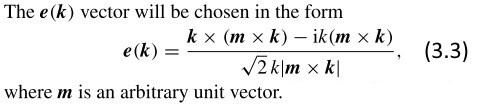
Zależy on od dowolnego wektora m (byle nie równoległego do k) rzeczywistego o normie 1. Oznaczmy więc go raczej e(m,k) miast e(k). Wektor ten jest wektorem własnym operatora skrętności Λ(k) do wartości własnej +1. Podprzestrzeń wektorów własnych należących do tej wartości własnej jest jednowymiarowa. Wynika stąd, że wektory e(m,k) i e(m',k) dla dowolnych jednostkowych m i m' muszą być współliniowe.
Musi zatem być e(m',k) =c e(m,k). Ponieważ oba wektory e(m,k) i e(m',k) mają normę 1, stała c musi być liczbą zespoloną o module 1. Jest zatem postaci
c = e-i ϕ = cos(ϕ) - i sin(ϕ)
gdzie ϕ jest kątem pomiędzy 0 a 2 pi. Ten kąt będzie na ogół zależał od m,m',k. Zapiszmy więc
e(m',k) = e -i ϕ(m,m',k) e(m,k)
Co to za kąt, ten ϕ(m,m',k)?
Moja hipoteza: ϕ(m,m',k) jest kątem pomiędzy wektorami mxk i m'xk.
Dokładniej: kąt o jaki należy obrócić wektor mxk wokół osi k by otrzymać m'xk.
Mamy więc jasną i jawnie postawioną hipotezę. Trzeba ją sprawdzić. Można sprawdzać ręcznie algebraicznie, można sprawdzać numerycznie. Można użyć programu Mathematica. Można używać tożsamości z Wikipedii. Jest zatem praca do wykonania. Potwierdzić lub obalić moją hipotezę. Czy ktoś się tej pracy podejmie?
------------------
Dodane 3-05-22 rankiem
Nie mogłem jakoś spać i sobie w nocy hipotezę udowodniłem. Oto mój dowód. Może trochę skrótowy, ale powinien być dobry. Najpierw dwie wstępne obserwacje. Pierwsza: Jeśli weźmiemy dowolny obrót R reprezentowany przez macierz ortogonalną o wyznaczniku 1, jeśli obrócimy tą macierzą wektory k,m,m' to kąt pomiędzy wektorami mxk i m'xk się przy tym nie zmieni, zaś zespolone wektory e(m,k) i e(m',k) obrócą się przez tę samą macierz R i współczynnik c się przy tym nie zmieni.
e(Rm,Rk)=Re(m,k), e(Rm',Rk)=Re(m',k)=Rce(m,k)=cRe(m,k) = ce(Rm,Rk)
Druga obserwacja: jeśli przeskalujemy wektor k, to oba wektory e(m,k) i e(m',k) przeskalują się tak samo i współczynnik proporcjonalności c się nie zmieni. Ani nie zmieni się kąt pomiędzy mxk i m'xk
Z tych dwóch obserwacji wynika, że bez zmniejszania ogólności możemy wybrać układ współrzędnych tak by
k=(0,0,1),
mxk=(1,0,0),
kx(mxk)=(0,1,0).
Innymi słowy mxk to wektor jednostkowy wzdłuż osi x, kx(mxk) - wektor jednostkowy wzdłuż osi y, k - wektor jednostkowy wzdłuż osi z.
Przy powyższym wyborze i ustawieniu osi możemy teraz z łatwością znaleźć wektor e(m,k). Jeśli się nie pomyliłem to mamy
e(m,k) = ( -i, 1, 0 ) / √ 2
Zajmijmy się wektorem e(m',k). Wektor m'xk jest prostopadły do k, leży zatem w płaszczyźnie x,y. Ma zatem składowe
m'xk=(cos ϕ, sin ϕ, 0) gdzie ϕ jest kątem o jaki należy obrócić wersor osi x (czyli wektor mxk) by otrzymać m'xk.
Możemy z łatwością obliczyć wektor e(m',k).
e(m',k) = ( - sin ϕ - i cos ϕ, cos ϕ - i sin ϕ , 0)/√ 2
I widać od razu, że
e(m',k) = exp (-i ϕ) e(m,k)
Jak w hipotezie
CBDO
Quod Erat Demonstrandum
A hipoteza i dowód zawdzięczają swe istnienie niezmierzonej ciekawości Bjaba i bezgranicznemu entuzjazmowi Kleopatry.







Komentarze
Pokaż komentarze (88)