„Huczą słońca grzmiących trąb,
Kołujący rośnie krąg,
Pędzi zawrót
kolisty
Po elipsie
falistej,
Jednomętnym rozpływem wiruje jak bąk.) „
No, kto to napisał, kto?
Łatwe? A to od kogo pochodzi:
A oto Wofgang Pauli (ten, co odkrył spin) i Niels Bohr (ten, który wyprał mózgi fizyków doktryną komplementarności) jako te dzieci pochylają się nad wirującym bąkiem...

W poprzedniej nocie zadałem pytanie: ile jest okręgów stycznej do prostej w danym punkcie? Odpowiedział waldemar.m. Jego odpowiedź brzmiała: „jeden”.
No to popatrzmy:
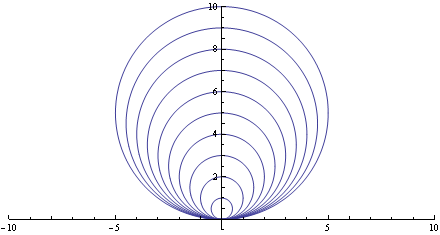
Prosta, tutaj po prostu oś x, jest styczna do tych wszystkich okręgów w punkcie x=0,y=0. Wszystkie te okręgi są zatem styczne do prostej w tym punkcie. Oczywiście powiedzielibyśmy, że „czym większy jest promień okręgu, tym bardziej jest on styczny do naszej prostej.” Jak śpiewał Kubuś Puchatek: „Im bardziej pada śnieg, tym bardziej pada śnieg ...” Puchatek Puchatkiem, ma swoją puchatkową rację, a jednak wszystkie te okręgi są styczne do naszej prostej. Zatem prawidłowa odpowiedź na moje pytanie brzmi: nieskończenie wiele.
No dobrze, ale prosta to coś wyjątkowego. A jak to będzie jeśli prostą zastąpimy czymś nieco bardziej skomplikowaną, na przykład parabolą? Popatrzmy. Weźmy parabolę. Najprostsza parabola to y=x2, ale ja wolę (dlaczego, to, póki co, moja słodka tajemnica) parabolę opisaną równaniem
y = (x2 + 1)/2
Jej wykres wygląda tak:
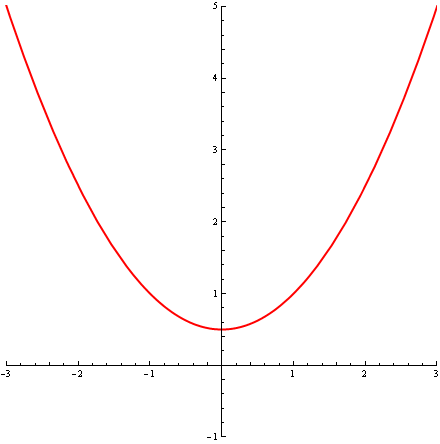
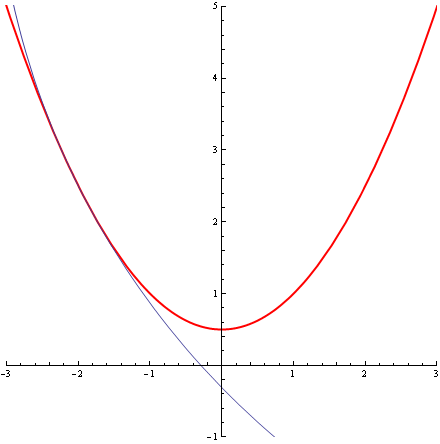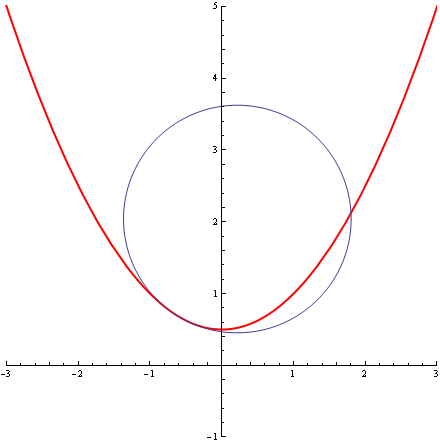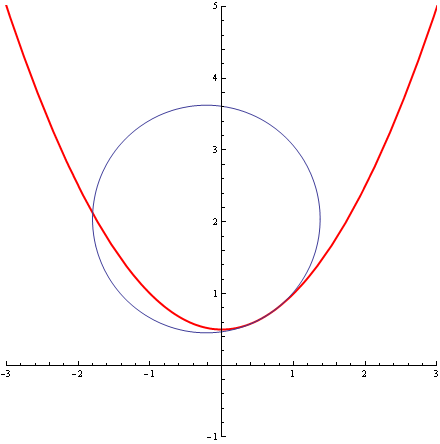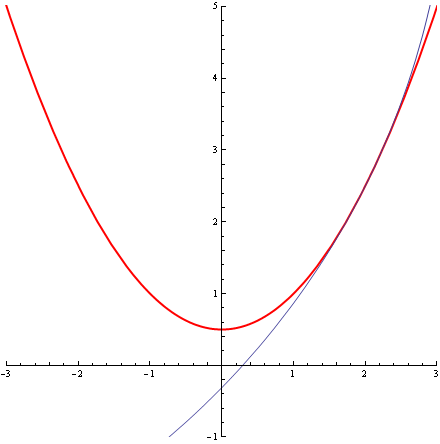
Przyjrzyjmy się teraz kilku okręgom stycznym do tej paraboli w jej wierzchołku, okręgom o promieniach, od najmniejszego do największego, ¼, ½, 1, 2, 3:
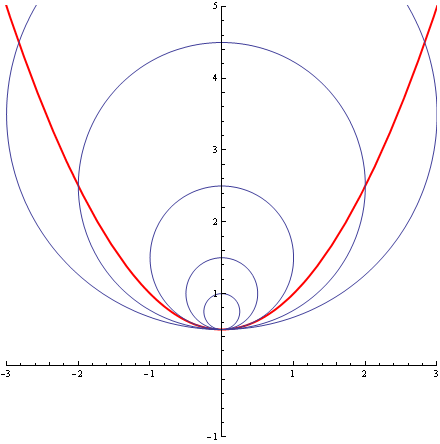
Wszystkie są styczne do paraboli w jej wierzchołku, a jednak jeden z nich jest „bardziej styczny” od wszystkich pozostałych – charakteryzuje go styczność „drugiego rzędu”. To ten okrąg środkowy, o promieniu R=1. Ten to wręcz „całuje” parabolę. I tak sie to, jak to już tichy zauważył, nazywa. Nazywa się go „osculating circle”. Dla każdej „porządnej krzywej”, w prawie każdym punkcie p tej krzywej istnieje taki jeden i tylko jeden całujący ta krzywą w tym punkcie p okrąg o pewnym promieniu R. Odwrotność wartości tego promienia nazywa się krzywizną (zewnętrzną) krzywej w punkcie p. Krzywizna naszej paraboli z przykładu, w jej wierzchołku, wynosi 1.
Filmik-animację z okręgiem całującym parabolę można zobaczyć tutaj. Tam też można zobaczyć animację oskulujacego okręgu całującego krzywą y = x3. Dla tej krzywej, w punkcie x=0,y=0, nasz okrąg ma mały problem, bo dla x ujemnych całuje krzywą z jednej strony, zaś dla x dodatnich – z drugiej strony. Dla x=0 nie może się zdecydować z której strony ma całować, zresztą pojawia się dodatkowy problem, że jego promień staje się nieskończony a krzywizna staje się zerem. Całowanie może więc przynieść niespodzianki.
Dla programistów jestem winien formułę. Otóż, jeśli krzywa sparametryzowana dana jest równaniami (x(t), y(t)), to krzywizna kappa(t), w punkcie odpowiadającym wartości t parametru dana jest wzorem
kappa(t) = licznik/mianownik
gdzie
licznik = x' y'' – y'x''
mianownik = (x'2 + y'2)3/2.
Środek (a(t),b(t)) oskulujacego okręgu dany jest zaś wzorem
a(t) = x(t) - licznik_a/mianownik, b(t) = y(t) + licznik_b/mianownik
licznik_a = y'(t)(x'(t) 2 + y'(t)2 )
licznik_b = x'(t)(x'(t)2 + y'(t)2)
mianownik (w obu przypadkach ten sam) = x'(t)y''(t) – y'(t)x''(t)
Przez prim oznaczyłem pochodną po parametrze.
Korzystając z tych wzorów zrobiłem moją własną małą animację okręgu tulącego się do mojej paraboli. Oto ona:
Pozostaje pytanie (czy tylko jedno?): skąd się wzięły te wzory powyżej? Otóż wymyślili je matematycy, którzy niczego nie produkują poza dziwnymi formułami. A inżynierowie te formuły od matematyków z pocałowaniem ręki biorą i zamieniają na coś „użytecznego”. Mówiąc może nieco niesmacznie: na pieniądze. A serio: ze studiowania problemu „długości krzywej” i wektorów prędkości i przyśpieszenia.








Komentarze
Pokaż komentarze (36)