Z tajemnicami spotykamy się codziennie. Przechodzimy koło nich niby nic, nie zwracamy uwagi. A one tam są, ukryte w pełnym świetle. I tak to jest z efektem Dżanibekowa, którym ostatnio się zajmujemy. Ukrywa się w pełnym świetle. To efekt czysto mechaniczny. Ważne są są oba słowa: „czysto” i „mechaniczny”. Bo efekt jest, w samej rzeczy, bardzo czysty. Widoczny jak na dłoni. Dlatego przez tyle lat nikt nań nie zwrócił uwagi.
Mechaniki na studiach uczyłem się z podręcznika Landaua-Lifszyca

Czegoś tam się chyba musiałem nauczyć, bo w indeksie z egzminu mam piątkę, ale po egzaminie widocznie wszystko zapomniałem. W szczególności zapomniałem wszystko o bryle sztywnej. A może wykładowca uznał wtedy ten najciekawszy materiał za nieistotny? Nie wiem. Dziś, po latach, powrócę do tego podręcznika. Przespacerujemy się razem po odpowiednich fragmentach, odkryjemy to co jest tam ukryte … w pełnym świetle.
Przyjrzyjmy się pierwszemu wáznemu dla nas fragmentowi. Powinniśmy rozpoznać równania Eulera:
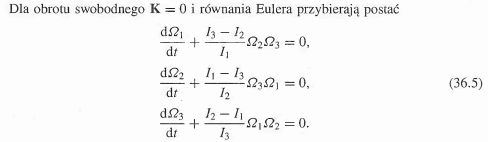
Prędkość kątowa w układzie związanym z ciałem oznaczona jest dużą literką Ω . Zamiast składowych x,y,z mamy indeksy 1,2,3. Momenty bezwładności względem osi głównych ciała to I1,I2,I3. Nasze ciało obraca się swobodnie, nie działają na nie żadne momenty sił. To właśnie nas interesuje. Tam gdzieś ukrywa się tajemnicze fikanie. Tylko gdzie? Jedziemy dalej:

Bąk niesymetryczny. To właśnie nas interesuje. Zakładamy, że
I3 > I2 > I1
No dobrze. Chcę zrobić jeden tylko przykład, wezmę I3 = 3, I2 = 2, I1= 1, tak jak czésto przyjmowaøem w poprzednich notkach. Trudno o coś prostszego. Zobaczymy, że fikająca gajka tu właśnie fika.
Nawet mechaniczny bąk niesymetryczny słucha się praw zachowania energii i krętu. Energia kinetyczna oznaczana jest tu literką E, wektor krętu literką M, jego długość to M. Wnioski z tych praw zachowania, przecięcia dwóch elipsoid, już dyskutowaliśmy w notce Elipsoidalne fikania. Jedziemy zatem dalej:

Opuszczam przy tym wiele. Chcę wybrać to co dla nas istotne. Widzimy, że w podręczniku ograniczają się do przypadku gdy M2 > 2 E I2. To mi się nie podoba. Chcę postawić ołówek na ostrzu, jak to ładnie opisał ZAKRĘCONY w komentarzu pod poprzednią notką. Nie będę się zatem tym ograniczeniem przejmował i na końcu wezmę M2 = 2 E I2. Bowiem wtedy efekt zobaczymy w pełnym świetle, jak na dłoni. Wezmę M2 = 10, E = 2.5 – tak jak to było w poprzedniej notce, Efekt motyla - Fiknie czy nie fiknie?
By móc użyć trego co jest w podręczniku, potrzebne nam będzie tau wyrażone przez t, ze wzoru (37.8), oraz k2 ze wzoru (37.9). k2 oblicza się łatwo – wychodzi
k2 = 1.
Natomiast ten pierwiastek kwadratowy w pierwszym wzorze (37.8) – (drugi nie będzie nam potrzebny) – wychodzi √(5/6):
tau = √(5/6) t.
I co dalej? Dalej u Landaua-Lifszyca jest to:
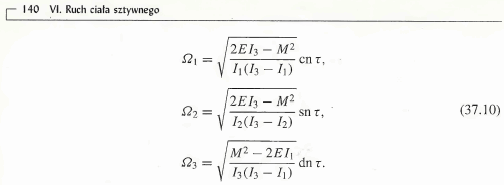
Mamy mianowicie jawne rozwiązanie równań Eulera!!! Po prawej stronie mamy współczynniki z pierwiastkami. Trzeba będzie je wyliczyć. Mamy też funkcje od tau: cn, sn, dn. Trzeba będzie je zidentyfikować.
Najpierw współczynniki. To łatwe. Wychodzą kolejno √(5/2) , √(5/2) , √(5/6).
Teraz te tajemnicze funkcje. Zaglądamy do Wikipedii pod Funkcje eliptyczne Jacobiego. I owszem, są tam funkcje cn, sn, dn tyle, że mają oprócz głównego argumentu jeszcze drugi argument: k2. Ale u nas k2 = 1. Pod sam koniec wpisu w Wikipedii znajdujemy:
sn(x,1) = tanh x
cn(x,1) = sech x
dn(x,1) = sech x
No to jesteśmy w domu. W naszym przypadku wzory z Landaua-Lifszyca dają:
Ω1(t) = √(5/2) sech (√(5/6) t)
Ω2(t) = √(5/2) tanh (√(5/6) t)
Ω3(t) = √(5/6) sech (√(5/6) t)
Proszę, proszę, wychodzi nawet to, co BJAB zauważył w komentarzu pod poprzednią notką: ωX^2 = 3 * ωZ^2. To właśnie tych funkcji wykresy robiłem w poprzedniej notce i w komentarzach do niej.
Póki co idzie nam dobrze. Na razie mamy prędkości kątowe w układzie ciała. A co z katami Eulera dającymi położenie bąka widziane z przestrzeni? Czytamy dalej:

Wybieramy zatem oś Z układu inercjalnego w przestrzeni wzdłuż wektora zachowanego krętu M. Wtedy kąta theta i psi mamy dane wzorem (37.15). W naszym przypadku dostajemy:
cos theta = (√3)/2 sech (√(5/6) t) = (√3)/ (2 cosh (√(5/6) t) )
theta = arc cos (√3)/2 sech (√(5/6) t) = (√3)/ (2 cosh (√(5/6) t) )
Dla psi, według podręcznika:
tg psi = (1/2) csch (√(5/6) t) = 1/(2 sinhh (√(5/6) t) )
To jest jednak niedobrze. Tak robić nie należy. W pobliżu t=0, gdzie następuje fikołek, tg psi robi się nieskończony, nie wiadomo co wtedy robić. Po zbadaniu sprawy stwierdziłem, że lepiej wziąć to drugie równanie w (37.13) i wyliczyć stąd
cos psi = I2 Ω2(t) / sin theta
psi = arc cos I2 Ω2(t) / sin theta
Pozostaje nam kąt phi. Co piszą Landau i Lifszyc?

Z formuły (37.16) widać, że trzeba obliczyć całkę. Prawa strona (37.16) w naszym przypadku jest łatwa do wyliczenia. Otrzymujemy:
d phi/dt = (√10 cosh √(10/3)t)/( 2 cosh (√(10/3)t) – 1 )
To się daje wycałkować:
phi = (√10) t/2 + arc tan ( √3 tanh (√(5/6) t) )
Teraz jesteśmy w domu. Mamy zależność kątów Eulera od czasu. Możemy pokazać animację fikajacej nakrętki. Tutaj dla t od -20 do 20 co 1/4. Pamiętajmy, że zachowany kręt ustawiliśmy pionowo, zatem fik będzie w pionie a nie w poziomie jak to było na filmie u Dżanibekowa.
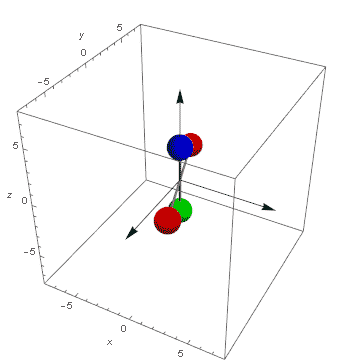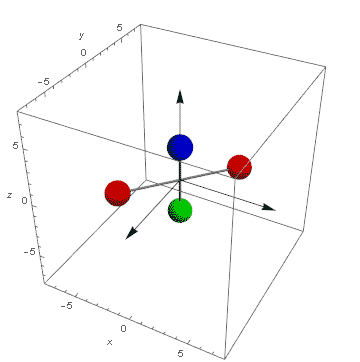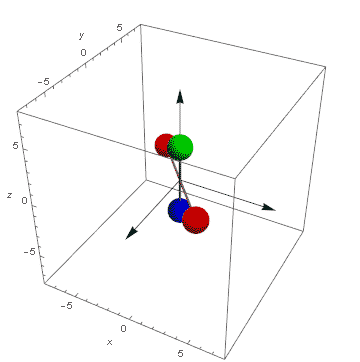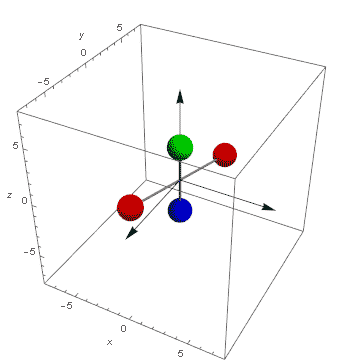
Wyglada to jakoś mało przekonująco z tymi kręcącymi się kulami. Popatrzmy na to samo w innym, bardziej trafiającym do wyobraźni wydaniu:
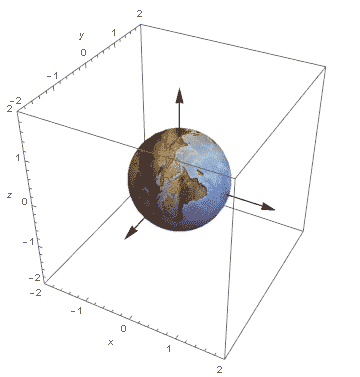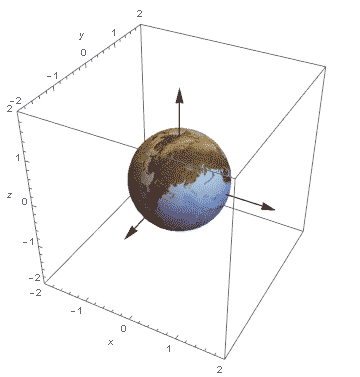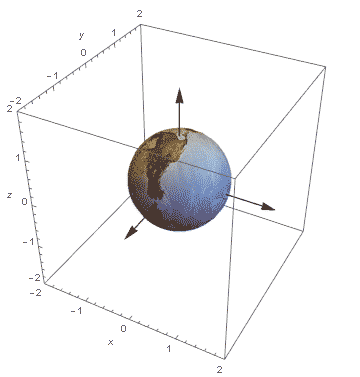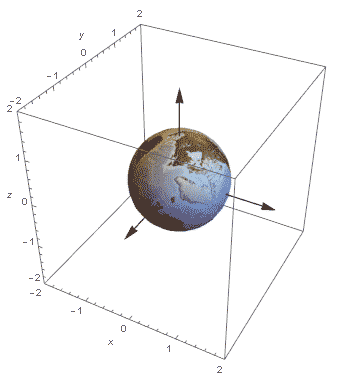
Animacja leci w kółko, więc fikołki się powtarzają, jednak w samej rzeczy jest tylko jeden fikołek, bez reinkarnacji.







Komentarze
Pokaż komentarze (242)