Sinus zdeformowany

Sinusy i kosinusy w szkole dzieci straszą. Ale też, dla wybrednych, to poezja

Matematyka ? królowa, nauka
Jest postrachem każdego nieuka.
Straszy człowieka sinus, cosinus,
Męczy w równaniach każdziutki minus.

     Na klasówkach przed oczami gwiazdki?
     Nie, to tylko koszmarne pierwiastki.
     Kiedy bawisz się w funkcje
     Boisz się, że głowie grożą punkcje.

Szósty raz rozwiązujesz równanie
I czujesz jak twe ciało ogarnia drganie.
A geometria i logika
To dopiero jest gimnastyka.

     Lecz kiedy wreszcie pojmiesz zasady
     Matematyczne triki i rady,
     Każde zadanie staje się proste,
     Wszystko układa się w trele miłosne.

I wtedy rozumiesz, staje się jasne
- twoje myślenie nie jest już ciasne,
Widzisz to wyraźnie jak na neonie
MATEMATYKA siedzi na tronie!!!

Tomasz Regulski, Daniel Dominiak

Grafomani! Siedzi na tronie! Jakim tam tronie? Siedzi na ogonie. Jak kot puszaty.

No właśnie. Mam objaśnić eliptyczny sinus Jacobiego. Co to to takiego? To taki sinus ze szkoły, tyle, że zdeformowany. Takie coś pomiędzy sinusem trygonometrycznym a sinusem hiperbolicznym, ni to ni o wo, ni pies ni wydra. Ale bardzo potrzebne.

Deformacja to ważne pojęcie. Najpierw były okręgi. Te są doskonałe, Potem przyszły elipsy. To zdefoemowane okręgi. A jednak, wbrew bałamucącym ludzi teologom i filozofom, orbity planet bardziej przypominają elipsy niż okręgi. Orbity planet Bóg przecież narysował, jak mogą być niedoskonałe? A jednak są. Z tymi deformacjami to cała historia.

Najpierw była fizyka Galileusza i Newtona, potem (do dziś zresztą) nastąpiła fizyka Einsteina. W fizyce szczególnej teorii względności Einsteina światło rozchodzi się ze skończoną prędkością c. U Newtona i Galileusza z nieskończoną prędkością. Transformacje Galileusza, gdzie c nie występuje są piękne i proste, wręcz doskonałe. Transformacje Lorentza szczególnej teorii względności, gdzie c występuje, są pokićkane. Fizykę Newtona i Galileusza otrzymujemy w granicy gdy c dąży do nieskończoności. Fizykę Einsteina otrzymujemy deformując fizykę Galileusza i Newtona, wprowadzając parametr deformacji c. Deformacja prowadzi do postępu. To tak jak przejście od okręgów do elips.

Podobnie z mechaniką kwantową. Fizykę klasyczną otrzymujemy z fizyki kwantowej przechodząć z wartością stałej Plancka h do zera. Fizykę kwantową otrzymujemy z fizyki klasycznej przez deformację, wprowadzając parametr deformacji h. Ogólnie uważa się, że fizyka kwantowa jest prawdziwsza niż ta klasyczna, że kwantowanie, zatem deformowanie, to postęp.

W ostatnich dziesięciolęciach w fizyce teoretycznej wręcz pojawiła się moda na deformowanie wszystkiego co wpadnie w rękę. Deformowane są więc wszystkie możliwe symetrie i struktury. Jak ktoś coś nowego zdeformuje ma awans gwarantowany, granty zapewnione, wyżywi nie tylko siebie ale i rodzinę, i jeszcze na wczasy zarobi. Tyle, że konkurencja jest spora.

Ale to wszystko na boku. Nas interesuje fikająca nakrętka Dżanibekowa, równania Eulera asymetrycznego bąka i ich rozwiązanie. No i wychodzą zdeformowane sinusy. Nie tylko w niej, ale także w prawdziwym fizycznym wahadle. Sinusy i cosinusy ze szkoły nadają się do uproszczonej rzeczywistości. W rzeczywistości rzeczywistej musimy sinusa zdeformować, okrąg zastąpić elipsą, pocałkować i poróżniczkować. Taka już ona, ta rzeczywista rzeczywistość jest. Czy chcemy czy nie chcemy. Zabieram się więc do roboty. Będą całki i pochodne. Koniec wakacji.

Będę tu korzystał z artykuliku W. Schwalma z Univ. N. Dakota p.t. „Elliptic Functions sn, cn,dn, as Trigonometry”. Wracamy do elipsy z poprzedniej notki. Tyle, że ją „znormalizujemy”. Okrąg ma jeden promień, powiedzmy r. Elipsa ma dwie półosie a,b. Okrąg normalizujemy przyjmując, że r=1. W elipsie nie możemy naraz przyjąć, że a=1 i b=1, bo przestanie być elipsą. Założymy więc, że b=1. Taka będzie nasza normalizacja. Teraz równanie elipsy ma postać:

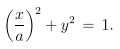
W dalszym ciągu będziemy się posługiwać rysunkiem poniżej:

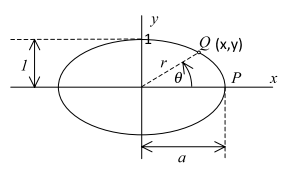
Gdy a=1 wtedy mamy okrąg. Będziemy zakładać, jak na rysunku, że a>1. Innymi słowy znormalizowaliśmy mniejszą oś elipsy. Pozwalamy natomiast jej się rozciągać. Stopień rozciągnięcia elipsy mierzy się jej „ekscentrycznością” czy mimośrodem. W naszym przypadku jest to parametr k dany wzorem

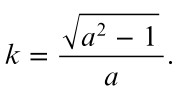
A teraz co nas interesuje? Interesuje nas co się dzieje gdy punkt P porusza się po elipsie. Interesuje nasz punkt Q o współrzędnych (x,y). Dokładniej: interesuje nas współrzędna y. To jest właśnie nasz eliptyczny sinus.

Przypuśćmy, że a=1, czyli, że mamy okrąg (zatem k=0). Wtedy r = 1. Wtedy y = sin(theta). Gdy a>1, sytuacja się komplikuje, deformuje, y nie jest sinusem theta, jest sinusem eliptycznym sn. Tylko czego? I tu się sprawa komplikuje. Musimy wprowadzić dodatkowy parametr, nazwiemy go u, zdefiniowany jako:

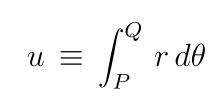
Otóż nasz y to jest sn(u). By zaznaczyć, że idzie o elipsę o mimośrodzie k, piszemy

y = sn(u,k)

Czasami używa się notacji

y = sn(u,m)

gdzie

m = k² = 1-1/a².

To może być mylące, trzeba się domyślać z kontekstu lub wracać do definicji. Różni autorzy używają różnych konwencji. Takie już jest życie. Ja będę używał konwencji sn(y,m), bowiem takiej konwencji używa program komputerowy Mathematica i i takiej konwencji używa encyklopedia Abramowitz, Stegun: Handbook of Mathematical Functions, a ja z nich często korzystam.

Gdy a=1, k=0, r=1, wtedy u=theta. Gdy a > 1, wtedy u to jest u, niby wiadomo co to jest, bo wiadomo co to jest całka, ale żeby to było proste, intuicyjne, by miało jakąś interpretację – tego niestety nie ma. Przynajmniej ja nie znam sposobu jak to u udomowić. Ktoś pewnie kiedyś taki sposób znajdzie. Póki co musimy jednak poprzestać na tym, że wiemy co to jest to u formalnie. I to nam dla naszych celów wystarczy.

Wysokość y widoczna na rysunku jest związana z całką którą oznaczyliśmy przez u. Gdy u rośnie, gdy idziemy powoli od P do Q, wtedy i y rośnie. To znaczy najpierw rośnie a potem, po przejściu poza pionową oś symetrii elipsy, zaczyna maleć.

Zajmijmy się tą pierwszą ćwiartką, kiedy gdy u rośnie, to y też rośnie. Tutaj y jest funkcją od u, ale możemy interpretować też na odwrót, że u jest funkcją od y. A jaką konkretnie funkcją – to postaramy się wyliczyć. Aby to zrobić całkę definiującą u musimy zamienić z całki po kącie w całkę po y. By to zrobić trzeba trochę popracować, ale nie za wiele.

Z obrazka widzimy, że tan θ = y/x. Czyli θ = arc tan y/x. Z równania elipsy x możemy wyrazić przez y. Dla pierwszej ćwiartki

x = a√(1-y²)

Zatem

θ = arc tan (y/(a√(1-y²)))

By zamienić naszą całkę z całki po θ na całkę po y musimy obliczyć dθ /dy.

W wieku komputerów i internetu nie musimy tego robić ręcznie. Idziemy http://www.wolframalpha.com/input/?i=d/dy(arctan(y/(a*sqrt(1-y^2)))

Wpisujemy tam d/dy(arctan(y/(a*sqrt(1-y^2))) i dostajemy odpowiedź

 

Zauważmy, że (y²-a²(y²-1))=(y²+a²(1-y²))=y²+x² = r².

Teraz

du/dy = du/dθ dθ /dy

du/dθ znamy, to r. Stąd wychodzi

du/dy = 1/√((1-y²)(1-my²)).

Ale pochodna funkcji odwrotnej to odwrotność pochodnej funkcji, zatem

dy/du = √((1-y²)(1-my²))

Widzimy więc, że nasza funkcja y = sn(u,m) spełnia nieliniowe równanie

(dy/du)² = (1-y²)(1-my²)

Możemy to porównać z tym co mamy w Wikipedii

 

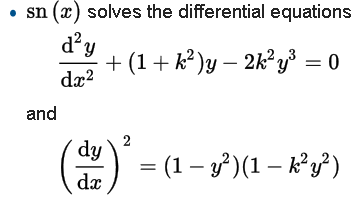
To samo, tylko zapisane trochę inaczej.

Napociliśmy się trochę, ale widzimy, że funkcję eliptyczną Jacobiego sn da się ugryźć bez łamania na niej zębów. W następnej notce jeszcze ją trochę pożujemy zanim pójdziemy dalej naszą drogą.