Co jest lepsze? Postęp czy kręcenie się w kółko? Ruch jednostajny postępowy jest doprawdy nudny. W jadącym pociągu spać się chce. Jak mówi poeta:
Do taktu turkoce i puka, i stuka to:
Tak to to, tak to to , tak to to, tak to to.
Gładko tak, lekko tak toczy się w dal,
Jak gdyby to była piłeczka, nie stal
Nic doprawdy ciekawego. Po prostu inny układ inercjalny. No, może eter wiaterkiem podmucha, ale to wszystko. Co innego wirujący jednostajnie dysk.
 Karuzela
Karuzela
Też jednostajnie, ale wiruje a nie postępuje. To zupełnie co innego. Świat się kręci, kręci się w głowie, zmienia się geometria, czai się tam na nas paradoks Ehrenfesta.
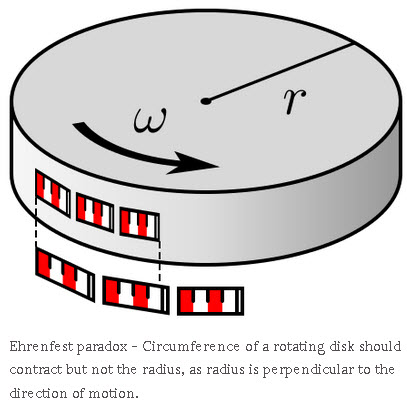
Mamy też ułatwione przejście do innych stanów świadomości a może i do innej rzeczywistości

Wirujący derwisze Rumi
Ruch wirowy to groźna do oswojenia bestia. My zaczęliśmy od oswajania swobodnie wirującego w przestrzeni niesymetrycznego bąka, co to fikołki może fikać, bez widocznego powodu jak ta nakrętka w kosmosie u Dzhanibekova. Już rok bodaj mija odkąd to zjawisko wpadło mi w oko i zaciąłem się, że naprawdę do głębi po swojemu zrozumiem. I ciągnę tę serię notek jak głupi, dzieląc się tym co udało mi się już zrozumieć. Jest to bardziej działalność artystyczna niż naukowa, bowiem mało kto tym się naprawdę zajmuje. No, chyba, że specjaliści od sterowania statkami kosmicznymi, ale tych nie ma znów aż tak wielu, zaś od zapobiegania fikołkom mają małe chytre silniczki.
By bąka, nakrętkę fikająca w kosmosie, oswoić, trzeba poznać język ideogramów używany przez Przyrodę, w naszym przypadku funkcje eliptyczne Jacobiego sn, cn, dn. W poprzedniej notce oswoiliśmy nieco zdeformowany sinus, funkcję cn(u,m). Pozostała nam jeszcze funkcja dn(u,m) – ta będzie zdeformowaną funkcją stałą, zdeformowaną jedynką. Ta notka jest kontynuacją notki poprzedniej i nie będę drugi raz tego co tam było powtarzał. Przypomnę tylko podstawowe formułki, ale teraz już bez wyjaśniania.
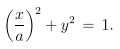
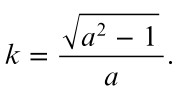
m = k2 = (a2-1)/a2= 1 – 1/a2
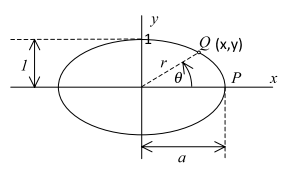
x(θ) = r(θ) cos θ
y(θ) = r(θ) sin θ
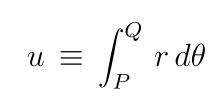
Funkcję dn(u,m) jako
dn(u,m) = z = r/a
Zauważmy, że dla a=1, gdy elipsa staje się okręgiem, r = 1, u=θ, m=0. Zatem dn(u,0) = 1.
Funkcja dn(u,m) dla m większych od zera i mniejszych lub równych 1, to zdeformowana funkcja stała i równa tożsamościowo 1. A co w międzyczasie? Podobnie jak to było z sn i cn znajdźmy równanie spełniane przez funkcję dn. Z równania elipsy znajdujemy
z2 cos2θ + z2a2sin2 θ =1
Stąd
θ = arc sin (√ ( (1-z2) / (a2-1) ) / z )
i dalej już jak poprzednio dochodzimy, po małych i prostych rachuneczkach, do
(dz/du)2 = (1-z2) (z2+ m -1)
Co porównujemy z tym co znajdujemy Wikipedii (drugie równanie)
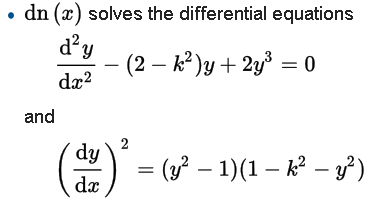
Zgadza się. Zauważmy, że dla u=0 winniśmy mieć z= 1. Gdy m=0 (czyli dla okręgu) mamy równanie
(dz/du)2 = (1-z2)(z2-1)
i z2 równe tożsamościowo jeden je spełnia. A co na drugim końcu? Gdy elipsy staje się nieskończenie rozciągnięta, gdy m=1?
Gdy m=1 dostajemy
dz/du = z√ (1-z2)
dz/( z√ (1-z2) ) = du
Stąd, po scałkowaniu
u =log ( z/(1+√ (1-z2) ) )
I możemy stąd znaleźć z jako funkcję u
dn (u,1) = z = 1/cosh u
Wykres tej funkcji ma postać:
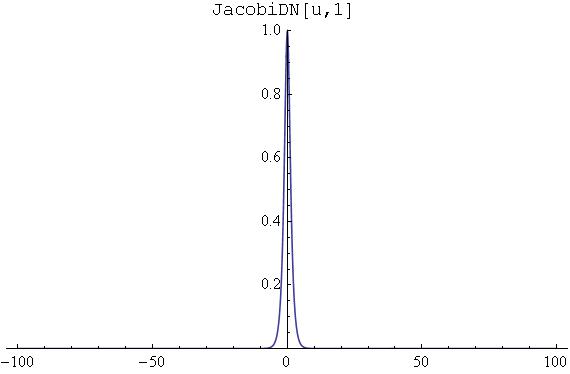
Dla m bliskiego jedynki, m=0.999999, wykres funkcji dn(u,0.999999) ma postać
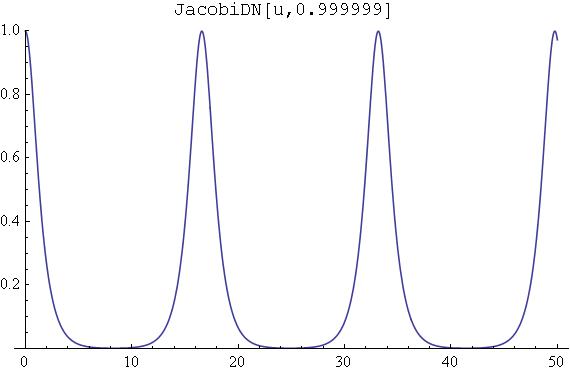
Co pół okresu następuje fikołek. W miarę jak m zbliża się do 1, fikołki stają się coraz rzadsze. W granicy m=1 jest tylko jeden fikoł, w pobliżu t=0.
Oczywiście o tych fikołach mówię na wyrost, bowiem na razie mamy jedynie trzy funkcje eliptyczne sn, cn, dn (uogólnienie sinusa, cosinusa i jedynki) i nie wiemy jeszcze co one do fikania mają. Z rozwianiem tej tajemnicy musimy wszakże poczekać do następnej notki, a może i do następnej następnej.







Komentarze
Pokaż komentarze (12)