Euler rozszyfrowany

Znacie tę zagadkę? W każdym rogu pokoju (standardowego, czworokątnego) siedzi jeden kot. Naprzeciwko każdego kota siedzi jeden kot. Na ogonie każdego kota siedzi jeden kot. Ile jest kotów w pokoju?

To stara zagadka. Nowa, ambitniejsza zagadka jest taka:

Wektor krętu ma trzy składowe. Szybkość zmiany każdej ze składowych jest proporcjonalna do iloczynu dwóch pozostałych. Jak się zmieniają w czasie te składowe?

To właśnie jest sprawą rozwiązania równań Eulera dla swobodnego asymetrycznego bąka. Było o tym w poprzedniej notce Nawrócenie Jacobiego:

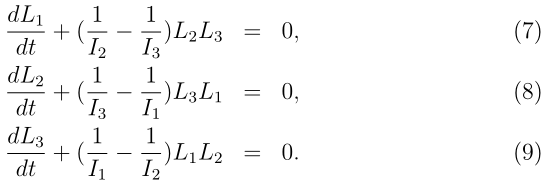
Od razu chciałoby się pomyśleć jak by takie równania wyglądały w czterech wymiarach, jak to było z kotami w czterech rogach. Czy prędkość zmiany każdej składowej byłaby proporcjonalna do iloczynu trzech pozostałych? Jednak z uogólnieniami trzeba być ostrożnym. Bowiem kręt, z natury rzeczy, jest biwektorem a nie wektorem. I tylko w trzech wymiarach wektory i biwektory dają się utożsamić. W innych wymiarach ta sztuczka nie działa. Tak więc z uogólnianiem równań swobodnego bąka na cztery wymiary nie należy się śpieszyć. Zróbmy lepiej do końca przypadek trzech wymiarów.

Napisałem w poprzedniej notce, że znaleźć rozwiązanie równań Eulera przy pomocy funkcji eliptycznych Jacobiego jest prosto. W samej rzeczy rozwiązanie ma postać

L₁(t) = A1cn( B t,m)

L₂(t) = A2 sn (B t,m)

L₃(t) = A3 dn (B t,m)

gdzie A1,A2,A3,B oraz m to stałe. Trzeba tylko te stałe odpowiednio dobrać. A jak je dobierać? Tu jest trochę roboty. Nie będę tej żmudnej algebraicznej roboty tu robił. Można to zlecić komputerowi, można zlecić studentowi. Podam jedynie wynik i pokażę jak wynik sprawdziłem.

Najpierw jednak, by wzory, których będziemy używać trochę odkomplikować zrobimy jedną umowę. Wiemy, że kwadrat długości krętu jest stały w czasie:

L₁²+L₂²+L₃²= L² = const.

Przypomnijmy, że składowe L1,L2,L3 są proporcjonalne do odpowiednich omeg, do składowych prędkości kątowej. Możemy tak w danym zagadnieniu dobrać jednostkę czasu, by długość wektora krętu wynosiła 1:

L² = 1.

Zatem będziemy zakładać, że wektor krętu L ma długość 1, leży na powierzchni jednostkowej sfery i tam jakoś, zgodnie z równaniami 7-9 wraz czasem się zmienia.

By określić stałe A1,A2,A3,B potrzebna nam są momenty bezwładności I1,I2,I3 oraz stosunek podwojonej energii kinetycznej do L². Oznaczymy go symbolem d = 2Ek/L² . Skoro przyjęliśmy L² = 1, zatem d = 2Ek. Dla porządku umówimy się też, by osie układu wirującego wraz z bąkiem ponumerować tak, by było

I1 < I2 <I3

Przy tych umowach możemy otrzymać rozwiązanie równań (7),(8),(9) powyżej kładąc:

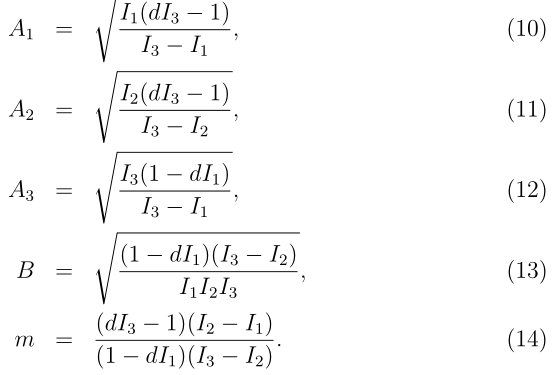
Tak jest gdy d>1/I2. Bowiem gdy d<1/I2, wtedy trzeba w tych formułach I1 i I3 zamienić miejscami. Zaś gdy d=1/I2, wtedy m=1 te formuły można zapisać prościej, o czym osobno porozmawiamy.

Najpierw, nawet przed sprawdzaniem i przed stosowaniem do prawdziwych bąków, trzeba będzie się tym formułom przyjrzeć, czy w ogóle mają sens?

Mamy pierwiastki kwadratowe. Pod tymi pierwiastkami, jak się im przyjrzeć, zobaczymy znaki minus. Danger! Danger! To co jest pod pierwiastkiem lepiej nich będzie dodatnie, przynajmniej nieujemne. Inaczej wylądujemy w urojonym świecie, i to bez biletu powrotnego. Jest więc co robić. Jest praca. To dobrze. Praca wyzwala.