https://www.nature.com/news/history-einstein-was-no-lone-genius-1.18793Tekst poniżej jest długim cytatem ze strony 142 książki Krzysztofa Maurina "Matematyka i fizyka". Wklejam bez zmian, urozmaicając jedynie obrazkami. W tekście tym mowa o roli Riemanna. Polskie tłumaczenie wykładu habilitacyjnego Riemanna "O hipotezach, które leżą u podstaw geometrii", o którym mowa w tekście jest dostępne tutaj. Więcej o Riemannie i jego trudnym życiu w książce M. Kaku "Hiperprzestrzeń". Co do faktycznych Riemanna w rozwoju "nowej geometrii" - są tu kontrowersje. Warto zajrzeć więc do artykułu Scholza "Riemann's vision of a new approach to geometry" i do artykułu Portnoya "Riemann's contribution to differential geometry". A oto tekst str. 142 z książki Maurina "Matematyka a fizyka" - książka bardzo trudno dostępna, ale warta zdobycia!
https://ksiegarnia.pwn.pl/Matematyka-a-fizyka,68454875,p.html
Krzysztof Maurin, "Matematyka a fizyka", str. 142:
Najgłębsze rozważania, zarówno za, jak i przeciw wielkiej teorii naukowej pojawiaj ą się zaraz po jej powstaniu (tak było np. z darwinizmem: najgłębszą jego krytykę podał wielki filozof E. von Hartmann).
Stopień refleksji nad teorią kwantów i nad teorią względności Einsteina był nieporównanie wyższy w latach dwudziestych niż obecnie, dlalego w tym co niżej będę czerpał z prac i książek H. Weyla.
Jak już pisałem, przełomowym wydarzeniem w teorii przestrzeni był wykład habilitacyjny Riemanna Über die Hypothesen, welche der Geometrie zu Grunde liegen (1854). Riemann dopuszczał możliwość, że przestrzeń fizyczna nie jest euklidesowa. Dopuszczał nawet, że może mieć strukturę dyskretną. W genialnej wizji Riemann twierdził, że struktura metryczna przestrzeni (tensor metryczny o składowych (gik)) jest zmienna, że prrestrreń nie jest jednorodna, co więcej, że pole (gik) zależy od rozkładu materii w przestrzeni. Była to śmiałość niewiarygodna i z odzewem spotkała się jedynie u Clifforda.
Fizykalna koncepcja Riemanna popadła w zapomnienie - tym intensywniej rozwijano aspekty analityczne i geometryczno -różniczkowe (Christoffel i szkoła włoska wokół Ricciego).
Przyszedł rok 1905, rok, w którym Einstein napisał trzy przełomowe pmce! Nas interesuje tutaj jedynie praca zawierająca ,,szczególną teorię względności ". Można powiedzieć, że koncepcja tej pracy wisiała w powietrzu: pojawiły się już pace H. Lorentza i H. Poincarégo (który zauważył grupowość przekształceń Lorentza).
Henri Poincaré
Koncepcję Einsteina podjął natychmiast H. Minkowski - wielki geometra i arytmetyk (przyjaciel Hurwitza i Hilberta),
History: Einstein was no lone genius
Einstein, mówiąc nawiasem, był "uczniem" Minkowskiego na Eidgossische Technische Hochschule (politechnika w Zurychu, duma Szwajcarii, miała zawsze świetnych matematyków - byli to przeważnie genialni młodzi docenci z Niemiec!).
ETH Zurych
Einstein nie uczęszczał systematycznie na wykłady Minkowskiego: uczył się ze świetnie prowadzonych notatek swego przyjaciela, matematyka Grossmanna. Od 1905 r. Minkowski miał systematyczne wykłady z elektrodynamiki ciał w ruchu i w istotny sposób wzbogacił teorię Maxwella.
Hermann Minkowski
W latach 1907-1908 Minkowski wyjaśnił geometryczny sens szczególnej teorii względności, wprowadzając czterowymiarową przestrzeń wektorową R4, wyposażoną w formę kwadratową
Q(x) = x02-x12-x22-x32.
Przekształcenia Lorentza to automorfizmy przestrzeni (R4, Q), a więc przekształcenia
liniowe g z GL(R4), zachowujące formę Q:
Q(gx) = Q(x), x należy do R4
Punkt x należący do M4 = (R4, Q) nazywa się zdarzeniem. Istotną rolę odgrywa stożek Q(x) = O, tzw. stożek świetlny. (Jego tworzące odpowiadają promieniom świetlnym przechodzącym przez punkt 0 w M4 .)
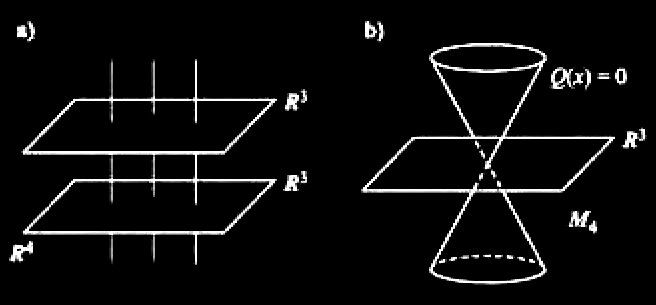
Rysunek a przedstawia czasoprzestrzeń Newtona (w której czas jest wielkością bezwzględną, absolutną); rysunek b przedstawia czasoprzestrzeń Minkowskiego. W geometrii Minkowskiego sygnały świetlne są najszybszymi sygnałami , światło rozchodzi się ze skończoną prędkością (naturalna jednostka prędkości).
