Koronawirus krązy po świecie, krąży. Puka do drzwi, okien, na spotkanie zaprasza. Tak trudny czas skłania do zrobienia czegoś co wydawało się niemożliwe a tym czymś jest tytułowe zderzenie. A to wskazuje coś z Nauki.
Mamy tu dwie równości wynikające z odpowiednich praw zachowania: suma energii przed zderzeniem jest równa sumie energii po zderzeniu oraz suma pędów przed zderzeniem jest równa sumie pędów po zderzeniu.
Zderzenie dwóch ciał liczy się na fizyce w szkole średniej. Dla zadanych 2 mas i ich 2 prędkości przed zderzeniem wyliczamy 2 prędkości po zderzeniu. Mamy 2 równania 2 niewiadome, nieskomplikowane wzory i licealiści powinni to umieć rozwiązać. W Wikipedii takie rozwiązanie jest podane.
https://pl.wikipedia.org/wiki/Zderzenie_spr%C4%99%C5%BCyste
A dla większej liczby ciał mamy dalej 2 równania ale N niewiadomych. Wydaje się, że rozwiązanie jest niemożliwe, ale czy na pewno przecież przyroda jakoś sobie z tym musi radzić, zderzano tryliony cząstek i nie zauważono zawahania się jak mają one lecieć po zderzeniu. Więc muszą być jakieś dodatkowe ukryte związki, które nie są natychmiast widoczne, tak jak w zagadce.
Zagadka, którą kiedyś usłyszałem (co wypomniał mi Karlus).
Spotkało się dwóch matematyków po wielu latach, opowiadają o sobie o dzieciach i jeden z nich odpowiada zagadkowo
Mam 3 dzieci, iloczyn ich lat wynosi 36 a suma lat tyle ile okien w domu naprzeciwko. Drugi liczy i mówi to nie jest jednoznaczne, potrzebuję jeszcze dodatkowej informacji. Pierwszy dodaje – najstarsze na zeza. Świetnie, odpowiada drugi – mają one … lat, … lat i … lat.
Ile - podam dalej, bo może ktoś samodzielnie zechce rozwiązać.
Do analizy zderzeń wezmę teorię względności, a w szczególności pomocną RAPIDITY.
https://en.wikipedia.org/wiki/Rapidity
Jest to odpowiednia bezwymiarowa parametryzacja prędkości v bardzo ułatwiająca obliczenia. Zdefiniowana jest przez funkcję tangens hiperboliczny.
v/c=tanh(V), c jest prędkością światła.

Ponieważ będzie wiele prędkości więc te przed zderzeniem oznaczę przez uk, po zderzeniu vk. Odpowiadające im rapidity oznaczę dużymi literami Uk i Vk.
Co ułatwia rapidity:
1. Dla dowolnego V wyliczona prędkość v nie wykracza poza przedział ograniczony prędkością światła (–c, c).
2. Transformacja Lorentza jest zastąpiona obrotami hiperbolicznymi.
3. Relatywistyczne dodawanie prędkości jest zastąpione przez zwykłe dodawanie odpowiadających rapidity.
4. Energia ciała wyraża się następująco E=m*c2*cosh(V), natomiast pęd p= m*c*sinh(V).
5. I jeszcze trochę innych.
Widać, że należy zajrzeć do funkcji hiperbolicznych. Dla przykładu z definicji funkcji tanh mamy
u/c=tanh(U)=(eU-e-U)/(eU+e-U), a stąd możemy wyliczyć eU=((c+u)/(c-u))1/2. Czyli słowami liczba e podniesiona do potęgi rapidity U jest pierwiastkiem z wyrażenia z prędkościami (c+u)/(c-u).
Podpowiedź do zagadki - drugi matematyk wie ile jest okien. To ważne.
Równania opisujące zderzenia sprężyste N mas m1, m2,…,mN przyjmują postać, energetyczne
m1*c2*cosh(V1)+ m2*c2*cosh(V2)+…+ mN*c2*cosh(VN)=
=m1*c2*cosh(U1)+ m2*c2*cosh(U2)+…+ mN*c2*cosh(UN)
pędowe
m1*c*sinh(V1)+ m2*c*sinh(V2)+…+ mN*c*sinh(VN)=
=m1*c*sinh(U1)+ m2*c*sinh(U2)+…+ mN*c*sinh(UN)
Wygodniej będzie przedstawiać w postaci wykładniczej. Korzystam ze związków cosh(X)+sinh(X)=eX oraz cosh(X)-sinh(X)=e-X. Raz dodając stronami równania energetyczne i pędowe, po wcześniejszym podzieleniu przez odpowiednią potęgę c, drugi raz odejmując. Otrzymujemy
(A)....m1*eV1+ m2*eV2+…+ mN*eVN= m1*eU1+ m2*eU2+…+ mN*eUN
(B)....m1*e-V1+ m2*e-V2+…+ mN*e-VN= m1*e-U1+ m2*e-U2+…+ mN*e-UN
Równość stron równań jest zachowana gdy wykonamy nad tymi stronami takie same działania.
(m1*eV1+ m2*eV2+…+ mN*eVN)*( m1*e-V1+ m2*e-V2+…+ mN*e-VN)=
=( m1*eU1+ m2*eU2+…+ mN*eUN)*( m1*e-U1+ m2*e-U2+…+ mN*e-UN)
Po rozpisaniu otrzymamy równość wielomianów iloczynów mas mk*ml ze współczynnikami, którymi po redukcji będą kosinusy hiperboliczne. Rozpiszę je w sposób jawny dla N=3.
mk*ml…...............rapidity V....................rapidity U
m1*m1…...............1......................................1
m1*m2…...............2*cosh(V1-V2)....................2*cosh(U1-U2)
m1*m3…...............2*cosh(V1-V3)....................2*cosh(U1-U3)
m2*m2…...............1......................................1
m2*m3…...............2*cosh(V2-V3)....................2*cosh(U2-U3)
m3*m3…...............1......................................1
Ponieważ równość ma byś spełniona dla dowolnych (niezerowych) mas więc odpowiednie kosinusy hiperboliczne muszą być równe.
Podpowiedź do zagadki - drugi matematyk też rozpisał wszystkie iloczyny lat.
Iloczyn........Suma
36=36*1*1.....38
36=18*2*1......21
36=12*3*1.......16
36=9*2*2..........13
36=9*4*1.........14
36=6*3*2..........11
36=6*6*1.........13
Zagadnienie zderzenia jest spełnione gdy wszystkie kosinusy są sobie równe. To zagadnienie musi mieć rozwiązanie trywialne czyli ciała mijają się i lecą bez zmian. To jest spełnione gdy
V1-V2=U1-U2 i V1-V3=U1-U3. Dla dowolnej liczby N kontynuujemy aż do V1-VN=U1-UN. Pozostałe równości są zależne.
Ponieważ wtedy, po podstawieniu, wszystkie rapidity V są równe rapidity U a tym samym wszystkie prędkości v są równe prędkościom u.
Jest wiadome, że funkcja cosh jest symetryczna, czyli cosh(X)=cosh(-X). Oznacza to, że możemy zmienić znaki bez zmiany wartości funkcji cosh. I to jest drugie rozwiązanie zagadnienia.
V1-V2=-U1+U2 i V1-V3=-U1+U3. Wyliczam rapidity V2=V1+U1-U2 i V3=V1+U1-U3. I podstawiam do równania (A) oczywiście skróconego do sumy 3 składników.
m1*eV1+ m2*eV1+U1-U2+m3*eV1+U1-U3= m1*eU1+ m2*eU2+m3*eU3
Mamy tu tylko jedną niewiadomą V1, którą rozwiązujemy. Otrzymujemy
(C)...eV1= (m1*eU1+ m2*eU2+m3*eU3)/(m1+ m2*eU1-U2+m3*eU1-U3)
Następnie wyliczamy do podstawienia raz V1=V2-U1+U2 i podstawiając pod powyższe otrzymamy
(D)...eV2= (m1*eU1+ m2*eU2+m3*eU3)/(m1*eU2-U1+ m2+m3*eU2-U3)
drugi raz V1=V3-U1+U3 i znów podstawiając otrzymamy
(E)...eV3= (m1*eU1+ m2*eU2+m3*eU3)/(m1*eU3-U1+ m2*eU3-U2+m3).
Można dostrzec regularność, podam ją dla N ciał
(F)...eV1+U1= eV2+U2=...=eVN+UN=(m1*eU1+ m2*eU2+..+mN*eUN)/(m1*e-U1+ m2*e-U2+mN*e-UN).
Widzimy, że ze względu na różnowartościowość funkcji wykładniczej sumy rapidity przed zderzeniem i po zderzeniu są takie same dla każdego ciała uczestniczącego we wspólnym zderzeniu.
Podpowiedź do zagadki, bardzo ważna - drugi matematyk miał wątpliwość, ta informacja praktycznie daje rozwiązanie.
Można wartości rapidity przeliczyć na prędkości, dla przykładu równanie (C) po drobnym szlifie przyjmie postać
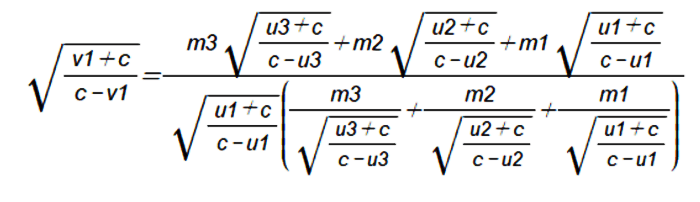
Można z tego wyliczyć prędkość v1 w zależności od innych prędkości, ale wyrażenie jest zbyt długie by je przepisywać. Można dla małych prędkości, w porównaniu z prędkością światła, przybliżyć przez rozwinięcie w szereg Taylora, urywając na wielomianie 1 stopnia od wszystkich prędkości u.
Rachunki są długie ale wynik krótki. Po zebraniu w całość z innymi równaniami z v2, v3,...,vN mamy odpowiednik równania (F) dla małych prędkości
(G)...v1+u1=v2+u2=...=vn+un=2*(m1*u1+m2*u2+...+mN*uN)/(m1+m2+...+mN).
Słowami można to wyrazić tak.
Suma prędkości przed zderzeniem i po zderzeniu każdego ciała jest równa dwa razy uśrednione po masach prędkości przed zderzeniem wszystkich ciał uczestniczących w zderzeniu.
I to co było niemożliwe stało się łatwe. Krytyczną własnością umożliwiającą rozwiązanie jest symetria funkcji kosinus hiperboliczny wynikająca ze skorzystania z uprzejmości rapidity. Ciekawe czy pomysłodawcy wprowadzenia tej parametryzacji przewidzieli i to co jest w tej notce.
Uzupełnienie.
Jeżeli jakaś para (lub więcej niż para) ma te same prędkości uk lub takie same rapidity Uk oraz zderzają się w tej samej chwili i w tym samym puncie to oznacza, że leciały razem, z równań (F) lub przybliżonych (G) wynika, że będą miały te same prędkości vk lub rapidity Vk, czyli będą dalej leciały razem. Widać to w wahadle Newtona
http://www.deltami.edu.pl/temat/fizyka/mechanika/2016/04/26/Wahadlo_Newtona/
Dodatkowo, jeżeli zderzające się inne masy sa takie same to mogą zgodnie zmienić swoje parametry i jeżeli były w bezruchu to odpowiednia para osiągnie prędkość początkowej pary. W wahadle Newtona rozpędzona para zwróci parametry do początkowej pary.
W przypadku sprężystego zderzania złożonej cząstki (np. z 3 kwarków) z innymi cząstkami taki klaster nie rozpadnie się. A jeżeli będą zderzać się inne klastery to nie będzie również wymiany podskładników. Ale to co w zderzaniu cząstek jest najciekawsze to jednak rozpady i wymiany. Tak więc przydałby się opis zderzeń niesprężystych ale taki bardziej szczegółowy a nie ogólne zachowanie energii i pędu złożonego układu.
Rozwiązanie zagadki.
Spójrzmy na wyliczankę zrobioną przez drugiego matematyka. Jest tylko 1 para równych sum. I tylko w tym przypadku drugi matematyk mógł mieć wątpliwości. Rozstrzygnęła ją odpowiedź, że najstarszy ma zeza a najstarszy jest tylko w przypadku wieków dzieci: 9 lat, 2 lata, 2 lata. Tak więc wszystkie dane do rozwiązania były, wystarczyło je uwzględnić.








Komentarze
Pokaż komentarze (15)