Taki dziwoląg ulągł się w podkomisji w wykonaniu Glenn Joergensena.
W podręcznikach fizyki próżno szukać takiego określenia, a nawet wyraźnie wskazuje się, że energia kinetyczna ciała o masie M i prędkości V=(Vx,Vy,Vz) (ograniczam się do ruchu postępowego i zakładam, że składowe prędkości są prostopadłe do siebie) jest skalarem i wyraża się przez jedną wartość, niezależną od kierunku i równą
Ek = M*V^2/2, gdzie V^2 = Vx^2+Vy^2+Vz^2.
Tak jest w podręcznikach na całym świecie, również w Danii czyli źle się dzieje ale nie w państwie duńskim. Ta informacja jest np. dla tegorocznych maturzystów poprawkowiczów, by nie dali się nabrać autorytetom Podkomisji i nie zawalili poprawki.
Kilka cytatów z wersji polskiej (wytłuszczenia są moje)
https://wnet.fm/kurier/fakty-kontra-fotelowi-eksperci-artymowicz-lasek-czachor-braun-g-p-jorgensen-kurier-wnet-28-201/
i angielskiej (są tam lepszej jakości obrazki)
http://www.smolenskcrashnews.com/smolensk-crash-facts-versus-armchair-experts.html
„Często stosowaną przez tzw. ekspertów metodą dezinformacji jest mieszanie ze sobą prędkości poziomych i pionowych lub kierunków energii. Jest to dowód całkowitej ignorancji, niedopuszczalnej w profesjonalnych badaniach śledczych.”
„Wszyscy trzej – Maciej Lasek, Paweł Artymowicz, Marek Czachor – już wcześniej wspominali, że inny samolot, który rozbił się w podobnych warunkach, uległ rozbiciu na wiele części, i podają przykład lotu Swiss Air 111[viii]. Ten samolot, odwrócony do góry dnem, uderzył w wodę z prędkością 560 km/h, pod kątem 20 stopni. Oznacza to, że prędkość pionowa wynosiła około 190 km/h (niemal pięciokrotnie więcej niż w Smoleńsku), a woda działa przecież jak beton przy takich prędkościach pionowych. W przypadku katastrofy w Smoleńsku prędkość pionowa wynosiła poniżej 43 km/h. Innymi słowy, Swiss Air 111 uderzył z około 20 razy większą pionową energią kinetyczną masy jednostkowej niż w przypadku Smoleńska (190/43)². ”
„Zamiast tego przykładu dezinformacji mógł on pokazać przypadek sprowokowanej w celach testowych katastrofy samolotu siostrzanego do tupolewa, zbudowanego przez Boeinga (727) na twardym, skalistym podłożu pustynnym w Meksyku w 2012 roku[x] (patrz rys. 11). W ostatniej fazie lotu pilot opuścił samolot, który dalej był sterowany zdalnie do ziemi. Ten statek powietrzny uderzył w ziemię z siłą około połowy mniejszej pionowej energii kinetycznej na masę jednostkową w porównaniu z przypadkiem smoleńskim, ale biorąc pod uwagę fakt, że uderzył w twarde podłoże, a nie stosunkowo miękkie, jak to było w Smoleńsku, można założyć, że oba przypadki są dość porównywalne.”
Te cytaty świadczą, ze to nie jest przypadkowa pomyłka. I nie jest ona niezbędna do wyjaśnienia czegokolwiek, a po to by epatować wielkością energii kinetycznej drzwi – 125 m/s prędkość wystrzelenia drzwi zakładaną jako potrzebną do wstrzelenia ich na 1 m w głąb gleby, przy 12 m/s prędkości opadania samolotu (przy prędkości samolotu 75 m/s) co miało by dać (125/10)^2 około 100 razy większą energię, a tym samym konieczność wybuchu.
Skorzystanie natomiast z prawidłowego wzoru daje wzrost zaledwie (125*125+75*75)/(75*75) = 3,77 razy.
Można by rzec, że spatałaszyli sprawę bo np. biorąc przykład przy początkowej prędkości opadania 0 mm/s i końcowej 1 mm/s otrzymalibyśmy według obliczeń podkomisji nieskończony wzrost „pionowej” energii kinetycznej i można byłoby straszyć nie eksplozją nie termobaryczną ale hipertermojądrową.
Odnosząc się do zamieszczonego tam rysunku (co byłoby gorsze)

Przyjmę, że samolot nie jest w przeciągnięciu i leci z prędkością po przeciwprostokątnej 70 m/s. Dodam jeszcze obliczenia dla przypadku normalnego lądowania.
Prawidłowa prędkość opadania dla Tu-154 powinna być 3 m/s. Składowa pozioma wynosi wtedy Vx = pierwiastek(70*70-3*3) m/s = 69,936 m/s. Do wygaszenia składowej pionowej amortyzatory muszą pochłonąć 3*3/(70*70) = 0,001837 części energii całkowitej. Reszta energii jest hamowana na drodze wielu setek metrów. Tak wygląda normalne hamowanie.
Na rysunku łagodny kąt wynosi około 14 stopni, odpowiada temu składowa prędkości pionowej Vy = 70*sin(14) = 17 m/s. Do wygaszenia jest 17*17/(70*70) = 0,059 części energii całkowitej, czyli 32 razy więcej niż w poprzednich obliczeniach. Amortyzatory tego nie wytrzymują i samolot rozpada się. Na drodze m.in. pasażerów wyrasta bariera szczątków. Hamowanie jest katastrofalnie gwałtowne i pasażerowie mogą zginąć w rozpadającym się samolocie. Przy drugiej części Vy = 70*sin(76) = 68 m/s i otrzymujemy katastrofę bardziej gwałtowną. Żadna z obu rysunkowych alternatyw nie prowadzi do przeżycia.
Inną sprawą jest osiągnięcie w wybuchu prędkości 125 m/s. W prostym obliczeniu wyznaczymy jakie maksymalne ciśnienie musiałoby działać na drzwi tupolewa.
Z wzoru na zmianę pędu i impuls siły (popęd) mamy
Masa drzwi * zmiana prędkości drzwi = średnia siła fali uderzeniowej działającej na drzwi * czas działania.
Masa drzwi wynosi około 50 kg, zmiana prędkości drzwi 125 m/s.
Z wykresu ciśnienia fali uderzeniowej
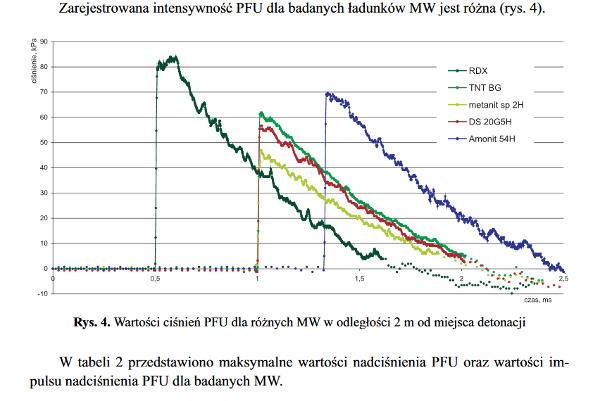
widzimy, że dla wybuchu TNT (zielona krzywa) umieszczonego w odległości 2 m fala uderzeniowa dochodzi czujnika po 1 ms = 0,001 s i ma tam maksymalną wartość Pmax. Tzw. Impuls ciśnienia jest równy polu pod krzywą wykresu i można przybliżyć to pole trójkątem prostokątnym tak dopasowanym, by skośny bok był sumaryczne tyle samo nad wykresem i pod wykresem (wysokość * podstawa / 2). W przybliżeniu linia boku przechodzi przez oś czasu w chwili 2 ms. Czyli czas działania ciśnienia możemy oszacować na 1 ms. Tak więc impuls siły działający na drzwi o wysokości 1,8 m i szerokości 0,8 m wynosi
1,8 m * 0,8 m * Pmax * 0,001 s/2.
Podstawiając otrzymujemy
50 kg * 125 m/s = 1,8 m * 0,8 m * Pmax * 0,001 s/2
Stąd ciśnienie Pmax jest około 10 000 000 paskali czyli 100 atmosfer.
Z danych technicznych Tu-154 wiemy, że nadciśnienie w części hermetycznej nie powinno przekraczać 0,7 atm. Pomnożone przez współczynnik bezpieczeństwa 2 wiemy, że poszycie wytrzymuje do 1,4 atm. To jest wartość 100 razy mniejsza od ciśnienia niezbędnego do wystrzelenia drzwi. Wyjaśnianie przykładem korka od szampana nie ma tu żadnych podstaw. Butelka szampana jest na tyle gruba by wytrzymać ciśnienie potrzebne do wystrzelenia korka. Natomiast wpływ poszycia mieści się w granicach błędu oszacowań, czyli może być pominięty.
Ile trzeba TNT by wytworzyć ciśnienie 140 atm w odległości 1,9 m (środek samolotu). Odpowiedni (półempiryczny) wzór możemy znaleźć w Prawie geologicznym i górniczym Dz.U. 2002, Nr 190, poz. 1589, ma on postać (w atmosferach)
Pmax = 9,8 * (r * G^(-0,33))^(-1,89)
W naszych obliczeniach Pmax = 100 atm, r = 1,9 m, G – masa wzorcowego heksogenu w kg. Dla TNT należy pomnożyć przez 1,3.
Po podstawieniach otrzymujemy masa TNT = 274 kg * 1,3 = 356 kg.
Oznacza to, że w w środku samolotu na przeciw drzwi (wybuchniętych) powinna była stać wielka beczka zawierająca więcej niż 1/3 tony TNT. I nikt jej nie zauważył.








Komentarze
Pokaż komentarze (52)