Kontinuum- eter - foton.
Dostrzegłam pewne nieścisłości w moich wcześniejszych publikacjach. Teraz spróbuję poprzednie błędy naprawić.
Kontinuum - to jest JEDNO, identyczne jakościowo z samym sobą i powielone ilościowo w nieskończoność.
Kontinuum - jako JEDNO powielone w nieskończoność - może znajdować się w takim samym - identycznym fizycznie stanie oraz/lub w różnych stanach - zróżnicowanych fizycznie.
Kontinuum - to jedno jakościowo, ciągłe i powielone ilościowo.
Obiekty- to jedno jakościowo powielone ilościowo, ale różnorodne i zróżnicowane fizycznie.
Zwykle do obserwacji klasycznej używana jest albo płaszczyzna euklidesowa 2D albo przestrzeń euklidesowa 3D. Ale w obu przypadkach: płaszczyzna i przestrzeń charakteryzują się krzywizną zerową. Przez to światu fizycznemu narzucamy pewne prawa, które obowiązują w płaskim, ze względu na krzywiznę zerową, świecie. Jednakże obiekty mogą charakteryzować się zmienną lub zróżnicowaną krzywizną. I tak na przykład okrąg ma krzywiznę równą 1. Krzywizna okręgu jest w każdym punkcie jednakowa i równa odwrotności jego promienia. Czyli jeśli zmienia się wartość promienia, to krzywizna okręgu powinna ulegać zmianie. Jeśli zaś wartość promienia jest ustalona na jednostkową r = 1, wówczas krzywizna badana wzdłuż promienia powinna się zmieniać w ten sposób, że im bliżej hipotetycznego środka promienia, tym krzywizna będzie malała aż do zera. Przypomnę, że pisałam kiedyś o tym, iż dualizm korpuskularno-falowy jest po prostu dualizmem obserwacyjnym. Wynika z dwóch różnych sposobów prowadzenia obserwacji tego samego obiektu. Przykład prosty : okręgi.
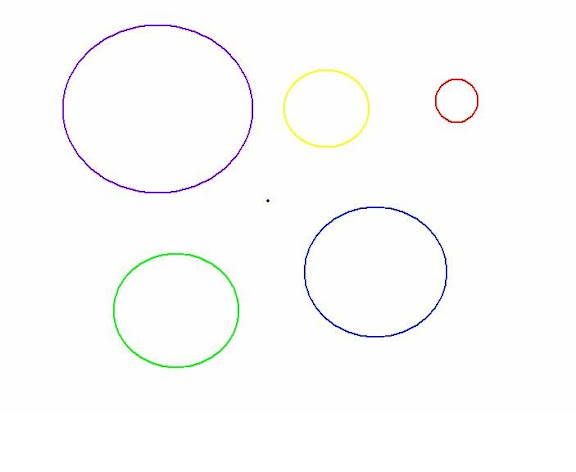
Mamy dwa sposoby obserwacji okręgów:
1. Obserwujemy te wszystkie okręgi jako różne, ponieważ uwzględniamy ich zmienne: długość L i promień r.
Te wszystkie okręgi (łącznie z punktem-kropką między nimi) możemy uznać za różne okręgi, pod warunkiem, że przypisujemy im krzywiznę zerową - określamy w ten sposób poziom klasyczny obserwacji. Wówczas wszystkie okręgi mają różny promień, a wszystkie opisywane są poprzez wzór:
L = 2 Pi r, w którym wartości promienia "r" i obwodu „L” są zmienne.
„L” i „r” są wprost proporcjonalne: gdy zwiększa się promień, zwiększa się też obwód.
W tym przypadku obserwujemy okręgi jako różne obiekty. Różnicuje je różna wartość promienia i obwodu. Jednak przy tej obserwacji przyjęto, że krzywizna dla każdego z tych okręgów jest stała.
Analogicznie w fizyce cząstek możemy przekształcić wzór na okrąg w ten sposób, że:
p (pęd) = 2 Pi v
p (pęd) i „v” prędkość wektorowa są wprost proporcjonalne: gdy zwiększa się pęd, zwiększa się też prędkość wektorowa.
Stąd
v = p /2 pi
2. Obserwujemy te wszystkie okręgi jako jeden okrąg znajdujący się w różnych stanach, ponieważ uwzględniamy ich zmienne oraz ukryte stałe.
Te wszystkie okręgi oraz punkt możemy uznać za różne stany jednego i tego samego okręgu, który będę nazywać meta-okręgiem o zmiennej krzywiźnie – w ten sposób określalibyśmy kwantowy sposób obserwacji.
L = k * 2 Pi R/n
W tym wzorze „ n”– wyznacza ilość pod-okręgów składających się na cały i stały obwód L. Natomiast "k" - wyznacza zmienną krzywiznę całego układu podokręgów i odpowiada ich ilości.
Przy obserwacjach dokonywanych na dowolnej z trzech płaszczyzn euklidesowych o zerowej krzywiźnie, stały promień – wektor jest łamany na pod-promienie – wektory czyli R/n = r.
W swojej notce – artykule pt. GEOMETRIA BLIŻEJ FIZYKI KWANTOWEJ część 2.” pisałam również o zmianach długości promienia zależnych od zmiany krzywizny przestrzennej okręgu:
Dla każdego z obu małych okręgów wartości L i R zmalały o połowę. Przy okazji zjawiska skręcania gumki występuje geometryczne zwiększenie krzywizny polegające na zwielokrotnianiu się pod-okręgów. W takim przypadku dla każdego z podokręgów długość okręgu i promienia maleją proporcjonalnie w zależności od ilości podokręgów znajdujących się we wspólnym układzie zachowującym stały obwód L i promień: L = 2 x 2 π rR/2, L= 3 x 2 π R/3, L= 4 x 2 π R/4 itd…
Rysunek 2. jest przykładem dla stanu okręgu opisanym jako L = 3 x2 π R/3:
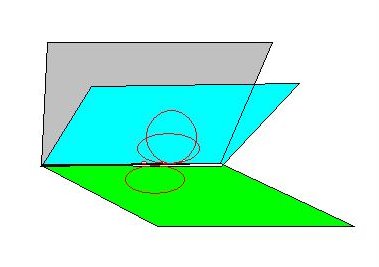
Aby uwzględnić zmiany geometrii okręgu zachodzące w przestrzeni, zastosowałam dodatkowy parametr – stałej ukrytej L uwzględniający zmiany stanu okręgu. Natomiast promień przyjmuję za zmienny po to, aby zaistniała możliwość obserwacji zjawiska, które ma miejsce w przestrzeni poza płaszczyzną euklidesową.
W takim przypadku R/n = r. Stąd wzór:
L = k * 2 Pi r
uwzględnia stały obwód meta-okręgu i zmienny promień charakterystyczny dla zmiennych stanów meta-okręgu.
W tym wzorze „ k” – wyznacza zmienne wartości krzywizny uwzględniające zmiany geometrii okręgu.
Wówczas meta-okrąg ma stały obwód, ale poszczególne stany tego meta-okręgu możemy opisywać dzięki zmiennej krzywiźnie przestrzennej meta-okręgu poprzez wzór:
L = k * 2 Pi r, w którym wartości krzywizny przestrzennej "k" oraz wartości promienia „r” są zmienne i odwrotnie proporcjonalne względem siebie, ale wartość obwodu okręgu jest stała.
W tym przypadku obserwujemy różne stany jednego obiektu – różnicuje je wartość krzywizny jego przestrzeni. Czyli mamy do czynienia z jednym okręgiem o zróżnicowanej wartości promienia. Podobnie jest z "cząstkami elementarnymi". Są one po prostu stanami jednej meta-cząstki.
Analogicznie:
p (pęd) = k * 2 Pi v
Tutaj „k” i „v” są odwrotnie proporcjonalne: gdy zwiększa się „k”, zmniejsza „v”. Pęd pozostaje stały, na przykład p = c. Przy stałym pędzie dla wzrastającej krzywizny prędkość wektorowa się zmniejsza, a przy zmniejszającej się krzywiźnie, prędkość wektorowa się zwiększa. Stąd:
c = k * 2 Pi v
oraz
v = c/ k * 2 Pi
Natomiast zmienność pędu wynika ze zmiany energii takiego pola grawitacyjnego, co możemy zaobserwować i opisać przy pomocy zmiany geometrii tego pola grawitacyjnego.
Oto mamy pole grawitacyjne o sferycznej geometrii:
S = 4 Pi r²
Wyobraźmy sobie, że zderzają się ze sobą dwie meta-cząstki:
4 Pi r² + 4 Pi r² = 8 Pi r²
A ponieważ przyjęłam, że
p (pęd) = 2 Pi v,
to analogicznie teraz mamy:
c² + c² = 4 Pi v² + 4 Pi v² = 8 Pi v²
A stąd:
2 c² = 8 Pi v²
oraz:
c² = 8 Pi v²/2
I zaobserwujmy teraz, co dzieje się wówczas z pędem i krzywizną takiej cząstki. Można zauważyć, że krzywizna przestrzeni meta-cząstki uległa zmianie, ponieważ teraz zamiast:
p (pęd) = 2 Pi v
mamy:
p²= 8 Pi v²/2
Gdy będziemy obserwować pęd takiej cząstki, to okazuje się, że dla stałego pędu mamy:
c²= 8 Pi v²/2
inaczej (ogólnie):
c²= k x 2 Pi v²/2
czyli teraz możemy określić pęd jako:
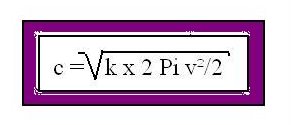
Mamy jakieś jedno pole jako 8 Pi v²/2 czyli dwa pola zespolone jako 2 x 4 Pi v². Jest to obserwacja uwzględniająca zmiany krzywizny przestrzennej meta-cząstki. Jak to możliwe? Ano możliwe. Na przykład tak:
Rysunek 3
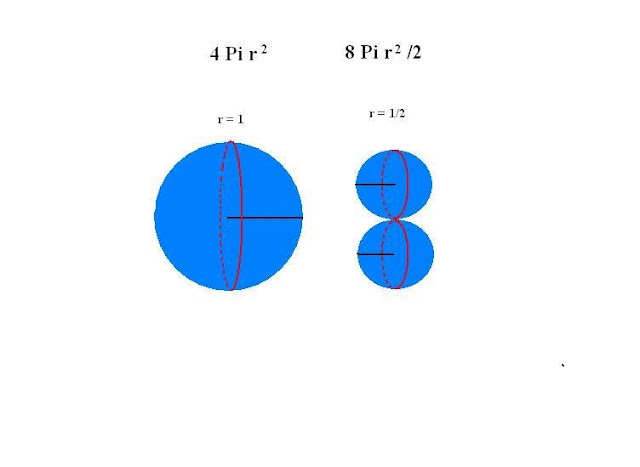
Ten rysunek zestawię teraz z rysunkiem Bernarda Jacewicza z jego wykładu pt.: „Skalary, wektory i co dalej?” (http://www.if.uj.edu.pl/Foton/103/pdf/06%20skalary.pdf)
Rysunek 4

Może teraz komuś uda się wreszcie dostrzec, dlaczego uznałam, że „fotony” mają swoje własne pole grawitacyjne, które wygląda w ten sposób:
Rysunek 5
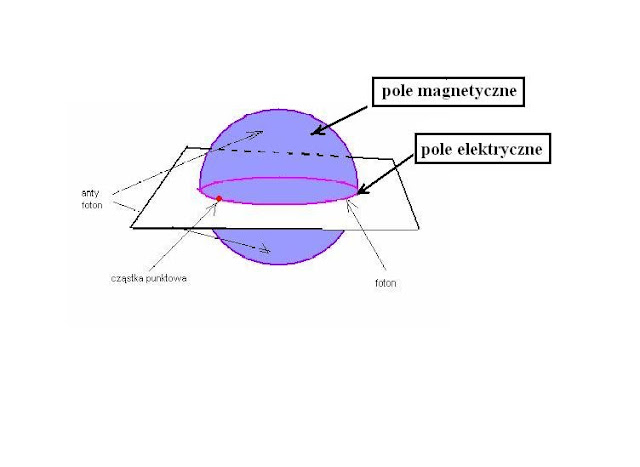
Następne możliwości obserwacji dla r = v = 1:
Rysunek 6
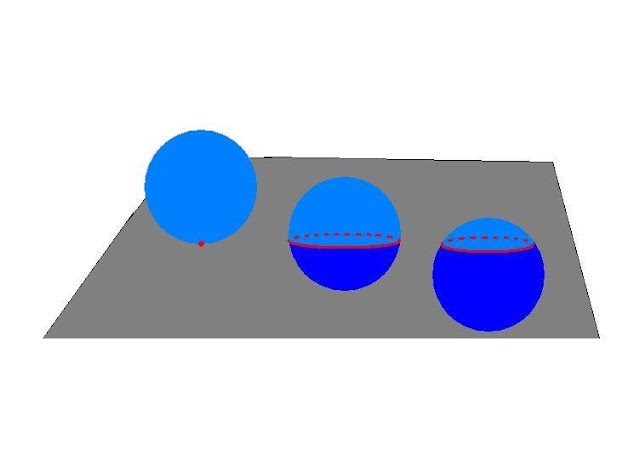
Teraz obserwujemy różne okręgi na płaszczyźnie – geodezyjne o zróżnicowanym promieniu.
Także okrąg może zmieniać stan w wymiarze krzywizny tak, że zamiast jednego pojawiają się dwa o różnym promieniu, w ten sposób, że wewnątrz jednego okręgu pojawiła się pętla w formie drugiego okręgu. Bąbel w bąblu.
Rysunek 7
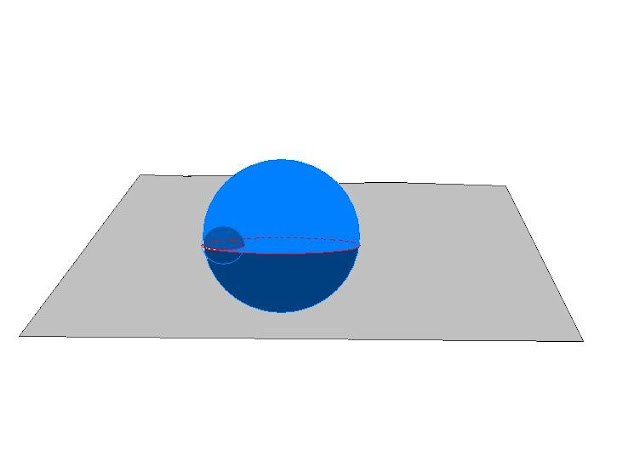
Taki stan określiłam jako turbulentny.
Na rysunkach 5 i 6 przedstawiłam, jak może wyglądać hipotetyczne pole grawitacyjne meta-cząstki o promieniu wektorowym v = 1. Teraz przedstawię, jak może wyglądać pole grawitacyjne meta cząstki dla której wartość wektora prędkości v wynosi połowę: v = ½. Oto przykład dla r = v = 1/2:
Rysunek 8
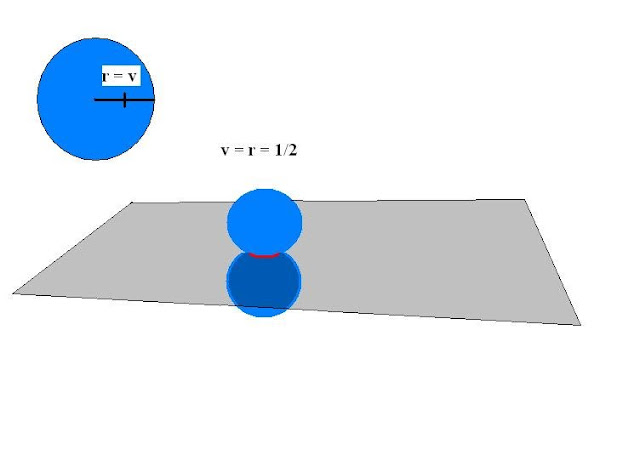
Można teraz się zastanowić, jak wyglądałoby pole magnetyczne dla dwóch, trzech oraz "n" meta-cząstek. Można także wyobrazić sobie, jak te pola tworzą całe układy pól, jak tworzą wspólne pola... Jak w kontinuum jakościowym tworzą się gęstki z powodu powielenia ilościowego takich cząstkek i całe układy grawitacyjne, które wówczas współtworzą. Tak mogą wyglądać oddziaływania grawitacyjne na poziomie cząstek energetycznych. Można wyobrazić sobie całą ogromną dynamikę zmian stanów pól grawitacyjnych i geometrycznej zależności pól sił elektrycznych i magnetycznych.

" Rzeczywistość składa się z nieskończonego strumienia interpretacji postrzegania, które my, jednostki posiadające specyficzne członkostwo nauczyliśmy się odczuwać jako oczywiste. (...) Nasz odbiór rzeczywistości jest przez nas uznawany za tak niepodważalny, że podstawowe założenie magii traktujące go jedynie jako jeden z wielu opisów, niełatwo przyjąć poważnie."
" Don Juan - człowiek wiedzy i nauczyciel Carlosa Castanedy. -------------------------------------------------
dodatek z dnia 13.09.09
"Każdy człowiek tworzy swoją osobistą historię ze swojej własnej i jedynej w swoim rodzaju perspektywy. Po co w takim razie narzucać innym swoją wersję, jeśli będzie ona dla nich nieprawdziwa? Kiedy to zrozumiesz, nie będziesz odczuwać potrzeby obrony tego, w co wierzysz. Nie jest ważne to, aby mieć rację i dowieść innym, że są w błędzie. Postrzegaj każdego człowieka jako ARTYSTĘ, kogoś, kto ma ci do opowiedzenia jakąś historię. Wiedz, że to, w co wierzą inni, jest po prostu ich punktem widzenia, i że nie ma to z Tobą nic wspólnego." Don Miguel Ruiz
-------------------------------------------------
--------------------------------------------------
Moje notki "unifikacyjne":
1. Geometria kwantowa 1
2. Geometria kwantowa 2
3. Geometria Kwantowa 3 -wstęp do kwantowej grawitacji
4. Geometria kwantowa 4
5. Torusy
6. Prędkość grawitacyjna a stała Plancka
7. Kwanty światła i eter - część I.
8. Kwanty światła i eter - część II.
pozostałe notki w polecane strony
Nowości od blogera
Inne tematy w dziale Technologie

