Mechanizm obrotu ciał sztywnych

    Przy ostatniej mojej notce gdzie pokazałem mechanizm powstawania i działania przyspieszeń kontowych został on skomentowany przez czytelnika KK-54, sugerujący nie po raz pierwszy że przy "fikołku gaiki" (termin często używany na salon24) to gwint z którego zsuwa się gaika nadaje jej specyficzny ruch i efektowny fikołek. Chociaż oczywiście gwint nadaje gaice jakiś stan początkowy czyli częściowo KK-54 ma racje, to sam gwint nie ma nic wiele wspólnego z tym co dzieje się później. Innym terminem opisującym ten ruch jest teoria rakiety tenisowej, nazwana tak dlatego że tenisiści jakiś czas temu zauważyli że podczas podrzucania z obrotem rakiety tenisowej, obrót wokół jednej z osi jest jak to nazwali "niestabilny". Jak widać no poniższym filmiku rakieta tenisowa tez "fika" mimo że do nadania jej wartości początkowych nie używamy żadnego gwintu

    W tej notce postaram się lepiej wyjaśnić co właściwie się dzieje podczas obrotu ciała sztywnego. Bryła sztywna to oczywiście cała masa punktów ale przy wyjaśnieniu tego zjawiska możemy zastosować duże uproszczenie. Jak się okazuje jeżeli bryły sztywne mają te same główne momenty bezwładności (oto jak je wyznaczamy https://www.youtube.com/watch?v=igZOi_IZjuY )to kształt bryły jak i rozmieszczenie jej punktów nie ma wpływu na ten ruch. Oznacza to że dowolną skomplikowaną bryłę sztywną możemy uprościć do prostszego modelu o tych samych głównych momentach bezwładności i obydwie te bryły podczas obrotu będą się zachowywać identycznie. Oczywiście kształt i rozmieszczenie mają wpływ na działanie sił wewnętrznych działających na poszczególne punkty ale bryła jako całość będzie się zachowywać identycznie.

    Aby zrozumieć jak to działa przyjrzyjmy się takiej sytuacji

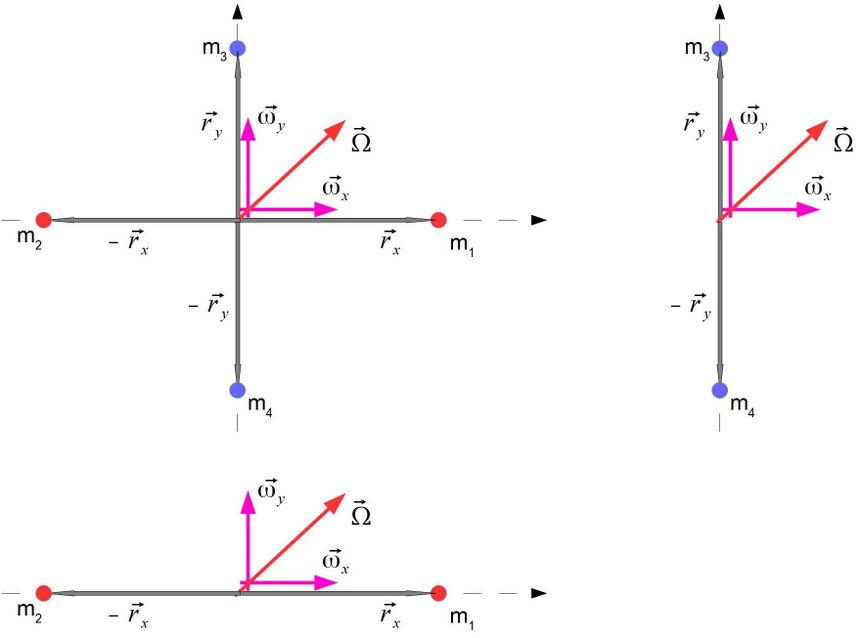
    Wyidealizowana najprostsza bryła sztywna. Dla uproszczenia przyjmijmy że wartość wektorów położenia jest taka sama r_y=r_x i że masy punktów na tej samej osi są równe m₁=m₂ i m₃=m₄. Jak widać na schemacie każdy punkt ma dwie składowe wektora prędkości, jedną prostopadłą do wektora położenia a druga jest równoległa, z tą różnica że dla punktów na osi X składowa prostopadła to ω_y a składowa równoległa to ω_x a dla punktów na osi Y sytuacja jest odwrotna.

    Składowa wektora prędkości kątowej determinuje wektory prędkości punktów

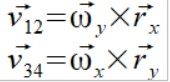    (1)

    Stosując regułę prawej dłoni możemy sprawdzić że punkty na tej samej osi mają wektory prędkości w tym samym kierunku i jednocześnie w przeciwnym kierunku niż punkty na drugiej prostopadłej osi.

    Dodatkowo wszystkie punkty mają składową prędkość kątową równoległą do wektora położenia który powoduje obrót punktów wraz z ich wektorami prędkości

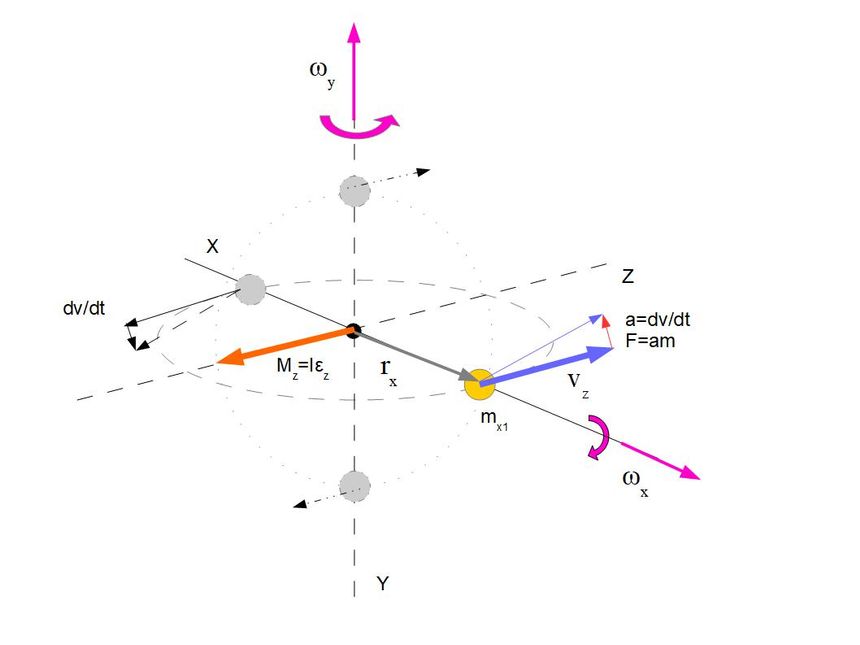
A wektor przyspieszenia liczymy ze wzoru na przyspieszenie kątowe

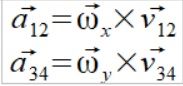    (2)

    Przyspieszenia te powodują zaistnienie momentów sił i również tutaj punkty na jednej osi powodują powstanie momentów sił o tym samym kierunku i jednocześnie są one przeciwne momentom sił generowanych przez punkty znajdujące na drugiej prostopadłej osi.

    Ponieważ dobrałem odpowiedni układ odniesienia mogę teraz zastosować wzory Eulera

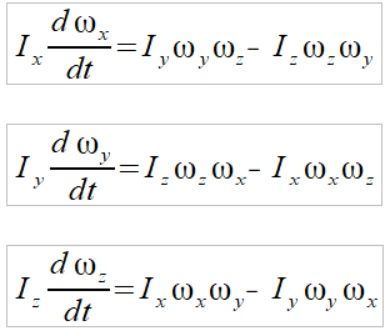    (3)

czyli mamy

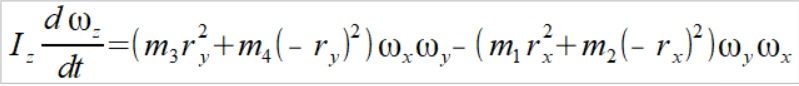
    Pamiętajmy że w tym przykładzie wektory położenia mają tą samą wartość r_y=r_x i że masy punktów na tej samej osi są równe m₁=m₂ i m₃=m₄.

    Rozpiszmy więc te momenty siły. Zauważmy że jest tu wzór (1) i (2)

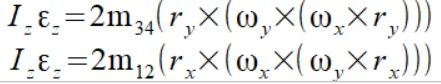
    Pamiętajmy że własność iloczynu wektorowego powoduje że te dwa momenty sił mają przeciwny zwrot i jeżeli wektory położenia maja tą samą wartość to wynik iloczynu wektorowego w nawiasach również będzie miał ta samą wartość. W tym przypadku jeżeli masy na obu osiach będą równe to powstałe momenty sił się wyzerują jednak jeżeli masy na jednej osi będą inne niż na tej drugiej to powstanie niezerowy moment siły.

    Reasumując odpowiedź na komentarz KK-54, to czy gaika zsunęła się z gwintu czy też czy tez została wprawiona w ruch obrotowy w jakiś inny sposób nie ma większego znaczenia. Patrząc na wzór (3) istotna jest różnica głównych momentach bezwładności Ix≠Iy≠Iz ponieważ jeżeli któreś są takie same to zerują poszczególne równania i istnienie co najmniej dwóch składowych prędkości kątowych w układzie odniesienia głównych momentów bezwładności. Gdy zostaną spełnione te warunki to zawsze powoduje to powstanie niezerowego przyspieszenia kątowego które jednak nie zawsze są tak efektowne jak efekt Dzanibekowa. Efekt ten "koziołek" powstaje gdy ciało sztywne obraca się wokół pośredniego momentu bezwładności niezależnie jak bryła sztywna została wprawiona w ruch obrotowy.