Przez ostatnie dwa tygodnie ostro wziąłem się za wgryzanie się w pochodną równania momentu pędu

Bardzo dużo żmudnych obliczeń najpierw ręcznie, bo zapis na karetce poszczególnych rozwiązań pozwala na dokładne prześledzenie etapów oddziaływań i powiązań poszczególnych zmiennych na siebie. Ułatwia to leprze zrozumienie co się dzieje w równaniu i jak ono działa. Niestety liczenie ręczne ma swoje ograniczenia, zazwyczaj biorę przypadki szczególne aby było jak najwięcej zer i liczby były jak najprostsze aby ułatwić obliczenia, przez co zawsze istnieje spore ryzyko że rozwiązanie będzie działać dla tego przypadku szczególnego ale nie będzie działać w innych przypadkach, gdzie pewne detale się nie będą zerować i wpływać na poprawność wyniku. W matematyce nie ma miejsca na improwizacje czy jakieś niedociągnięcia, każdy najmniejszy błąd lub pominięcie które może wydawać się blachę powoduje rozsypanie się wyniku. Jeżeli jest jeden błąd to przy rozpisaniu ręcznym łatwo go wypatrzyć, jeżeli błędów jest kilka to wyłapywanie ich jest istnym koszmarem. Po za tym szybko liczyć to ja potrafiłem w szkole średniej i na studiach a po wielu latach niepraktykowania tych umiejętności obecnie często się zacinam na prostych rzeczach które po prostu się pozamykało.
Oto moje obliczenia na papierze tylko z ostatnich dwóch tygodni, wszystkie kartki są zapisane dwustronnie

Po liczeniach ręcznych które dały pozytywną weryfikacje zacząłem testować te rozwiązania na algorytmach i załamka. Dla przypadków szczególnych algorytm działał ale dla innych przypadków wynik się sypał, wielokrotnie sprawdzałem algorytm i nie mogłem się dopatrzyć błędu i wszystko wskazywało na to że zastosowane rozwiązania nie są zawsze poprawne. Po ochłonięciu kolejne sprawdzenie i w jednym miejscu był + zamiast - a że kopiowałem tą linijkę to i powielałem ten błąd, po korekcie wszystko zaczęło działać.
I w końcu jest pochodna która jest bardzo obiecująca i którą obecnie testuje na algorytmach komputerowych.
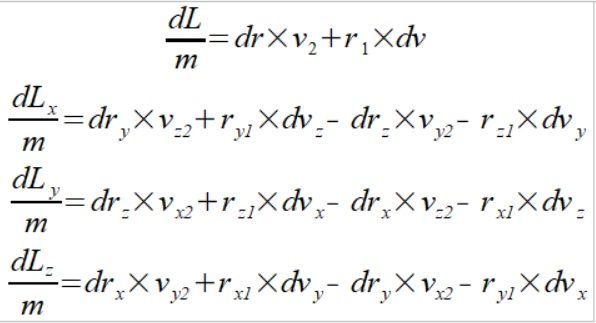
Jest to pochodna dla jednego punku gdzie Indeksy 1 jest to stan dla t1, indeks 2 jest to stan dla t2. Po rozłożeniu wektora prędkości v na prędkość kątową i wektor promienia uzyskamy równanie tensora ale nie jestem jeszcze pewien jak to zrobić dlatego nie będę tego robił w tej notce.
Dla pojedynczego punktu spisuje się doskonale, liczę na konkretnych przykładach i niestety algorytm musi stosować zaokrąglenia ale największy błąd był do -12 czyli do jednej bilionowej a najczęściej są to błędy rzędu do -15 czyli jednej trylionowej albo mniejsze.
Moje algorytmy obrotu ciała sztywnego przy stosunkowo dużym dt=0.01 dają błędy rzędu do -4 i suma pochodnych dl dla punktów takiego ciała sztywnego również generuje błędy tego rzędu ale myślę że jak poprawie algorytm obrotu ciała sztywnego to również błąd pochodnej zmniejszy się do poziomu który będzie można uznać za nieistotny.
Jeżeli ktoś ma pomysł jak sprawdzić skuteczność tej pochodnej lub umiał by to zrobić to będę wdzięczny za każdą podpowiedź.








Komentarze
Pokaż komentarze (7)