Gdy element który szacowałem że wyliczę w dwa dni ziają mi ponad trzy tygodnie, to wkurzyłem się na siebie i zeszło ze mnie powietrze. Niestety w ludzkim świecie akt kreacji odznacza się dużym niezrozumieniem, obojętnością i samotnością, sukces za to ma wielu ojców.
Jest to irytujące że mam już sporo interesujących wyników i rozwiązań które bardziej wnikliwie i dokładniej pokazują detale obrotu ciał sztywnych, a mimo wszystko fakty te są w najlepszym przypadku ignorowane a często traktowane z wrogością jako herezja. Wielu zarzuca mi że rozwiązania te są niesprawdzone i niezgodne z prawami fizyki, a prawda jest taka że wiele elementów zostało prze zemnie pozytywnie zweryfikowane i udowodnione i to oskarżyciele zakładają z góry że to ja się mylę i nie dokonali żadnych weryfikacji swoich tez tylko z góry oceniają je jako błędne. Jakby ci co twierdzą że moje rozwiązania są błędne zechcieli to zweryfikować, szybko by się przekonali że są one niezbędne aby prawa fizyki utrzymać, czyli moja praca jest rozwinięciem obecnej wiedzy a nie jej "obalaniem".
W poprzedniej notce zaprezentowałem pochodną momentu pędu gdzie indeks 1 jest dla chwili t1, a indeks 2 dla chwili t2
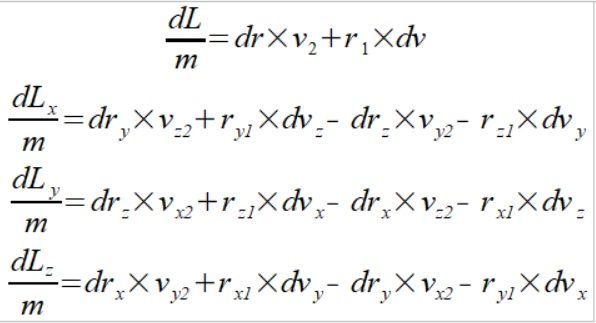
Teraz krótki algorytm sprawdzający, w jaki sposób weryfikuje praktyczne zastosowanie tego wzoru dla pojedynczego swobodnego punktu. Takim punktem może być dowolne ciało niebieskie będące na orbicie obracające się wokół środka ciężkości układu. O ile nie wystąpią oddziaływania zewnętrze to wektor momentu pędu takiego punktu jest stały, czyli pochodna tego wektora równa się zero. Język Vpython.
from visual import *
m=3
r=vector(2,0,0)
w1=vector(0,3,4)
dt=0.5
dt2=0.8
print "r0", r, mag(r), "w", w1
r=r.rotate(angle=mag(w1)*dt,axis=w1)
print "r1", r, mag(r)
v=cross(w1,r)
p=m*v
L=cross(r,p)
print "L", L, "v", v, "p", p
Ixy=-m*r.x*r.y
Ixz=-m*r.x*r.z
Iyz=-m*r.y*r.z
Ixx=m*(r.y*r.y + r.z*r.z)
Iyy=m*(r.x*r.x + r.z*r.z)
Izz=m*(r.x*r.x + r.y*r.y)
Ls=vector(w1.x*Ixx+w1.y*Ixy+w1.z*Ixz,w1.x*Ixy+w1.y*Iyy+w1.z*Iyz,w1.x*Ixz+w1.y*Iyz+w1.z*Izz)
print "Iw", Ls #sprawdzenie poprawnosci tensora
r2=r.rotate(angle=mag(w1)*dt2, axis=w1)
v2=cross(w1,r2)
p2=m*v2
#p2=p2*4 #zewnetrzny moment sily
v2=p2/m
F=mag(p2)-mag(p) #sila z przyspieszenia stycznego
M=mag(r2)*F
print
print "v2", v2, "p2", p2
print "M", M
print "****************"
print "dL_x/dt = dr_y*m*v_z2 + r_y1*m*dv_z - dr_z*m*v_y2 - r_z1*m*dv_y"
#print "dL_x/dt=", r2.y-r.y,m*v2.z,"+",r.y,m*(v2.z-v.z),"-",r2.z-r.z,m*v2.y,"-",r.z,m*(v2.y-v.y)
print "dL_x/dt=",m*(((r2.y-r.y)*v2.z)+(r.y*(v2.z-v.z))-((r2.z-r.z)*v2.y)-(r.z*(v2.y-v.y)))
print "dL_y/dt = dr_z*m*v_x2 + r_z1*m*dv_y - dr_x*m*v_z2 - r_x1*m*dv_z"
#print "dL_y/dt=", r2.z-r.z,m*v2.x,"+",r.z,m*(v2.x-v.x),"-",r2.x-r.x,m*v2.z,"-",r.x,m*(v2.z-v.z)
print "dL_y/dt=",m*(((r2.z-r.z)*v2.x)+(r.z*(v2.x-v.x))-((r2.x-r.x)*v2.z)-(r.x*(v2.z-v.z)))
print "dL_z/dt = dr_x*v_y2 + r_x1*dv_y - dr_y*v_x2 - r_y1*dv_x"
#print "dL_z/dt=", r2.x-r.x,m*v2.y,"+",r.x,m*(v2.y-v.y),"-",r2.y-r.y,m*v2.x,"-",r.y,m*(v2.x-v.x)
print "dL_z/dt=",m*(((r2.x-r.x)*v2.y)+(r.x*(v2.y-v.y))-((r2.y-r.y)*v2.x)-(r.y*(v2.x-v.x)))
Można sobie go skopiować i uruchomić. Można wpisywać dowolną masę i dowolny wektor położenia r i prędkości kątowej w, pod warunkiem że wektory te będą do siebie prostopadłe. Aby sprawdzić czy wektory są prostopadłe należy dokonać iloczynu skalarnego r na w i uzyskać zero. Jest to warunek niezbędny dla swobodnego punktu, gdyż dla takich punktów wektory te są zawsze prostopadłe. Aby policzyć inne przykłady trzeba rozbudowywać algorytm i staje się on coraz bardziej zagmatwany, a publikacje na blogu wymagają podawania możliwie najprostszych przykładów aby jak największa rzesza odbiorców była w stanie je zrozumieć.
Aby pokazać skuteczność wzoru pierwotny wektor może być obrócony dwa razy, linijka 10 i 28. Dlatego też mamy dwa odcinki czasu dt i dt2. Jeżeli chcemy obrócić nasz wektor tylko raz należy wpisać wartość pierwszego odcinak czasu jako zero, dt=0.
Mamy też możliwość wprowadzić zmianę pędu punktu (linijka 30) co symuluje działanie zewnętrznego momentu siły, który jest wzdłuż wektora momentu pędu. Zmiana wielkości wektora pędu punktu jest wynikiem działania niezerowego momentu siły i moja pochodna również poprawnie go wylicza.
Największy błąd jaki dostałem był 10^-12 czyli jest to w przybliżeniu 0,000000000001 a często ten błąd jest jeszcze dużo mniejszy. Dokonywałem też sporo weryfikacyjnych wyliczeń na konkretnych przykładach przy zmianie długości wektora położenia ale trzeba wtedy dodać wektor przyspieszenia jaki uzyskuje ciało wyniku zmiany momentu bezwładności, czy też działanie momentu siły prostopadłego do wektora momentu pędu. Żaden z przykładów który sprawdzałem nie wykazał większego błędu niż 10^-12 który to błąd uważam na tyle mały że jest on wynikiem zaokrągleń i jest nieistotny.
Weryfikacje dla pojedynczego punktu uważam za pozytywną, problem jest niestety z ciałem sztywnym gdyż dla niej zmiana wektora prędkości kątowej nie jest wartością stałą a jest dość skomplikowaną funkcją. Nie dość że zmiana prędkości kątowej występuje w różnym tempie to jeszcze wraz ze zmianą momentu bezwładności zmienia się też jej wartość i również w różnym tempie.
Niestety algorytmy które do tej pory stosowałem generują błędy na tyle duże że są bezużyteczne do weryfikacji tej pochodnej, po prostu błąd się na tyle sumuje że wynik mnie nie satysfakcjonuje. Niestety muszę wymyślić coś innego a to znów jest sporo pracy.








Komentarze
Pokaż komentarze (7)