Niestety licząc po nocach dopuściłem się strasznych błędów rachunkowych. Na szczęście mimo że rachunki były złe, to po ich poprawieniu wynik pozostał ten sam. Liczenie po nocach i pisanie wyników na siłę niestety czasami się tak kończy. Na szczęście błędy wychwycone i poprawione, można iść dalej. Obecnie symuluje metodę ze skutkiem pozytywnym, napiszę o tym wkrótce.
Niestety we wzorach był błąd na żółto zaznaczona korekta.
Przedstawione poniżej wywody i rozwiązania są tylko wstępną koncepcją. Niestety temat jest bardzo skomplikowany i sprawdzenie wszystkich konfiguracji bryły sztywnej oraz udowodnienie że takie rozwiązania odpowiadają rzeczywistości, wymaga jeszcze sporo czasu i pracy. Dobierałem tak konfiguracje by łatwo można było sprawdzić poprawność hipotez ale nie mam pewności że w innych konfiguracjach moje pomysły też się sprawdzą.
Wielu Fizyków twierdzi że moje tezy stoją w sprzeczności z obecną wiedzą, nikt nie przedstawia na to dowodów. Za to ja znajduje w materiałach naukowych coraz więcej faktów które negują argumenty moich krytyków. Cząstkowe szacowanie tematu, bez dokładnego poznania szczegółów powodują to, że zapewne nieświadomie to moi krytycy używają argumentów sprzecznych z obecną widzą. Jak do tej pory nie znalazłem sprzeczności moich założeń z obecną wiedzą, wręcz przeciwnie coraz więcej detali się potwierdza.
Ponieważ w mechanice klasycznej wszystko jest względem układu odniesienia, dlatego bardzo ważne jest dobranie odpowiedniego układu współrzędnych. Oczywiście mechanika klasyczna pozwala na rozpatrywanie każdego zagadnienia w każdym układzie odniesienia ale pod warunkiem że umiemy prawidłowo dokonać transformacji między układami. Dobranie odpowiedniego układu odniesienia pozwala dokonać obliczeń znacznie prościej aniżeli w innych układach.
Pytanie jest który układ odniesienia jest najłatwiejszy i prawidłowy dla rozpatrywania zagadnienia swobodnego obrotu bryły sztywnej? Straciłem pół dnia na znalezienie jakiegoś dowodu lub definicji, stwierdzenia w podręcznikach czy w jakiejś pracy profesorskiej, że układ odniesienia gdzie 0 pokrywa się ze środkiem ciężkości jest tym właściwym ale nie znalazłem. Wszędzie piszą że powinien to być ten układ ale nie znalazłem żadnych uzasadnień dlaczego ten a nie inny. Większość materiałów o mechanice jest napisane pod urządzenia ziemskie, gdzie ruch obrotowy swobodny jest bardzo rzadki a większość urządzeń działa z punktami podparcia, dlatego też tak trudno jest znaleźć informacje które mi są przydatne.
Więc może krótko po swojemu, podam swoje argumenty dlaczego właśnie ten układ jest niejako podstawowy. W podręczniku znalazłem taką definicje:
„Mechanika klasyczna” M. Klasztorny ISBN 978-83-7125-271-6
str 244 tw 25
„Zasada zachowania ruchu środka masy
Jeżeli siła ogólna S(t) jest tożsamościowo równa zeru, to środek masy C układu punktów materialnych jest w ruchu jednostajnym prostoliniowym lub jest nieruchomy.”
W mechanice klasycznej przy ruchu obrotowym bardzo ważne są pseudo-wektory wynikające z iloczynu wektorowego. Mamy moment siły M=rxF, mamy kręt L=rxp mamy prędkość kątową którą musimy policzyć trochę inaczej v=ωxr itp. Sprawne oko zauważy że przy wyliczeniach tych pseudo-wektorów bardzo ważny jest wektor pozycji r, zwany też wektorem wodzącym. Oznacza to że moment siły czy kręt jest zależny od punktu odniesienia. Rzeczywisty Moment siły czy kręt dla bryły sztywnej, można wyliczyć bezpośrednio z tych wzorów bez żadnych dodatkowych działań, jedynie w układzie odniesienia gdzie 0 znajduję się w środku ciężkości. Dlatego też zakładam że to środek ciężkości jest punktem wokoło którego powstają wszystkie zależności i to on powinien stanowić podstawę do wyznaczania wektora r. Czy ten punkt jest również punktem odniesienia do wektora prędkości kątowej? Sprawa jest nieco skomplikowana gdyż r ze wzoru na prędkość kątową musi być prostopadły do wektora ω. Oznaczało by to że w BS różne punkty mogą mieć różne "prawidłowe" układy odniesienia. Ale czy nie da się sprowadzić wszystkiego do jednego punktu w środku ciężkości? Aby to zrozumieć musimy wiedzieć więcej.
„Mechanika” W. Tybor, K. Kowalski. ISBN 978-83-8088-251-5
str 120
Układ środka masy jest to układu współrzędnych gdzie początek wybieramy w punkcie 0c w którym to znajduje się środek masy.
str123 roz 4.1.2 ruch środka masy
„… b) Siła Fij jest siłą wewnętrzną opisującą oddziaływanie cząstki j na cząstkę i...
Dalej będziemy zakładać, że siły wewnętrzne opisujące oddziaływanie punktów materialnych a i b są centralnymi siłami newtonowskimi (spełniają III zasadę dynamiki Newtona Fij=-Fji i działają wzdłuż prostej łączące obie cząstki.)
Jeżeli dalej przyjmiemy, że wartość sił wewnętrznych zależy tylko od odległości rij punktów materialnych i i j … (schematy i wzory)
… Widzimy że siły są centralne (działają wzdłuż wektora rij i spełniają III zasadę dynamiki)...
Dla centralnych sił Newtonowskich
Σfij=0”
Chociaż w wielu materiałach jest stwierdzenie że siły więzów są siłami centralnymi, czyli są skierowanymi do środka ciężkości wielu bardzo dobrych Fizyków temu zaprzecza. Nikomu nie chce się tego sprawdzić, dlatego lepiej jest wyzywać mnie od nieuka i tak mi nikt nie uwierzy. Bardzo trudno jest dojść do jakiegoś porozumienia z osobami które porozumieć się nie chcą.
Wróćmy jednak do tematu. Jak za pomocą wektora wodzącego zaczepionego w środku ciężkości uzyskać wektor prędkości kątowej?
Bryła sztywna jest to zbiór punktów materialnych które nie mogą się względem siebie przemieszczać. Istnieją siły więzów które trzymają punkty materialne względem siebie nieruchomo i jak mówi obecny stan wiedzy przy obrocie BS siły te są skierowane do środka ciężkości.
Zobaczmy teraz jak wygląda mechanika obrotu dwóch punktów połączonych ze sobą siłą więzów.
m1(√2,√2,0); r1=2; z prędkością v1(0,0,-2)
m2(-√2,-√2,0); r2=2; z prędkością v1(0,0,2)
środek ciężkości (0,0,0)
W poprzedniej notce ustaliłem proporcje dla prędkości kątowej swobodnego punktu
ω = 1/r x v (1)
https://www.salon24.pl/u/przestrz/804906,predkosc-katowa-fizyki-nie-da-sie-zrozumiec-trzeba-ja-wyliczyc,2
r1=2
1/r1=(√2/2,√2/2,0)
Dlatego też dla każdego punktu mogę szybko wskazać wektor ω.
ω1=(-√2/2, √2/2, 0)=ω2=1
Widzę pewną prawidłowość średnia prędkość kątowa to
ω=(Σn(ωn))/n (2)
Czy to działa też w innych przypadkach? Rozpatrzmy więc drugi układ do pierwszego prostopadły.
m3(-√2,√2,0); r1=2; z prędkością v1(0,0,-2)
m4(√2,-√2,0); r2=2; z prędkością v1(0,0,2)
środek ciężkości (0,0,0)
ω3=(-√2/2,-√2/2,0)=ω4
Wzór (2) nie działa teraz gdyż wskazane przez niego ω=(-√2/2,0,0) nie pasuje do do wektorów prędkości. Jest dwukrotnie za mała. Wzór (2) można jedynie stosować do punktów znajdujących się na jednej osi.
Jak więc w tym przypadku uzyskać wspólną omegę dla wszystkich punktów?
Załóżmy że omega dla punktów m1, m2 jest to ωx` a dla punktów m3, m4 jest to ωy`. Sumując omegi dla tych osi uzyskujemy
ω=ωx`+ ωy` =(0, -2, 0) (3)
Otrzymujemy niejako średnią prędkość kątową. Pamiętając wzór że v = ω x r i wiedząc że r to składowa prostopadła do ω, czyli w tym przypadku współrzędna y obu punktów możemy policzyć v dal tych punktów. Okazuje się że są to dla punktów m1, m2, m3, m4 dostajemy odpowiednio v1, v2, v3, v4.
Przy takiej konfiguracji wszystko się zgadza a co jak weźmiemy nieco inną konfiguracje? Najpierw ustalmy pierwotną ωp
ωp=(1,0,0)
Niech omega będzie nachylona do jednej z osi o kąt inny niż 45 stopni, dobieramy łatwe do wyliczenia współrzędne punktów
m1 (4, 3, 0)
m2 (-4, -3, 0)
m3 (-3, 4, 0)
m4 (3, -4, 0)
Rozpatrujemy układ w którym spoczywa środek ciężkości BS vc=0. Ponieważ jest to bryła sztywna dlatego wektory prędkości poszczególnych punktów wyliczamy ze wzoru v = ω x r ale tym razem r jest prostopadłe do omegi czyli jest to pozycja y punktów.
v1=(0, 0, -3)=3
v2=(0, 0, 3)=3
v3=(0, 0, -4)=4
v4=(0, 0, 4)=4
Teraz wyznaczymy prędkość kątową osobno dla par m1,m2 i dla m3,m4. Tym razem r dla wszystkich punktów jest to wektor wodzący od środka układu i jego wartość to r1=r2=r3=r4=5.
1/r1=(3/25, 4/25, 0)
Mamy wtedy prędkości kątowe
ω1=ω2 ma kierunku(3, -4, 0) podstawiając do wzoru (1) mamy
ω1=(9/25, -12/25, 0)=ω2
prędkości kątowe ω3=ω4 ma kierunku(4, 3, 0)
ω3=(16/25, 12/25, 0)=ω4
Podstawiamy teraz ω12=ωx` ,ω34=ωy`do wzoru (3) i otrzymujemy omegę końcową
ωk=(25/25, 0, 0)
ωk=ωp
Wygląda na to że wzory (1) i metoda (3) są skuteczne dla takiej konfiguracji BS. Jednak wyliczając omegę średnią z dowolnych punktów wynik nie zawsze będzie prawidłowy. Trzeba by było przebadać metodę w różnych konfiguracjach i udowodnić kiedy można ją stosować a kiedy ona nie działa. Do tego co chcę zrobić jest ona wystarczająca, potrafię teraz w łatwy sposób wyznaczyć wektor chwilowej prędkości kątowej co jest dużym krokiem do przodu w stworzeniu mojej finalnej symulacji mechaniki punktów obracającej się bryły sztywnej.
Na koniec przyjrzyjmy się jeszcze schematowi pierwszemu, gdzie omega jest nachylona do osi głównych pod kątem 45 stopni. Jak wiemy BS jest zbiorem punktów powiązanych ze sobą siłą więzów.
Przyczyną zmiany wektora prędkości podczas ruchu krzywoliniowego jest przyspieszenie dośrodkowe
ad=(dv/dt)
Kierując wszystkie przyspieszenia do środka ciężkości zobaczymy że przyspieszenia każdą parą punktów się zerują. Przyspieszenia prostopadłe do omegi skutkują ruchem obrotowym a równoległe do siebie wzajemnie się neutralizują.
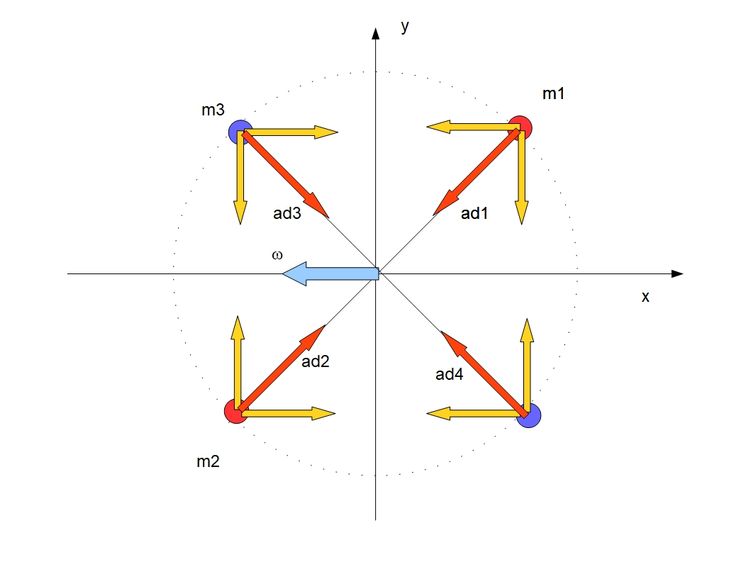
Jednak przyspieszenie jest skutkiem działania siły
a=F/m
F=ma
Kiedy przyjmiemy że wszystkie masy w schemacie są równe, to siły więzów między punktami również się zerują. Robi się ciekawie kiedy punkty na jednej osi mają inną masę niż punkty na osi prostopadłej.
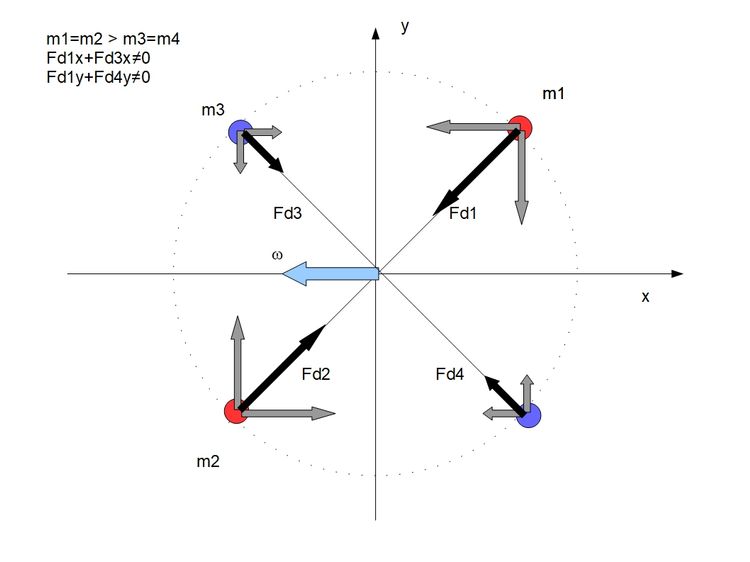
Zauważmy że m1, m2 dążą do obrotu wokół ω12 a masy m3,m4 chcą się kręcić wokół ω34. Jeżeli teraz zsumujemy siły między punktami do siebie prostopadłymi to okaże się że one się nie zerują. Jak pokazały to moje symulacje z tensorem bezwładności wypadkowa tych sił jest prostopadła do wektora krętu.
Znając wzór na zmianę wektora krętu dL= M = r x F siła ta dla krętu jest nieskuteczna i nie skutkuje zmianą wektora krętu w czasie. Wszystko się powoli zakleszcza i nawzajem pozytywnie weryfikuje i co najważniejsze nie ma tu żadnych sprzeczności z obecnym stanem wiedzy, a jedynie intuicyjne i szczątkowe szacunki nie uwzględniające detali zagadnienia skutkują błędną opiniom, że moje pomysły są z obecnym staniem nauki sprzeczne.
Zapowiada się na to że znów będę musiał zmienić miejsce pracy. Leprze warunki ale praca w delegacji w obcym dla mnie mieście. W moich poszukiwaniach jestem już blisko ale wciąż jeszcze dużo pracy do końca. Niestety znów będę musiał przerwać moje rozważania na kilka tygodni w celu aklimatyzacji w nowym miejscu, jeżeli dojdzie ono do skutku.
Inne tematy w dziale Technologie

