Przez chyba już półtora roku (najpierw na blogu profesora Jadczyka, potem już samotnie), kroczek po kroczku wgryzam się w tajemnicę mechaniki bryły sztywnej. Z uporem maniaka wałkuje ten temat tak długo (Jadczyk zresztą też), że większość ma już serdecznie dość tego tematu. Jednak ja uparcie poznaje kolejne szczegóły, które już teraz pozwalają lepiej i dokładniej opisać niektóre zagadnienia (np. poldhodia, herpolhodia) aniżeli jest to opisane w podręcznikach lub pokazać niektóre szczegóły o których nikt nie ma zielonego pojęcia (np. przyspieszenia kątowe).
Przeciwnik został otoczony i pozostała jedynie jedna tajemnica do odgadnięcia, jak podczas mechaniki obrotu BS działają siły więzów. Bogaty w wiedzę i doświadczenia rozpoczynam ostatni już etap wgryzania się w tą tajemnice.
Mam kilka wersji jak te siły mogą działać. Na starcie chciałem sprawdzić obecną interpretacje która wydawała mi się błędna, a tu niespodzianka i wyznaczone na ich podstawie momenty sił po porównaniu ze wzorami Eulera okazały się tożsame. Być może tyle szukałem aby ostatecznie potwierdzić poprawność obecnych założeń (takie życie), ale przy okazji pokazuje wiele szczegółów które wcześniej były nieznane.
Interpretacje sił więzów (które też są zwane siłami dośrodkowymi) w podręcznikach nie są jednoznaczne. I tak na przykład uważa się z jednej strony że siły te są centralne czyli skierowane są zawsze do środka ciężkości, z drugiej strony uważa się że są one zawsze prostopadłe do wektora omegi, czyli również chwilowej osi obrotu. Niestety rozpatrując mechanikę punktu interpretacje te są względem siebie sprzeczne, gdyż siła dośrodkowa skierowana prostopadle do osi obrotu rzadko kiedy jest siłą centralną.
Należy więc zadać pytanie, jak wygląda siła więzów działająca na punkt bryły sztywnej w następującej sytuacji?
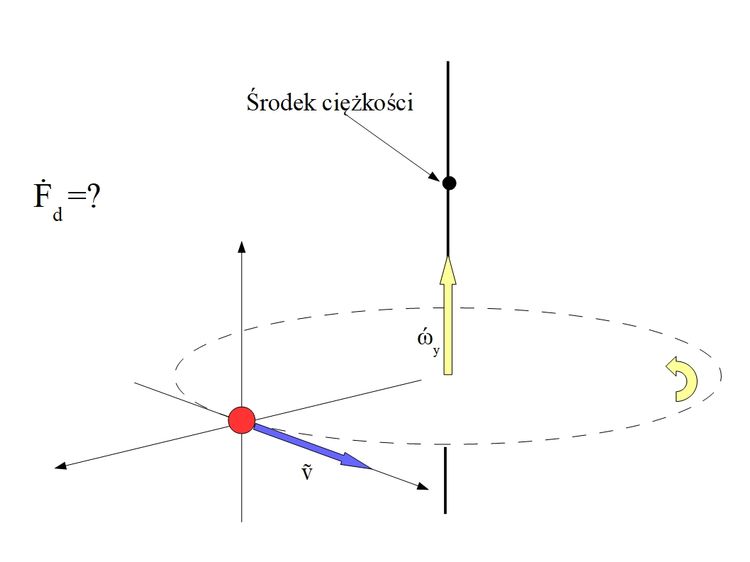
Ponieważ wielu oponentów, udaje że w podręcznikach nie ma zapisku że siły więzów są siłami centralnymi i twierdzą oni że siła ta jest zawsze prostopadła do omegi, to niejako z szacunku do nich od takiej wersji trzeba zacząć weryfikacje.
Wzór na siłę dośrodkową to
F
d=-m
ω2r (1)
Gdzie r jest wektorem. Oznacza to że Fd leży na kierunku r, a minus oznacza że ma przeciwny zwrot. Rozpatrujemy sytuację gdzie siła więzów jest prostopadła do ω czyli musimy wziąć r do niej prostopadły. Jeżeli ω ma jedynie składową (x, 0, 0) i założymy że v ma jedynie składową (0, 0, z) to wtedy do wzoru musimy podstawić składową promienia na osi y, czyli zerujemy inne składowe wektora położenia r (0, y, 0).
Bierzemy teraz jakiś model bryły sztywnej i przy powyższych założeniach, stosując wzór na siłę dośrodkową i kierując je prostopadle do osi obrotu, wychodzi taki przykładowy schemat.
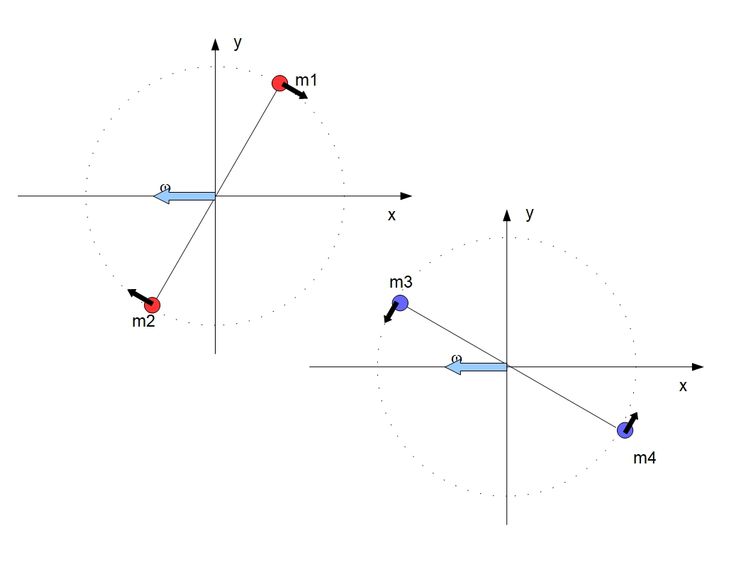
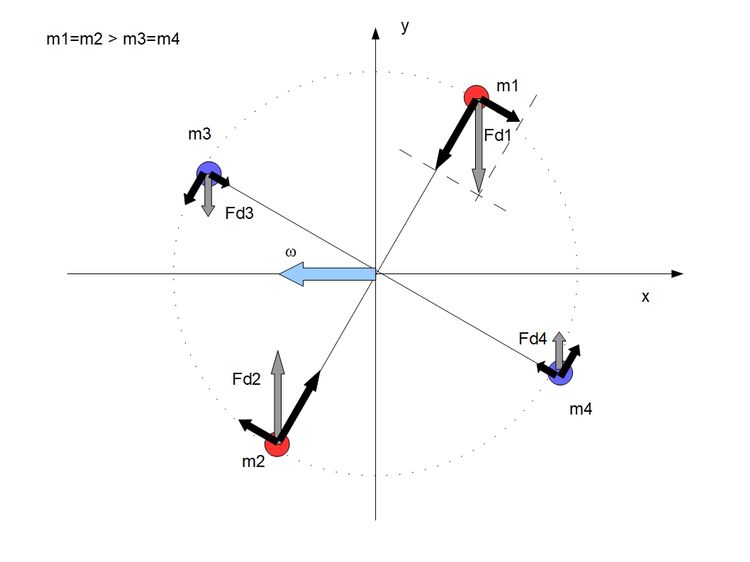
Jak widać takie umieszczenie sił generuje pewne problemy. Składowe tych sił które są zwrócone do środka się zerują, ale składowe do nich prostopadłe dają momenty sił które na osiach głównych się sumują. Znając zależności geometryczne jest to tym razem Fdrazy cosinus kąta nachylenia osi do wektora ω. Mamy więc wzór na składową centralną siły więzów
Fdc= Fdsinα (2)
oraz składową do niej prostopadłą dającą moment siły
Fdm= Fdcosα (3)
Teraz biorę wzory Eulera aby zweryfikować tą interpretację.
Zbyt długo aby tłumaczyć ale korzystam z następującego uproszczenia które wiem że jest poprawne. Płaski obiekt znajduje się na płaszczyźnie XY, na tej samej płaszczyźnie znajduje się wektor prędkości kątowej ω, co skutkuje tym że wektor momentu pędu również znajduje się na tej płaszczyźnie. Taki układ jest bardzo wygodny do obliczeń chwilowych wartości poszczególnych wektorów.
Do wzorów Eulera musimy przejść do układu odniesienia bryły, gdzie masy znajdują się na osiach głównych. O ile w symulacji nieruchomy jest wektor ω a to obiekt jest względem niego obracany, to podczas obliczeń dla Eulera jest dokładnie odwrotnie, to punkty są nieruchome a pozycje zmienia ω. Oznacza to że ω w moim wygodnym układzie odniesienia może mieć jedynie dwie składowe ω(x,y,0). Korzyści? Tylko jedno z trzech równań Eulera jest niezerowe
Iz(ωz/dt) + (Iy-Ix)ωyωx= 0 (4)
Przypomnę moją interpretacje tego wzoru
I(ω/dt) = Iɛ = M (5)
M - moment siły
Daje nam to
Mz= Ixωyωx – Iyωyωx (6)
Jak widać efektem jest moment siły na osi z, tak samo jak moment siły wynikający ze składowej siły więzów wzór Fdm (3).
Spodziewałem się porażki tej metody a tu w pełni zgodna pozytywna weryfikacja. Przy takich samych masach i długościach wektora r stosując wzór (3) zawsze wszystkie siły się zerują. Kiedy ustaliłem różne momenty bezwładności na osiach głównych, okazało się że masy na osi x` dają identyczne M jak człon Ixωyωxze wzorów Eulera, a masy na osi y` identyczne M jak człon Iyωyωx.
Poniżej zostawiam kod do symulacji w Vpython. Można w nim zmieniać dowolnie masy punktów, długości ramion oraz długość wektora omegi. Po włączeniu symulacji ukaże się animacja sił dośrodkowych metodą opisaną powyżej, z rozkładem tych sił na składowe centralne i do nich prostopadłe, w drugim oknie pokażą się wyniki obliczeń dla liczone metodą (3) i (6), można sobie sprawdzić że zawsze wartości są identyczne.
Dlaczego tak się dzieje pokazują nam zależności geometryczne. Podstawiając (1) do wzoru (3) otrzymujemy
Fdm= -mω2rycosα
Licząc moment siły z Fdm otrzymamy
M = -mω2ry(cosαr) = -mω2ryrx= -mω2r2cosαsinα
Natomiast składowe wzorów Eulera (6) to
M = -Iωyωx= -mr2ω2 cosαsinα
Po prostu licząc metodą (3) to wektor ω jest nieruchomy a licząc metodą (6) nieruchomy jest wektor r.
Życie często płata figle, chciałem obalić argumenty oponentów i potwierdzić wersje podręcznikową, że siły więzów są siłami centralnymi a wyszło na odwrót. Jest duża doza prawdopodobieństwa że to moi oponenci mieli racje, a podręczniki i ja się myliliśmy. Chciałem wyeliminować w pierwszej kolejności najsłabszą w mojej opinii wersje, a tu okazało się że jest ona teraz najbardziej prawdopodobnym rozwiązaniem. Z tym że moi oponenci wierzą w poprawność swojej interpretacji ale nie umieją jej uargumentować, a ja już posiadam solidne argumenty potwierdzające ich intuicje. Zapewne wielu dalej będzie zaprzeczać uzyskanym przeze mnie wynikom ale prawda jest taka że nie umieją oni przedstawić nic lepszego. Argumentacja sceptyków jest dość prymitywna: nie bo mi się to nie podoba i basta. A ja idę dalej i wiem coraz więcej.
Zapewne wielu by takim wynikiem się zadowoliło ale ja nadal ma sporo pytań, na które dalej szukam odpowiedzi. Skąd biorą się akurat takie siły więzów a nie inne? Czy uzyskane wyniki są zgodne z rzeczywistością? I pozostaje jeszcze zweryfikować pozostałe dwie metody. Będzie ciekawie jak któraś z nich również będzie skuteczna.
from visual import *
mx=1.5 #masy x`,y`
my=0.3
#pozycja musi byc liczba z kropka, np. 1. 4. 3.56
x1=1. #pozycja m1,m2 na osi x`
y2=2. #pozycja m3,m4 na osi y`
wx=0.9 #omega wzpolrzedna tylko x z kropka na 2.
################################################
#ponizej nie zmieniac
W=vector(wx,0,0)
y1=0
z1=0
x2=0
z2=0
n1=x1*x1
n2=y2*y2
k1=x1/10
k2=y2/10
Fdx=mx*W.x*W.x*y1 #sily dosrodkowe na osiach glownych z Fd=mW^2ry
Fdy=my*W.x*W.x*y2
#print "F", Fd1,Fd2
omega=arrow(axis=vector(W.x,W.y,0), color= color.blue, shaftwidth=0.05) #omega startowa
masa1x=sphere(pos=vector(x1,y1,0),radius=0.05) #bryla sztywna
masa2x=sphere(pos=vector(-x1,-y1,0),radius=0.05)
masa1y=sphere(pos=vector(x2,y2,0),radius=0.05)
masa2y=sphere(pos=vector(-x2,-y2,0),radius=0.05)
promien1=arrow(pos=masa2x.pos, axis=masa1x.pos-masa2x.pos, color= color.yellow, shaftwidth=0.005)
promien2=arrow(pos=masa2y.pos, axis=masa1y.pos-masa2y.pos, color= color.yellow, shaftwidth=0.005)
sila1=arrow(pos=masa1x.pos,axis=-vector(x1,y1,0)*Fdx, color= vector(1,1,0), shaftwidth=0.05) #wektory sil dosrodkowych punktow
sila2=arrow(pos=masa1x.pos,axis=-vector(-x1,-y1,0)*Fdx, color= vector(1,1,0), shaftwidth=0.05)
sila3=arrow(pos=masa1y.pos,axis=-vector(x2,y2,0)*Fdy, color= vector(1,1,0), shaftwidth=0.05)
sila4=arrow(pos=masa1y.pos,axis=-vector(-x2,-y2,0)*Fdy, color= vector(1,1,0), shaftwidth=0.05)
sila1sin=arrow(pos=masa1x.pos,axis=-vector(x1,y1,0)*Fdx, color= vector(1,1,1), shaftwidth=0.05) #wektory sil dosrodkowych punktow
sila1cos=arrow(pos=masa1x.pos,axis=-vector(x1,y1,0)*Fdx, color= vector(1,0.6,0), shaftwidth=0.05) #wektory sil dosrodkowych punktow
sila2sin=arrow(pos=masa1x.pos,axis=-vector(x1,y1,0)*Fdx, color= vector(1,0.3,0), shaftwidth=0.05) #wektory sil dosrodkowych punktow
sila2cos=arrow(pos=masa1x.pos,axis=-vector(x1,y1,0)*Fdx, color= vector(1,0.6,0), shaftwidth=0.05) #wektory sil dosrodkowych punktow
sila3sin=arrow(pos=masa1x.pos,axis=-vector(x1,y1,0)*Fdx, color= vector(1,0.3,0), shaftwidth=0.05) #wektory sil dosrodkowych punktow
sila3cos=arrow(pos=masa1x.pos,axis=-vector(x1,y1,0)*Fdx, color= vector(1,0.6,0), shaftwidth=0.05) #wektory sil dosrodkowych punktow
sila4sin=arrow(pos=masa1x.pos,axis=-vector(x1,y1,0)*Fdx, color= vector(1,0.3,0), shaftwidth=0.05) #wektory sil dosrodkowych punktow
sila4cos=arrow(pos=masa1x.pos,axis=-vector(x1,y1,0)*Fdx, color= vector(1,0.6,0), shaftwidth=0.05) #wektory sil dosrodkowych punktow
momentsx=arrow(axis=-vector(0,0.1,0), color= vector(0.,0.8,0.8), shaftwidth=0.05) #wektory sil dosrodkowych punktow
momentsy=arrow(axis=-vector(0,0.1,0), color= vector(0.,0.8,0.8), shaftwidth=0.05) #wektory sil dosrodkowych punktow
t=0
while t<20:
rate(3)
x1=x1-k1 #nowe pozycje punktow
y1=sqrt(n1-(x1*x1))
y2=y2-k2
x2=-sqrt(n2-(y2*y2))
r1=vector(x1,y1,0) #promienie
r2=vector(-x1,-y1,0)
r3=vector(x2,y2,0)
r4=vector(-x1,-y1,0)
# print mag(r1),mag(r2),mag(r3),mag(r4)
sina1=y1/mag(r1) #sin kata nachylenia dla x` i y`
cosa1=x1/mag(r1)
sina2=y2/mag(r3)
cosa2=x2/mag(r3)
# print t,sina1,cosa1, (sina1*sina1)+(cosa1*cosa1)
if y1<0: #wartosc sily dosrodkowe Fd=mW^2ry
Fdx=mx*W.x*W.x*y1
else:
Fdx=-mx*W.x*W.x*y1
if y2<0:
Fdy=my*W.x*W.x*y2
else:
Fdy=-my*W.x*W.x*y2
Fd1=vector(x1,y1,0)*Fdx #wektory sil dosrodkowch z Fd=mW^2ry
Fd2=vector(-x1,-y1,0)*Fdx
Fd3=vector(x2,y2,0)*Fdy
Fd4=vector(-x2,-y2,0)*Fdy
Mx=vector(0,0,Fdx*cosa1*mag(r1)) # M = Fdcosa x r
My=vector(0,0,Fdy*cosa2*mag(r3))
Ix=mx*mag(r1)*mag(r1) #momenty bezwladnosci
Iy=my*mag(r3)*mag(r3)
MzIxwxwy=-Ix*(W.x*sina1)*(W.x*cosa1) #Euler Iz(dwz/dt)=Ixwxwy-Iywxwy
MzIywxwy=Iy*(W.x*sina1)*(W.x*cosa1)
print t, "Mz = r x cosFdx ", Mx, " Mz Euler Ixwxwy", MzIxwxwy
print " Mz = r x cosFdy", My, " Mz Euler Iywxwy", MzIywxwy
masa1x.pos=vector(x1,y1,0)
masa2x.pos=vector(-x1,-y1,0)
masa1y.pos=vector(x2,y2,0)
masa2y.pos=vector(-x2,-y2,0)
promien1.pos=masa2x.pos
promien1.axis=masa1x.pos-masa2x.pos
promien2.pos=masa2y.pos
promien2.axis=masa1y.pos-masa2y.pos
sila1.pos=vector(x1,y1,0)
sila1.axis=vector(0,-mag(Fd1),0)
sila2.pos=vector(-x1,-y1,0)
sila2.axis=vector(0,mag(Fd2),0)
sila3.pos=vector(x2,y2,0)
sila4.pos=vector(-x2,-y2,0)
if t<10:
sila3.axis=vector(0,-mag(Fd3),0)
sila4.axis=vector(0,mag(Fd4),0)
else:
sila3.axis=vector(0,mag(Fd3),0)
sila4.axis=vector(0,-mag(Fd4),0)
sila1sin.pos=vector(x1,y1,0)
sila1sin.axis=-vector(x1,y1,0)*mag(Fd1)*sina1/mag(r1)
sila1cos.pos=vector(x1,y1,0)
sila1cos.axis=vector(y1,-x1,0)*mag(Fd1)*cosa1/mag(r1)
sila2sin.pos=vector(-x1,-y1,0)
sila2sin.axis=-vector(-x1,-y1,0)*mag(Fd2)*sina1/mag(r2)
sila2cos.pos=vector(-x1,-y1,0)
sila2cos.axis=vector(-y1,x1,0)*mag(Fd2)*cosa1/mag(r2)
if t<10:
sila3sin.pos=vector(x2,y2,0)
sila3sin.axis=-vector(x2,y2,0)*mag(Fd3)*sina2/mag(r3)
sila3cos.pos=vector(x2,y2,0)
sila3cos.axis=vector(y2,-x2,0)*mag(Fd3)*cosa2/mag(r3)
sila4sin.pos=-vector(x2,y2,0)
sila4sin.axis=vector(x2,y2,0)*mag(Fd4)*sina2/mag(r4)
sila4cos.pos=-vector(x2,y2,0)
sila4cos.axis=vector(-y2,x2,0)*mag(Fd4)*cosa2/mag(r4)
else:
sila3sin.pos=vector(x2,y2,0)
sila3sin.axis=vector(x2,y2,0)*mag(Fd3)*sina2/mag(r3)
sila3cos.pos=vector(x2,y2,0)
sila3cos.axis=-vector(y2,-x2,0)*mag(Fd3)*cosa2/mag(r3)
sila4sin.pos=-vector(x2,y2,0)
sila4sin.axis=-vector(x2,y2,0)*mag(Fd4)*sina2/mag(r4)
sila4cos.pos=-vector(x2,y2,0)
sila4cos.axis=-vector(-y2,x2,0)*mag(Fd4)*cosa2/mag(r4)
momentsx.axis=vector(0,0,2*Mx.z)
momentsy.axis=vector(0,0,2*My.z)
t=t+1
Inne tematy w dziale Technologie

