Niniejszy poprawnie działający algorytm jest kolejnym dowodem na poprawność moich założeń, dotyczących zależności wektorowych podczas mechaniki obrotu bryły sztywnej. Stosowana w moich symulacjach metoda krokowa, jest uważana przez wielu za bardzo prymitywną i toporną.
W skrócie metodę krokową można opisać jako:
1a wyliczenie na podstawie parametrów konkretnej chwili, zmian w jakimś odcinku czasu dt,
1b następnie zastosowanie tych zmian, czyli wyliczenie parametrów po upływie odcinka czasu dt,
2a na podstawie nowo uzyskanych parametrów, ponownie wyliczamy zmiany w kolejnym odcinku czasu dt.
2b itd. …
Dlaczego nikt nie lubi tej metody? Gdyż jest ona bardzo wymagająca i każdy nawet najmniejszy błąd przyrasta z każdym krokiem. A ponieważ w większości przypadkach trzeba zastosować jakąś formę zaokrągleń wyników, dlatego też w większości przypadków niemożliwe jest uzyskanie pełnej dokładności wyniku. Jednak możliwe jest uzyskanie błędu na tyle małego że nie wpływa on znacząco na wynik końcowy i można go pominąć. Ale aby uzyskać tak mały błąd w tej metodzie, niezbędne jest dokładne odwzorowanie każdego szczegółu. Pominięcie nawet najmniejszego detalu skutkuje narastaniem błędu który jest jego skutkiem. Dlatego tez stosuję tą metodę gdyż pokazuje każdy błąd i to właśnie ostatnim czasy mi się przytrafiło.
Moje wcześniejsze symulacje potwierdzały moje przypuszczenia, dokładnie wiem jak te symulacje działają i znam skutki tych działań. Jednym z głównych celów moich poszukiwań jest uzyskanie możliwie najkrótszego algorytmu pozwalającego symulować mechanikę obrotu BS. Już jakiś czas temu powstały pierwsze kody które „prawie” działały, ale prawie robi wielką różnice. Uzyskiwane wyniki były dalekie od moich oczekiwań. Byłem prawie pewny że mam racje ale występowały dość duże błędy, jak przyrost wektora krętu o 10% przy tysiącach kroków i jego nieznaczny ale zmieniający się kierunek o kilka stopni. Ostatnie trzy tygodnie szukałem co robię źle analizując różnice w pojedynczych krokach.
Chociaż w teorii algorytm jest bardzo prosty to jednak wymaga użycia tensora momentu bezwładności I, a jego wyliczenie to sumowanie dziewięciu równań (od trzech do pięciu operacji matematycznych na równanie) dla każdego punktu BS. Potrzebne jest też zastosowanie I^-1 odwrotność macierzy tensora. Wyznaczenie samego wyznacznika tej macierzy to 18 operacji matematycznych na dziewięciu elementach. Wyliczanie tej macierzy to kolejne kilkadziesiąt działań matematycznych, gdzie pomylenie plusa z minusem, czy pomylenie któregoś z elementów, lub podmiana ich kolejności skutkuje błędnym wynikiem. Samo sprawdzanie poprawności zapisu zajęło mi wiele godzin. Wszystko było sprawdzone na kilka sposobów, a algorytm dalej nie działał tak jak trzeba. Problem był przy przyspieszeniu kątowym ɛ. Ponieważ mam już działające symulacje mogłem porównać pierwsze kroki. Cały czas okazywało się że współrzędne ɛ w pierwszym kroku są o kilka tysięcznych inne od oczekiwanych. Ten niewielki błąd zmieniał nieznacznie kierunek działania tego wektora ale to wystarczało by generować dość duży błąd. Być może zła kolejność działania, być może gdzieś błąd algorytmie? Okazało się że przegapiłem że wektor ɛ obraca się wraz z BS. Po wprowadzeniu jednej linijki kodu korygującą pozycje ɛ o rotacje BS rozwiązało problem. Wyniki są bardziej niż zadowalające.
Po tym dość długim wstępie, matematyczny zapis algorytmu. Równania Eulera wyprowadzane są z równania
I(dω /dt) + ω x Iω = Mzew (1)
Gdzie
I - tensor momentu bezwładności
Mzew - moment sił zewnętrznych, podczas swobodnego obrotu równy zero
wiedząc że:
M=Iɛ (2)
ɛ=dω /dt (3)
L= Iω (4)
Zakładając że Mzew=0, otrzymujemy taką zależność
I(dω /dt) = Iω x ω (5)
Wykorzystując teraz zależności (2) (3) (4) uzyskujemy bardo proste równanie
M = L x ω (6)
oraz
ɛ=M*I^-1 (7)
Mój algorytm wykorzystuje równanie (6) do wyliczenia momentu sił wewnętrznych M. Następnie obracam BS i co bardzo ważne wektor M, wzdłuż prędkości kątowej ω, o odcinek czasu dt. Następnym działaniem jest wyliczenie ɛ z równania (7) i zmianę wektora ω zgodnie ze wzorem (3). Jest to jeden pełny krok po której mamy nową pozycje BS i inną pozycje wektora ω i na podstawie tych parametrów wyliczamy kolejny krok.
Bardzo proste działanie. Wielu zarzuca niesłusznie że nie mogą istnieć Momenty sił wewnętrznych, gdyż musiały by one skutkować zmianą wektora krętu. Więc ostatecznie obalamy ten argument i wyrzucamy go definitywnie do kosza, sprawdzając co się dzieje z wektorem L podczas działania momentu siły ze wzoru (6).
Tak jak pisałem wcześniej używając tej metody błędy będą zawsze. Wektor krętu największą zmianę względem położenia pierwotnego uzyskuje gdy BS pochyla się o 90 stopni następnie ten błąd się zmniejsza. Ile wynosi ten błąd?
Dla wektorów startowych L(0, 2, 0.3), ω(0, 1, 0.1) przy:
-dt=0,01 i po 1000 kroków (mniej więcej jedno fiknięcie) długość wektora zmieniła się w przybliżeniu o 0,006 a współrzędne x,y,z zmieniły swoje pozycje mniej więcej o 0,003.
-dt=0,005 i po 2000 kroków, długość wektora L zmieniła się o 0,003 a współrzędne x,y,z zmieniły swoje pozycje o niecałe 0,002
-dt=0,001 i po 10tyś kroków, długość wektora L zmieniła się o 0,0005 a współrzędne x,y,z zmieniły swoje pozycje o niecałe 0,004.
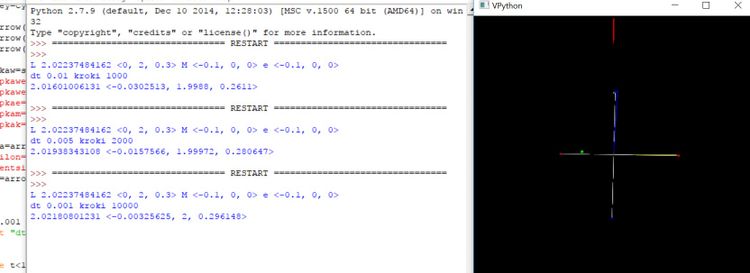
Może napisze słownie, przy dziesięciu tysiącach kroków mamy błąd rzędu 10^-4. Czyli Mimo że przez całą symulację działa moment siły, to na podstawie tych wyników można przyjąć że nie skutkuje on zmianą wektora Krętu. Każdy kto twierdzi że podczas obrotu BS nie występują momenty sił i nie ma tam przyspieszeń kątowych, po prostu się myli. Pomylić się jest rzeczą ludzką ale tkwić na upartego w błędzie jest głupotą i grzechem, dla naukowca najcięższym!
Dlaczego tak się dzieje? Tego jeszcze nie wiem ale mam zamiar się dowiedzieć. Na razie wiem że ten moment siły z równania (6) jest prostopadły do wektora krętu. Wynika to chociażby z faktu że jest wynikiem iloczynu wektorowego, czyli musi być prostopadły, ale łatwo jest to też wyliczyć za pomocą iloczynu skalarnego L na M.
Algorytm podam wkrótce gdyż muszę go trochę przygotować, ponieważ jest w nim pełno śmieci po różnych próbach które trzeba usunąć a dzisiaj jest już na to za puźno.
Inne tematy w dziale Technologie

