Niestety wkradł się błąd wczoraj wieczorem miałem stanąłem przed takim problemem jak odjąć wektory A_ i B_ w takiej sytuacji
A_ - B_(1/x) no i się zakręciłem i zrobiłem to źle. Już poprawiłem a pomyłka nie miała wpływu na wynik końcowy.
Doskonale zdaje sobie sprawę że moje zapisy tutaj na salonie24 są dalekie od ideału. Nie ma ty możliwości formatowania wzorów matematycznych ale postaram się od teraz robić to lepiej.
Kontynuuje odpowiedź na pytania które zadałem dość dawno temu, jak działają siły więzów podczas obrotu ciał sztywnych? Na pytania te nikt nie umiał odpowiedzieć, więc musiałem wykonać sporo pracy aby za pomocą dedukcji zdobyć umiejętności i wiedze pozwalające odpowiedzieć mi na te pytania. Tym blogiem jednocześnie sprawdzam czy moje wnioski są poprawne i jak do tej pory wszelkie próby weryfikacji są pozytywne.
Mamy więc trzy sytuacje
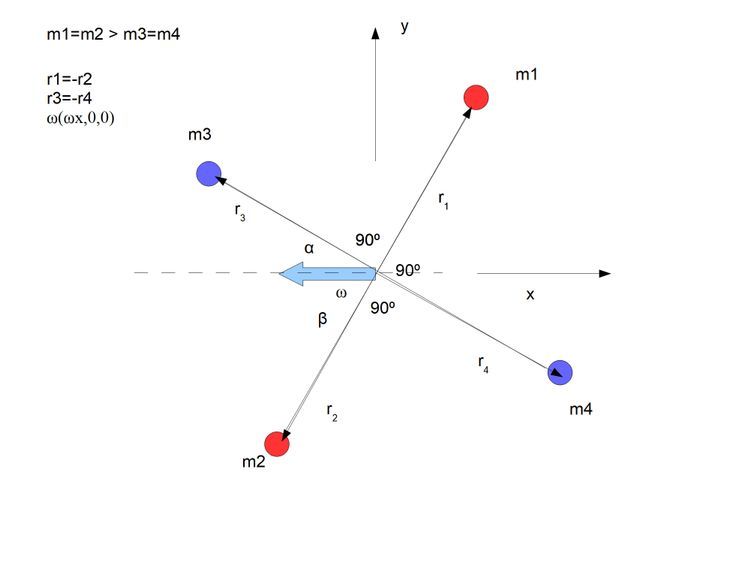
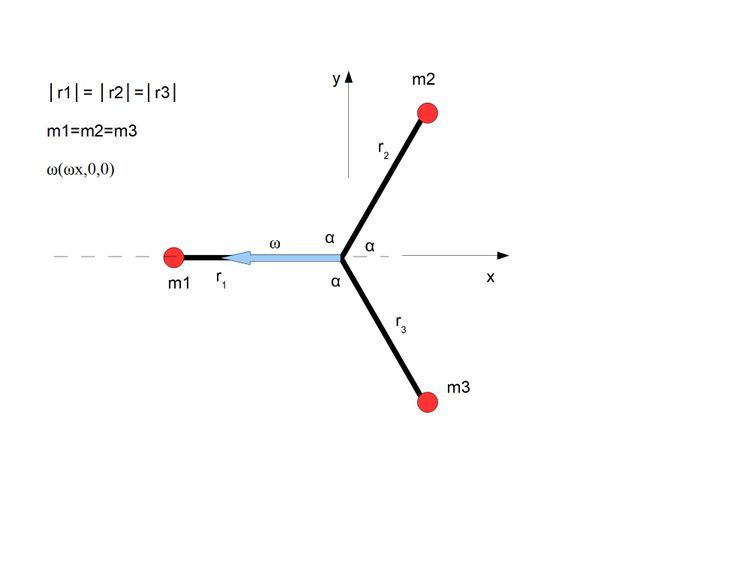
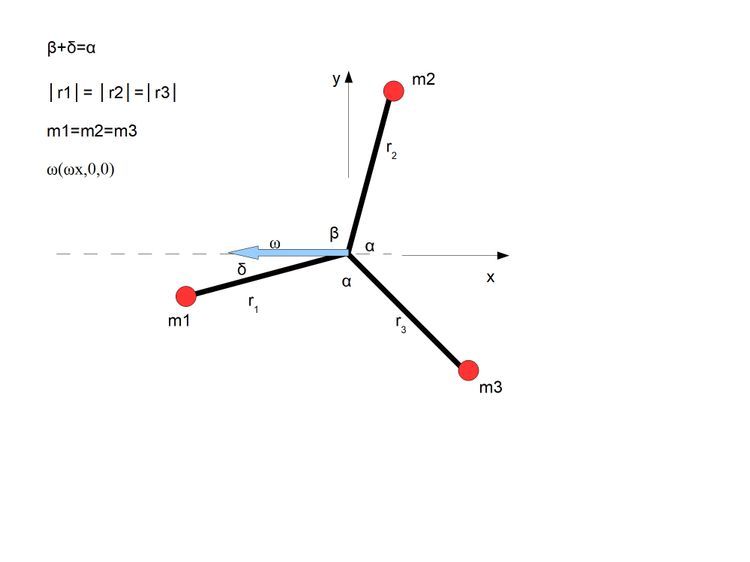
Mój sposób rozwiązania z opisem i szczegółami kalkulacji sytuacji pierwszej przedstawiłem na poprzednim blogu https://www.salon24.pl/u/przestrz/896396,kalkulacje-sil-wiezow-podczas-obrotu-cial-sztywnych
Jednak kalkulacje odbywały się na liczbach, więc udowodnię że wzory na siły więzów dla punktu m3 zawsze są prawdziwe już bez opisu. Mamy więc podany wektor prędkości kątowej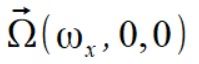 
oraz wektor położenia punktu m3 
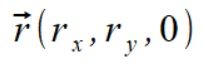. Liczymy najpierw wektor prędkości 
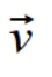ze wzoru prędkość liniową
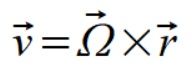(1)
prędkość liniowa punktu m3 to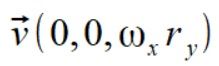 
, liczymy teraz prędkość kątową prostopadłą do wektora położenia używając wzoru
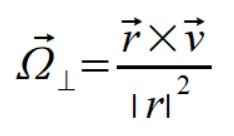(2)
definiuje odwrotność wektora jako ułamek wektora
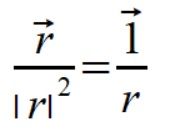
i zapisuje wzór (2) wygodniejszej dla mnie postaci
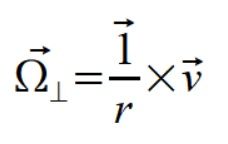(2a)
to daje nam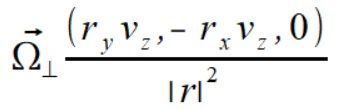 
i po użyciu współrzędnej vz daje nam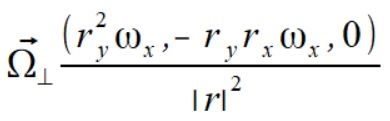 
Liczymy teraz składową prędkości kątowej równoległej do wektora położenia
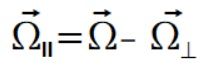(3)
daje nam to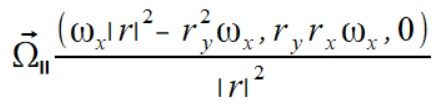 
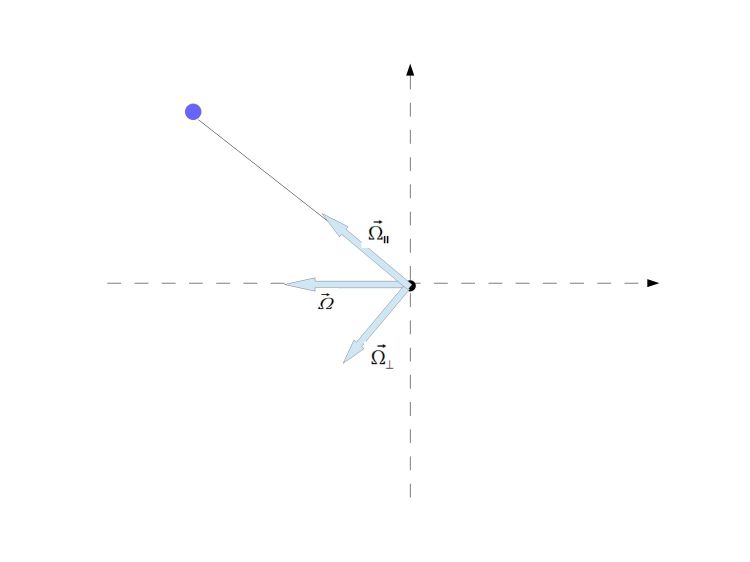
Wzór na przyspieszenie dośrodkowe
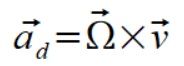(4)
liczymy teraz przyspieszenie centralne z prędkości kątowej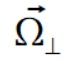 
prostopadłej do wektora położenia
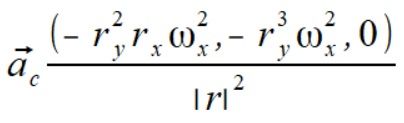
następnie liczymy przyspieszenie wynikające z prędkości kątowej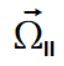
równoległej do wektora położenia
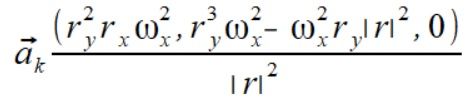
Po dodaniu wektorów przyspieszeń otrzymujemy wypadkową przyspieszenia dla punktu m3
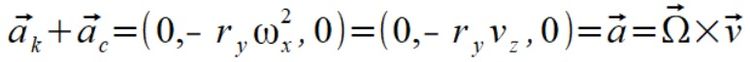
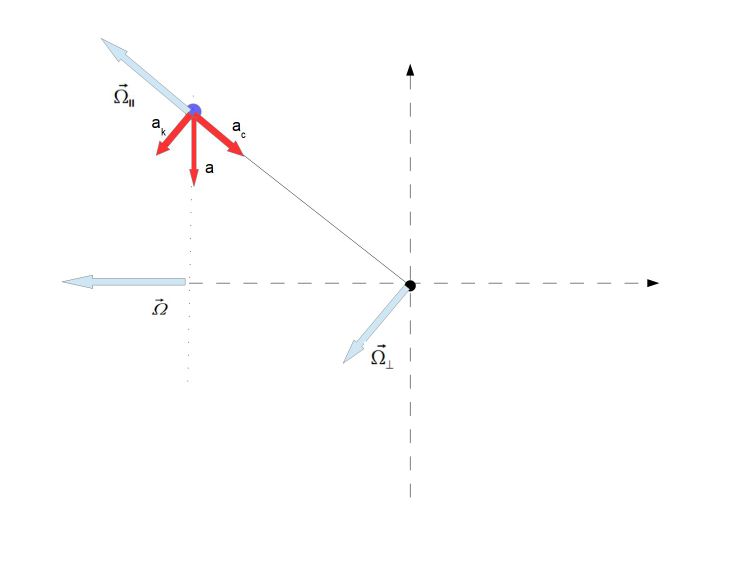
Wektory sił to pomnożenie wektorów przyspieszeń przez masę punktu m3
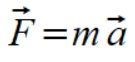(5)
Analogicznie liczymy wektory sił dla pozostałych punktów.
Niestety pisanie formuł jest pracochłonne dlatego na tym skończę tą notkę. Pozostaje odpowiedzieć jeszcze na dwa pozostałe schematy ale z tą wiedzą którą tutaj pokazałem nie jest to już trudne, chociaż aby uzyskać pełną odpowiedź czegoś jeszcze brakuje ale ten brak będzie jedynie pewną oczywistą oczywistością:)
