Z powodu zaistnienia dużej ilości osobistych problemów przez jakiś czas musiałem odpuścić, ale wygląda na to że w końcu wychodzę na prostą i postaram się dokończyć wyjaśnianie ostatnich tajemnic mechaniki bryły sztywnej. Z wyliczeń pozostaje jedynie udowodnić że, wewnętrzny moment siły który jest wynikiem moich wyliczeń wynika z prawa zachowania momentu pędu, a właściwie to go uzupełnić gdyż jakiś czas temu udało mi się pokazać jego zarys, ale jest on nie kompletny i jak do tej pory nikt go nie umiał poprawić ani obalić.
https://www.salon24.pl/u/przestrz/833687,wyprowadzenie-rownania-momentu-sily-wewnetrznych
Jest duży problem czym jest i jak liczyć zmianę tensora bezwładności dI/dt. W wolnym czasie wielokrotnie podchodziłem do tego problemu ale jak na razie ukrywa on przede mną swoje tajemnice. Zrozumienie tego zagadnienia wymaga sporo wolnego czasu i sporo rachunków, które często doprowadzają mnie do zagadnień matematycznych których nie umiem rozwiązać, ale cierpliwie kroczek po kroczku wgryzam się w temat, kropla drąży skałę.
Dzisiaj o energii punktu w czasie obrotu BS, czyli temat od którego powinno się zacząć rozważania a który pojawiał się u mnie bardzo rzadko. Niejako kończę tym czym powinienem zaczynać, ale z wiedzą jaką posiadłem będę mógł zobaczyć energie tego mechanizmu z zupełnie innej strony. Jest to notka rozpoznawcza, czyli sporo pytań na które jeszcze nie znam odpowiedzi, które dopiero postaram się je znaleźć.
Przypomnijmy prawo zachowania momentu pędu
"Moment pędu bryły pozostaje stały, gdy nie działa na nią żaden moment siły zewnętrznej."


Standardowy pokaz który pokazuje się w takich sytuacjach. Przyciągając ciężarki do siebie zmniejszamy moment bezwładności co skutkuje zwiększeniem prędkości kątowej, co opisuje poniższy wzór
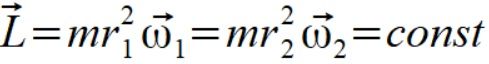 (3)
(3)
Mamy więc taką sytuacje
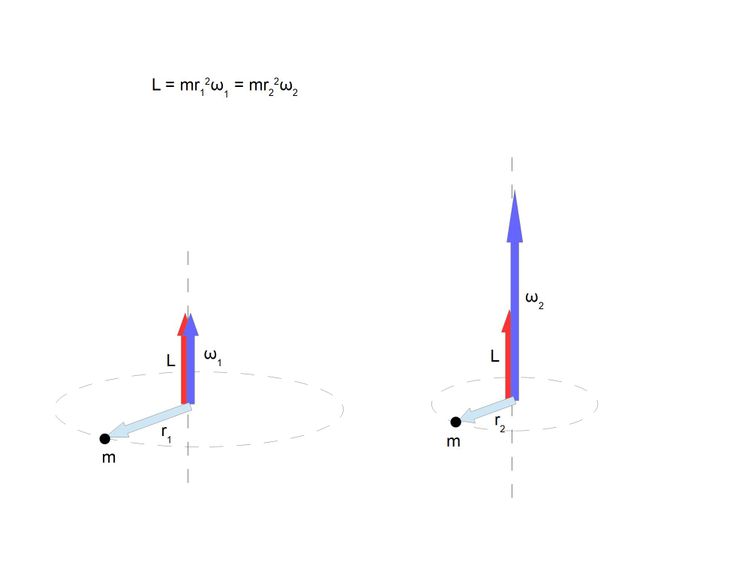
Zobaczmy więc co się dzieje z energią punktu o masie m. Aby było łatwiej zrozumieć liczę energie kinetyczną punktu z prędkości liniowej na liczbach.
m=3 jest stała w czasie
r1=4; r2=2; ω1=2 (4)
łatwo wyliczamy momenty bezwładności I=mr2
I1=48; I2=12
liczymy też moment pędu który jest stały w czasie wynosi (3)
L=I1ω1=96
liczymy prędkość kątową dla r2 (3)
ω2=L/I2=8
Jak widać zmniejszenie o połowę odległości od osi obrotu czterokrotnie zwiększyło prędkość kątową. Liczymy więc prędkość liniową punktu w obu przypadkach
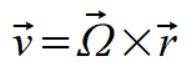 (5)
(5)
W naszym przypadku wszystkie trzy wektory są do siebie prostopadłe więc działa tu wzór
v=ωr
v1=8; v2=16
Energia kinetyczna punktu to
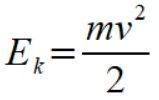 (6)
(6)
czyli dla naszych dwóch przypadków
Ek1=96; Ek2=384
Niefortunnie wartość momentu pędu ma tą samą wartość co jedna z naszych energii ale jest to tylko zbieg okoliczności. Najważniejszą obserwacją jest fakt że w tym konkretnym przypadku, skrócenie o połowę odległości od osi obrotu skutkuje czterokrotnym przyrostem energii kinetycznej. No ale skąd ten przyrost energii, czy zostaje tutaj złamane prawo zachowania energii?
Oczywiście nie łamiemy tutaj prawa zachowania energii i jest to naturalny stan dla ruchu obrotowego, analogiczną sytuacje mamy dla układów planetarnych wokół gwiazdy, im planeta znajdzie się bliżej gwiazdy tym większa posiada energie kinetyczną a wynika to z utraty energii potencjalnej. Jednak wydaje mi się że wszystkim unika pewien szczegół, albo jest on znany tylko nie opisuje się go w podręcznikach, że siła więzów na filmiku rozchodząca się przez ramiona obiektu kręconego (ale mogąca się rozchodzić na przykład przez sznurek), to nie do końca to samo co siła zachowawcza grawitacji która odpowiada za ruch obrotowy planet.
Czym jest siła zachowawcza? Mamy dwie definicje
"Siła zachowawcza – siła mająca tę własność, że praca wykonana przez nią przy przemieszczaniu ciała na drodze o początku A i końcu B zależy tylko od położenia punktów A i B, nie zależy zaś od przebiegu drogi, czyli od toru ruchu. "
"Siłami zachowawczymi są wszystkie siły centralne. Np. siłami centralnymi są siły grawitacyjne w klasycznej teorii grawitacji Newtona, siły kulombowskie oddziaływań między ciałami posiadającymi ładunki elektryczne. Także siły sprężystości ciał doskonale sprężystych są siłami centralnymi"
Znalazłem też ciekawy komentarz że "W ogólności siły z którymi mamy do czynienia (i które zazwyczaj się rozważa) mogą zależeć od położenia (obiektu na który działa dana siła), czasu, oraz prędkości (tego obiektu). Siły potencjalne są to siły, które mogą zależeć od położenia i czasu, ale nie zależą od prędkości. Natomiast siły zachowawcze to siły, które zależą tylko od położenia. Zatem każda siła zachowawcza jest potencjalna, ale nie każda siła potencjalna jest zachowawcza."
https://zapytajfizyka.fuw.edu.pl/pytania/jakie-sily-sa-potencjalne-lub-zachowawcze/
W przypadku ruchu obrotowego w przestrzeni kosmicznej sprawa jest oczywista to siła grawitacji przyciąga masy i jest ona odpowiedzialna za ruch obrotowy. Prawo powszechnego ciążenia opisują tą siłę i jest ona zależna jedynie od masy obiektów i odległości między nimi i występuje ona zawsze nie da się jej obejść. Aby oddalić od siebie dwa obiekty, zawsze potrzebujemy zużyć energie.
Jaka jest różnica między siłą grawitacji a naszym przypadkiem czyli silą więzów?
-Póki układ się nie obraca, oddalenie od siebie obiektów czyli niejako zwiększanie potencjału układu nie wymaga pokonania siły zachowawczej, gdyż ona wtedy nie działa. Siła centralna czyli siła więzów zaczyna dopiero działać kiedy układ zaczyna się obracać.
-Wielkość siły więzów nie zależy tylko od odległości ale jest też zależne od prędkości punktów. Przy tym samym promieniu możemy mieć różne prędkości kątowe czyli też różną wartość siły więzów.
-gdy już układ zacznie się obracać i jest on odizolowany, to przyrost energii kinetycznej jest ściśle powiązany ze zmianą obiektu względem osi obrotu, ale siła więzów przestaje działać po zerwaniu więzów.
Budzi to wiele moich pytań i wydaje mi się że być może mechanizmy te dadzą nowe możliwości. Czy w naszym przypadku siła więzów jest siłą zachowawczą, czy też nie jest? Skoro oddalając obiekty od siebie zyskujemy energie potencjalną to skąd ona jest pobierana? Przyciągając sznurek do siebie zyskujemy energie kinetyczną pokazały to moje wyliczenia, czyli została wykonana praca dodatnia ubyło energii potencjalnej, ale wydaje mi się że zwijanie sznurka wymaga zużycia energii, a nie na odwrót. Na czym polega różnica w ruchu obrotowym między siła grawitacji a siłą więzów?
Nie znam tych odpowiedzi ale postaram się je poznać, zapewne znów nie zabraknie takich którym te pytania się nie spodobają:)
Dla mnie ruch obrotowy to szczególny przypadek ruchu prostoliniowego na który działa prostopadła siła zwana też dośrodkową. Kiedy ta siła przestaje działać na ciało i nie działa żadna inna, to zacznie się ono poruszać ruchem jednostajnym prostoliniowym. To siła dośrodkowa jest przyczyną istnienia prędkości kątowej i kiedy jej zabraknie ruch obrotowy zanika, a ciało jest wystrzelone jak z procy sznurkowej.
Jak można by to wykorzystać?
Powiedzmy że wynieśliśmy w przestrzeń kosmiczną 1 tonowy obiekt. Owszem kosztowne ale przy obecnej technice nie stanowi wielkiego wyzwania. nasz obiekt składa się z dwóch modułów po 0,5 tony. Za pomocą sprężyny lub jakiegoś ładunku wybuchowego rozczepiamy moduły od siebie nadając im przeciwne prędkości, jednak są one dalej połączone liną powiedzmy 200m (100m to środka ciężkości). Kiedy lina się napnie musimy jakoś uniknąć odbiciu, tak by moduły się do siebie nie zbliżały. Teraz jakoś rozpędzić prędkość kątową, czy to używając żagli słonecznych czy też jakiś niewielkich rakiet. Aby rozpędzić 500kg do prędkości 100 m/s trzeba zaledwie 5M J (litr benzyny to to 23M J). W naszym przypadku wektory prędkości v, położenia r i momentu pędu L są do siebie prostopadłe, czyli zachowują się proporcje L=mrv. Masa jest stała, czyli zgodnie z prawem zachowania momentu pędu (3) zwinięcie liny do 2m czyli skrócenie ją stukrotnie, daje nam stukrotne zwiększenie prędkości v. Zrywamy line i mamy 500 kg moduł rozpędzony do 10 km/s, zyskaliśmy 50 000 000 000 J (najdalej wysłana ludzka sonda Voyager1 porusza się z prędkością 17 km/s).
Ten rozpędzony moduł może składać się z następnych dwóch, czyli możemy powtórzyć operacje dodając prędkość. Dzieląc nasz obiekt na pół, po dziewięciu razach mamy obiekt 2kg, po dziesięciu 1kg. Przy obecnej miniaturyzacji może się okazać że to już wystarczy by stworzyć użyteczną sondę o tak niewielkiej masie. Oczywiście jest wiele problemów do rozwiązania, jak może być największa wytrzymałość takiej liny, ogromne przeciążenia w czasie ruchu obrotowego z dużymi prędkościami może uszkodzić wiele elementów itp ale jest to kwestia techniczna. Teoretycznie nie ma ograniczenia zwiększania tej prędkości i wszystko zależy od wytrzymałości użytych materiałów.
Jednak pozostaje pytanie skąd się bierze ta energia? Teoretycznie zbliżając do siebie te moduły zamieniamy energie potencjalną na kinetyczną, czyli ubytek energii potencjalnej wykonuje prace. Ale muszę tu pogdybać bo jeszcze nie posiadam tej wiedzy i wydaje mi się że przybliżanie do siebie ciał będzie wymagało użycia energii, czyli będziemy musieli mieć tą energie na zwinięcie linki. Jednak można tu użyć silnika elektrycznego napędzane prądem z baterii słonecznych, a to już jest duża oszczędność w stosunku do obecnych technik rakietowych, które wymagają użycia energii zawartej w paliwie. Paliwo jest masywne, czyli na wyniesienie odpowiedniej ilości paliwa musimy poświęcić jeszcze więcej paliwa, baterie słoneczne też ważą ale w przeciwieństwie do paliwa nie zużywają się szybko i działając odpowiednio długo mogą wytworzyć potrzebną energie.
Innym moim pomysłem jest połączenie belką dwóch szczytów górskich o głębokiej dolinie. Niewielki pakunek jest połączony z belką długą liną i nadajemy mu prędkość kątową. Lina nawija się na belkę zmniejszając swoją odległość od osi obrotu.
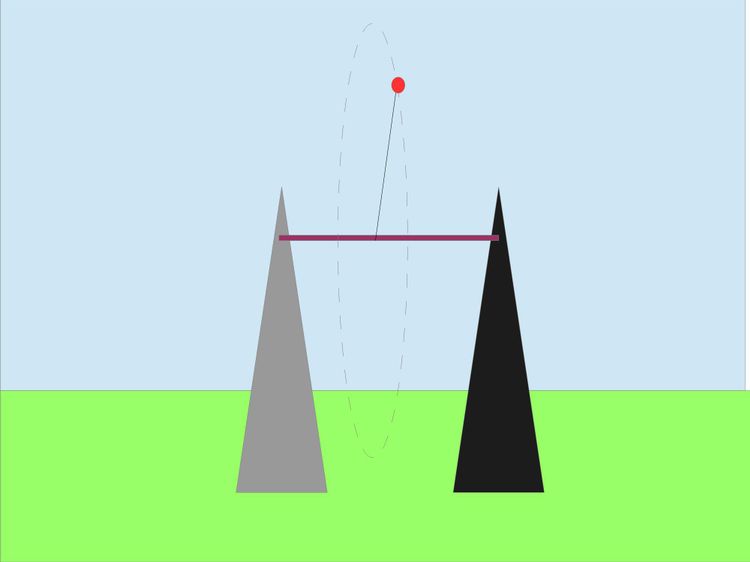
Zgodnie z prawem zachowania momentu pędu zwiększa się jej prędkość. Jeżeli lina była by odpowiednio długa i wytrzymała mogła by nadać pakunkowi wystarczająca prędkość aby go wyrzucić na orbitę. Przerywamy linę i wystrzeliwujemy pakunek.Pytanie jest z jaką precyzją udało by się taki ładunek wystrzelić, jak go potem odebrać i jakie elementy można tak wystrzeliwać, bo przeciążenia będą ogromne. Jednak wysłanie na orbitę polskiego satelity trochę ponad 2 kg kosztowało 135 tyś Euro, wydaje mi się że moja technika była by o wiele tańsza. Oczywiście wszystkiego w ten sposób wystrzelić się nie da, ale na przykład wodę czy jakieś śrubki, profile inne metalowe elementy które mogły by być składane na orbicie już tak.
Oczywiście jest to notka bardzo ogólna, wile pytań mało konkretów ale trzeba wrócić po dłuższej przerwie.








Komentarze
Pokaż komentarze (18)