Jak poprawić Newtona

Spis treści
1. Wstęp - Bawiąc się liczbami
2. Dlaczego "rozluźnienie" i "zaciśnięcie"
3. Właściwości trzech funkcji pola
4. Końcowe wnioski

1. Wstęp - Bawiąc się liczbami
Bawiąc się liczbami człowiek siłą rzeczy zostaje matematykiem. A gdy już zostanie matematykiem, to czasem uda mu się trafić na niezwykle ciekawą matematyczną zależność. Od bystrości umysłu zależy, czy ta zależność zostanie zauważona. Chyba zdarzyło się autorowi mieć w odpowiednim czasie dostateczną bystrość umysłu, bo zauważył następującą zależność... chwileczkę... Zanim będzie przedstawiona ta zależność, można zapytać Czytelnika: czy jest taka możliwość, aby suma różnych liczb, czyli a+b, była równa iloczynowi tych samych liczb, czyli a*b? Oczywiście, dla czytelnika jest to proste pytanie, więc zna odpowiedź - trzeba rozwiązać równanie z dwoma niewiadomymi. Rozwiązań tego równania jest nieskończenie wiele. Aby o tym się przekonać, trzeba pod jedną z "niewiadomych" - a lub b - podstawić dowolną liczbę i (z powstałego w taki sposób równania z jedną niewiadomą) wyliczyć wartość drugiej niewiadomej liczby. W ten sposób można przekonać się, że mamy nieskończenie wiele par liczb, które są ze sobą związane - wiąże je ze sobą właśnie wymieniona zależność: a+b=a*b.

Można by zadać pytanie... Czy jest możliwe, aby wszystkie te liczby, będące rozwiązaniami przedstawionego równania (albo conajmniej pewna ich część), były ze sobą powiązane jeszcze za pomocą jakichś innych funkcji? A jeżeli tak, to jaka jest postać tych nieznanych funkcji? Wydaje się, że rozwiązanie tego zagadnienia przekracza ludzkie możliwości.
Autorowi udało się trafić na rozwiązanie dla podobnej, ale nieco bardziej złożonej zależności (równania) - ta zależność ma postać: (a+b)/2=(a*b)^0.5. Przedstawia ona symbolicznie równość między średnią arytmetyczną i średnią geometryczną z liczb a i b. Rozwiązaniem dla tego równania (ale tylko przybliżonym rozwiązaniem) są dwie eksponencjalne funkcje, które można by oznaczyć literami a i b.

Zanim nastąpi dalszy ciąg, jeszcze tylko mała zamiana... Zamieńmy tutaj oznaczenia i zamiast oznaczać liczbę (albo funkcję) jako "a" w dalszej części artykułu niech będzie ona oznaczona jako "Vel". W tym miejscu zapamiętajmy również to, że w ten sposób została symbolicznie oznaczona funkcja, którą będziemy nazywali "funkcją potencjału z eksponencjalnym rozluźnieniem" (indeks przy "V" jest skrótem od nazwy: "eksponencjalne rozluźnienie" - po angielsku "exponential looseness", czyli w skrócie "el"). (Do czego nawiązuje ta nazwa potencjału i indeks w symbolicznym oznaczeniu potencjału, to okaże się w dalszej części artykułu.) Zamieńmy też oznaczenie liczby z "b" na "Vet". Zapamiętajmy także, że w ten sposób została symbolicznie oznaczona funkcja, którą będziemy nazywali "funkcją potencjału z eksponencjalnym zaciśnięciem" (indeks przy "V" jest skrótem od nazwy "eksponencjalne zaciśnięcie" - po angielsku "exponential  tightness", czyli w skrócie "et".
Równanie, wyrażające symbolicznie równość między średnią arytmetyczną i średnią geometryczną, można więc zapisać w postaci: (Vel+Vet)/2=(Vel*Vet)^0.5.

2. Dlaczego "rozluźnienie" i "zaciśnięcie"
Aby nie trzymać dłużej Czytelnika w niepewności w sprawie nazw wymienionych funkcji, wyjaśnijmy, że będziemy tutaj zajmowali się funkcjami, które można zastosować do opisu grawitacyjnego potencjału zarówno ciał niebieskich, jak i pojedynczych cząstek materii. Należy nadmienić, że od dawna jest znane rozwiązanie dotyczące grawitacji, jakie podał Isaak Newton. Według grawitacyjnego prawa Newtona wzajemne oddziaływanie między dwoma materialnymi ciałami jest odwrotnie proporcjonalne do kwadratu odległości. To wzajemne oddziaływanie nawiązuje do pojęcia siły, ale tutaj będziemy skupiali się na wzajemnym przyśpieszeniu, jakie uzyskuje każde z ciał z powodu istnienia swojego sąsiada. Funkcja przyśpieszenia, która opisuje przyśpieszenie danego ciała, jest tożsama z funkcją natężenia grawitacyjnego pola jego sąsiada. To sąsiednie ciało charakteryzuje się właśnie tym, że opisują go takie parametry, jak natężenie pola E oraz potencjał pola V. Z tego względu, że opis tego pola pochodzi od Newtona, potencjał pola można tu zapisać z indeksem "n", czyli Vn=A*B/x, a natężenie pola można zapisać En=dV/dx=d(A*B/x)/dx=-A*B/x^2.

W tym miejscu należy wyjaśnić, że istniejący w przedstawionych wzorach iloczyn A*B jest współczynnikiem. Zastępuje on we wzorach inne współczynniki, które są stosowane we wzorach Newtona, czyli G (stałą grawitacyjną) oraz M (masę). Konkretny przykład takiej zamiany można obejrzeć w zapisanych poniżej funkcjach (przedstawionych razem z ich wykresami). Pierwszy z występujących tam wzorów to wzór na natężenie grawitacyjnego pola wg Newtona En, a następne w kolejności to Eel i Eet. Należy tu zwrócić uwagę na fakt, że iloczyn wartości M (masy Ziemi) i stałej grawitacyjnej G jest równy 3,975112754*10^14. Ale ten sam iloczyn jest równy iloczynowi współczynnika proporcjonalności A i współczynnika eksponencjalnego B, czyli A*B. (Jest to ważne dla funkcji Eel i Eet.) W tym przypadku wartość współczynnika eksponencjalnego B=1,76612818375*10^4 i wartość współczynnika A=(3,975112754*10^14)/(1,76612818375*10^4)=2,25074985529*10^10.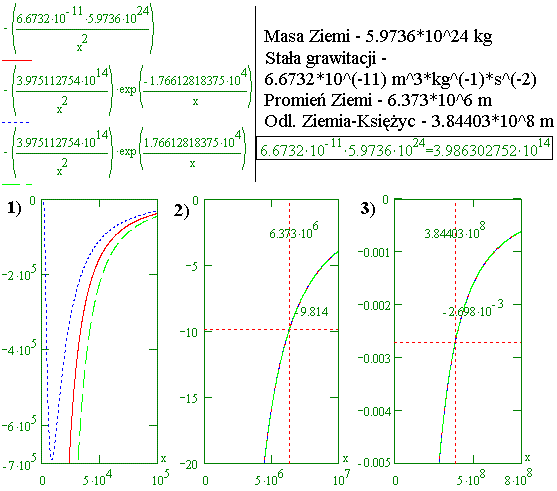

Z pewnego punktu widzenia, ta zamiana współczynników ma charakter formalny. Ale z innego punktu widzenia, ułatwia ona dostrzeganie istniejących zależności. Liczby we wzorach mają jedynie względny charakter i ich wartość (w powiązaniu z grawitacyjnymi właściwościami materii) zależy wyłącznie od umownie  przyjętych jednostek miar (masy, długości itd.). Dlatego skupiamy się tutaj jedynie na relacjach, jakie istnieją między liczbami i funkcjami. Aby to ułatwić, żadne miana jednostek miary przy liczbach nie występują. Liczby i funkcje, nie kojarząc się z umownymi jednostkami miary, mówią  same za siebie.

Co tyczy się pojęć "rozluźnienie" i "zaciśnięcie", to są one związane z orbitami, po jakich poruszają się ciała, gdy tworzą stabilny układ. Gdyby potencjał i natężenie pola grawitacyjnego ciał zmieniały się dokładnie według prawa Newtona, czyli gdyby miały postać: Vn=A*B/x i En=-A*B/x^2, to wówczas orbity ciał miałyby idealny kształt - byłyby elipsami bądź okręgami. Gdy w stabilnym wirującym układzie dwóch ciał parametry pola - potencjał i natężenie pola - odbiegają od tych, jakie są opisywane przez prawo Newtona, to wówczas zamiast elipsy powstaje albo orbita z rozluźnieniem pętli trajektorii, albo orbita z zaciśnięciem pętli trajektorii. Tego rodzaju orbity są przedstawione na poniższych rysunkach.

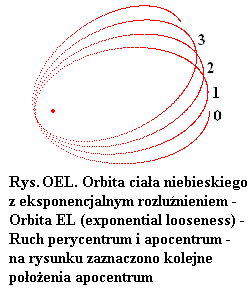
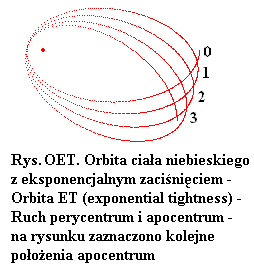
O eliptycznej orbicie można powiedzieć, że powstaje ona w postaci zamkniętej linii dzięki szczególnemu zbiegowi okoliczności. Ten zbieg okoliczności jest po prostu związany z tym, że funkcja grawitacyjnego pola, które (w pewnym sensie) kieruje przyśpieszeniem ciała na orbicie, ma akurat taki, a nie inny, przebieg. Dzięki akurat takiemu przebiegowi zmian grawitacyjnego pola ciało po jednym obiegu na orbicie trafia dokładnie na tę samą trajektorię, po której poruszało się podczas poprzedniego obiegu na orbicie. Rozluźniona orbita bądź zaciśnięta orbita powstaje wówczas, gdy rozkład grawitacyjnego pola jest taki, że uniemożliwia powtarzanie ruchu po eliptycznej orbicie.

Przyśpieszenie w takim grawitacyjnym polu (w stosunku do przyśpieszenia, jakie jest opisywane w prawie Newtona) jest albo zwiększone, albo zmniejszone. Zwiększone przyśpieszenie jest przyczyną tego, że ciało szybciej porusza się do miejsca, które jest maksymalnie oddalone od centrum pola (czyli od jednego maksymalnego oddalenia do następnego maksymalnego oddalenia). Wskutek tego dotrze ono tam wcześniej, zanim upłynie czas wykonania jednego pełnego obrotu ciała na orbicie. Zatem nie trafi ono w to samo (maksymalnie oddalone od centrum) miejsce na orbicie, w którym ono było podczas poprzedniego obrotu. Powstaje więc orbita z eksponencjalnym rozluźnieniem.
Natomiast zmniejszone przyśpieszenie w grawitacyjnym polu jest przyczyną tego, że ciało wolniej porusza się do miejsca, które jest maksymalnie oddalone od centrum pola. Wskutek tego dotrze ono tam dopiero wówczas, gdy już upłynie (i zostanie przekroczony) czas wykonania jednego pełnego obrotu ciała na orbicie. W ten sposób powstaje orbita z eksponencjalnym zaciśnięciem.

Dla ścisłości należy tu zwrócić uwagę na rzecz oczywistą, a mianowicie taką, że ruch obrotowy ciała na orbicie nie jest jednostajny. Ten ruch obrotowy również zmienia się pod wpływem zmian potencjału grawitacyjnego pola. Zatem ten rodzaj wyścigu, który decyduje o tym, jaki typ orbity powstanie (orbita wg Newtona, orbita z rozluźnieniem czy orbita z zaciśnięciem), występuje między zmieniającym się kątem obrotu wektora wodzącego ciała i zmieniającą się długością tego wektora. (Ma się rozumieć, że te relacje między kątem obrotu wektora i długością wektora są teoretycznymi relacjami, które istnieją w odpowiednim układzie współrzędnych.)

Wymienione orbity powstają w wyniku istnienia takiego przestrzennego rozkładu grawitacyjnego pola ciał, że jego potencjał grawitacyjny można opisać albo za pomocą funkcji potencjału z eksponencjalnym rozluźnieniem Vel i funkcji natężenia tego pola Eel, albo za pomocą funkcji potencjału z eksponencjalnym zaciśnięciem Vet i funkcji natężenia tego pola Eet. Te matematyczne funkcje oraz ich wykresy są przedstawione na poniższych rysunkach.

Właśnie w opisach przedstawionych funkcji została zastosowana dowolność w wyborze wartości liczb dla określenia parametrów. Występują one bez jednostek miar. Bo te funkcje nie opisują grawitacyjnego pola żadnego konkretnego ciała bądź cząstki i nie odwołują się do żadnego układu miar.
 

3. Właściwości trzech funkcji pola
Jedna z interesujących zależności między funkcjami natężenia pola Eel, En i Eet jest taka, że przy każdej (dowolnej, ale dodatniej) odległości x bezwzględna wartość natężenia pola En jest równa średniej geometrycznej wyliczonej z bezwzględnych wartości natężenia pola Eel i natężenia pola Eet, czyli En=A*B/x^2=(Eel*Eet)^0.5=((A*B/x^2)*exp(-B/x)*(A*B/x^2)*exp(B/x))^0.5=A*B/x^2.

Na wykresach widać, że przy dużych odległościach x od centrum każdego z tych trzech pól ich parametry zmieniają się w podobny sposób. Zatem również i średnia arytmetyczna z wartości parametrów (przy konkretnej odległości x) jest bardzo zbliżona do średniej geometrycznej z tych wartości parametrów. Czyli można napisać, że .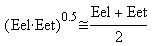
Przy rosnących wartościach odległości x od centrum każdego z tych pól różnica między tymi polami staje się coraz mniejsza, czyli również coraz mniejsza jest różnica między średnią geometryczną i średnią arytmetyczną wartości tych funkcji pola. Taki wniosek można wyciągnąć na podstawie przedstawionych powyżej oraz na podstawie poniższych wykresów.

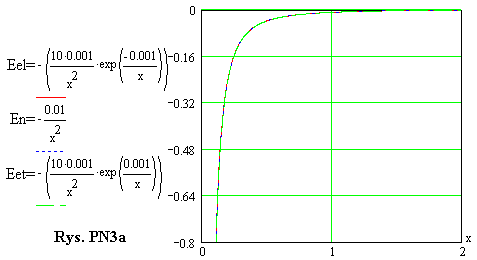
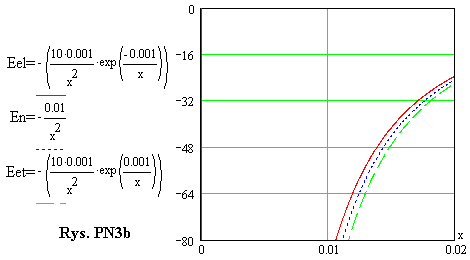
Przedstawione na tych rysunkach wykresy są identyczne jak na rys. PN2a i PN2b, a zostały one tu powtórzone także dlatego, aby Czytelnik (bez konieczności obliczania pochodnych funkcji) mógł porównać strukturę funkcji Eel i funkcji Eet ze strukturą funkcji En oraz porównać ze sobą przebiegi tych funkcji w układzie współrzędnych.
A wracając do porównywania ze sobą średniej arytmetycznej i średniej geometrycznej, czyli do przybliżonego równania 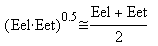, zmniejszanie się różnicy między tymi średnimi, które następuje przy wzroście odległości x od centrum pola, można także obejrzeć na dwóch poniższych przykładach obliczeniowych.

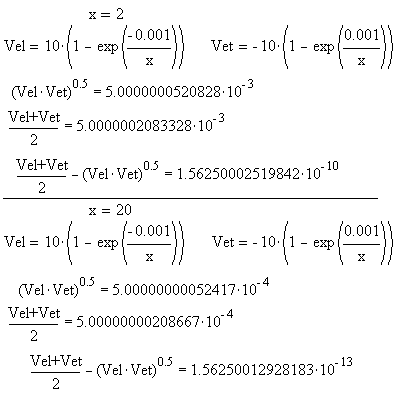
Co prawda, przykłady te dotyczą średniej arytmetycznej i średniej geometrycznej z dwóch funkcji potencjału pola, a nie funkcji natężenia pola, ale relacje między przebiegami tych funkcji (co widać na wykresach - rys. PN1b i rys. PN2b) są do siebie podobne. Zatem, jak widać, dla równania (a+b)/2=(a*b)^0.5 mamy tutaj dwie postaci rozwiązań, dwa komplety funkcji, przy czym te komplety rozwiązań - matematyczne funkcje - są ze sobą matematycznie spowinowacone w ten sposób, że jedne są wyjściowymi funkcjami, a drugie - to są pochodne od tych funkcji.

4. Końcowe wnioski
Na podstawie powyższego można wyciągnąć najważniejszy wniosek, który dotyczy stałej grawitacyjnej G - ten współczynnik dla różnych ciał niebieskich, a także i dla różnych cząstek, nie jest wcale wartością stałą. (Nie idzie tu bynajmniej o to, że będzie on różny przy stosowaniu różnych układów miar.) Z czego wynika to, że wartość G jest różna dla różnych ciał i cząstek? Przede wszystkim ten wniosek wynika właśnie z tego, że grawitacyjne prawo Newtona, czyli wzór En=G*M/x^2, nie opisuje dokładnie grawitacyjnych pól istniejących w przyrodzie ciał niebieskich. O tej niedokładności wzoru Newtona świadczy istnienie ruchu peryhelium planet w Układzie Słonecznym oraz ruchu perycentrum gwiazd podwójnych, na przykład, jak w przypadku gwiazdy podwójnej PSR B1913+16. A takich ruchów grawitacyjne prawo Newtona nie przewiduje - zgodnie z nim (a ściślej rzecz biorąc, na podstawie wynikającego z tego prawa wniosku), gdy nie ma zewnętrznych zakłóceń, dwa orbitujące ciała, np. w postaci gwiazdy podwójnej, powinny poruszać się po eliptycznych orbitach.

W artykule są przedstawione dwie matematyczne funkcje natężenia pola, które pod względem strukturalnym (zwłaszcza przy dużych odległościach) są zbliżone do funkcji natężenia pola wg Newtona, a prowadzone za ich pomocą obliczenia dają niemal identyczne wyniki. Oczywiście, tak dzieje się przy odpowiednim doborze współczynników A i B dla funkcji Eel i Eet. Jedna z tych funkcji, a konkretnie, funkcja natężenia pola z eksponencjalnym zaciśnięciem Eet, ma taką budowę strukturalną, że zmieniając wartości współczynników A i B można za jej pomocą opisywać ruchy orbitalne różnych ciał niebieskich, w których występują różne stopnie zaciśnięcia orbity. Dobrane współczynniki A i B, służące dla określania grawitacyjnego pola danego ciała, będą charakterystycznymi parametrami akurat dla danego ciała. W przypadku innego ciała niebieskiego, w polu którego orbita poruszającego się ciała będzie miała zupełnie inny stopień zaciśnięcia, będą to już zupełnie inne wartości współczynników A i B.

Jeśli zastosować przeliczenie odwrotne, czyli zamiast iloczynu A*B (gdy znana jest jego wartość) wykorzystać iloczyn G*M i z wartości tego iloczynu wyliczyć znanym dotychczas sposobem masę M, to przyjmując G jako stałą wartość otrzymuje się w rezultacie fałszywy wynik dotyczący wartości masy M.
Można przypuszczać, że parametr G dla ciał niebieskich z Układu Słonecznego jest w przybliżeniu stały. Decydujący wpływ na wartość tego parametru ma Słońce. Dla planet US różnice między wartościami parametru G są tak małe, że są niezauważalne. Duża różnica między masą każdej planety US i masą Słońca sprawia, że w oddziaływaniach dominuje Słońce. Jest to sytuacja podobna do tej, z jaką miał do czynienia Galileusz, gdy zrzucał kamienie o różnej masie z wysokiej wieży. Wówczas w jego doświadczeniach decydującą rolę odgrywała Ziemia i nie widać było, aby kamienie o różnej masie spadały z wieży w odmienny sposób. Zatem dla warunków, jakie istnieją w Układzie Słonecznym wartość parametru G można uważać za stałą, bo różnice są tak małe, że niemal niewykrywalne. Ale stosowanie tej samej wartości G w obliczeniach dla całego kosmosu, a szczególnie dla niezwykle masywnych ciał niebieskich, które są składnikami gwiazd podwójnych, będzie niewątpliwie prowadzić do błędnego oszacowania masy tych ciał.

Na tę sprawę należy spojrzeć jeszcze szerzej... Wartość parametru G dla Układu Słonecznego jest zupełnie inna, aniżeli wartość G, jaka jest wyliczana na podstawie wyników grawitacyjnego oddziaływania ze sobą dwóch mas rzędu kilku czy kilkunastu kilogramów w doświadczeniu laboratoryjnym. Czyli zastosowanie wartości G, która jest określana na podstawie laboratoryjnych doświadczeń, do obliczania parametrów ciał niebieskich z Układu Słonecznego również prowadzi do błędnego obliczenia mas tych ciał niebieskich.

Wymienione błędy obliczeniowe dotyczące masy ciał niebieskich, jakie powstają za przyczyną przyjęcia błędnego założenia, że G jest stałą wartością, są wystarczająco ważnym powodem, aby zrewidować dotychczasowe poglądy i po nowemu spojrzeć na grawitacyjne oddziaływania ciał niebieskich i ich cząstek składowych.

Przedstawione funkcje Eel i Eet mogą być używane dla opisu pola zarówno dla ciał niebieskich, jak i dla pojedynczych cząstek materii. Dotychczas nie stwierdzono, aby w przyrodzie istniały grawitacyjne pola, w których występowałyby rozluźnione orbity ruchu ciał bądź cząstek. Ale takie orbity mogą zostać odkryte w przyszłości.  A gdyby nawet w przyrodzie podobnego typu orbit nie było, to funkcja natężenia pola z rozluźnieniem Eel doskonale nadaje się do wyjaśniania i interpretacji przyrodniczych zjawisk, które istnieją w nanoskali.
______________________________________

Bogdan Szenkaryk "Pinopa"
Polska, Legnica, 2013.05.26.