Błąd w matematyce

Podtytuł: Mój błąd... Rewolucji w nauce nie będzie

Przyznaję, że w tym artykule pobłądziłem... Kto chce, może zapoznać się z tym błędem, czytając artykuł i komentarze pod nim. Wyjaśnienie, na czym polegał błąd, znajduje się w komentarzu Pinopy z dnia 11.06.2014 09:33.

*     *     *

Na stronie internetowej http://www.matemaks.pl/liczby-i-dzialania.php?tid=139  można przeczytać:
"Liczbę Eulera (zwaną również pod nazwą liczby Nepera) oznaczamy krótko literą e. Wartość tej liczby można określić w przybliżeniu:

Liczbę e można definiować na wiele różnych sposobów. Najczęściej spotykana jest definicja wykorzystująca następującą granicę:

 

Równie często definiuje się liczbę e jako sumę szeregu:

 

Powyższy wzór można z powodzeniem wykorzystywać do obliczania wartości liczby e z dużą dokładnością. Suma zaledwie 10 pierwszych wyrazów tego szeregu, daje całkiem niezłe oszacowanie liczby Eulera."

W matematyce są jeszcze inne sposoby obliczania liczby e, ale tutaj będzie mowa o błędzie, który wiąże się z pierwszą z podanych tu definicji liczby e. Bo granicą, o której jest mowa w tej definicji, nie jest liczba e, lecz liczba 1. Zatem poprawny zapis tej granicy powinien mieć postać:

Przy tym należy tu dodać o istnieniu "perturbacji" wartości funkcji (1+1/n)^n, gdy wartość liczby n staje się coraz większa. Ale po kolei...

Gdy spojrzeć na wykres funkcji (1+1/n)^n, który jest przedstawiony na Rys. e_a, A),

to widać, że wartość funkcji dąży do wartości e. I to dążenie widać jeszcze w pobliżu wartości n=6,16*10^4 - bo akurat przy tej wartości n wartość funkcji wynosi  2,71825976480371. Ale perturbacje wartości funkcji zaczynają się, zanim jeszcze wartość n będzie równa 10^14,7.  Na Rys. e_a, B) widać, że podczas tych perturbacji wartości funkcji zmieniają się w postaci pewnych skoków. Wartości funkcji stają się albo coraz większe od e, albo coraz mniejsze od e. W końcu funkcja ta rośnie do maksymalnej wartości 7,38,  czyli ponad dwukrotnie przekracza wartość liczby e, ażeby następnie skokowo zmniejszyć się do wartości 1. Wzrost wartości funkcji na krótko przed skokiem oraz skok wartości funkcji, która, zgodnie z oczekiwaniem, ma dążyć do e, jest pokazany na Rys. e_b oraz na Rys. e_c.

Ktoś może tu powiedzieć, że to są jakieś błędy komputera. Wychodzą one na jaw w takiej, a nie innej postaci, z powodu ograniczonych zdolności obliczeniowych komputerowego programu i zaokrągleń wyników obliczeń.
Bo przecież  można udowodnić, że... i tu można by podać dowód tego, że  przy n rosnącym do nieskończoności ciąg , w którym , jest niemalejący i ograniczony z góry, a zatem jest zbieżny. Ale jest tu poważne zastrzeżenie - ten dowód wcale nie dowodzi zbieżności wyrazów ciągu do wartości liczby e.

W tej sytuacji można by powiedzieć, że ona "brzydko pachnie".  Bo najczęściej jako wartość liczby e podaje się zależność , ale do obliczania wartości liczby e jest używana zależność z innej definicji (tak dzieje się najczęściej), a mianowicie, oblicza się, na przykład, według zależności .

I bardzo dobrze, że do obliczania liczby e używana jest zależność wg drugiej definicji, a nie pierwszej.  Bo, jak widać na Rys. e_d i Rys. e_e, istnieje pewna średnia wartość wyrazów ciągu, która (jak można przypuszczać) zbliża się do wartości liczby e.

Ale kolejne wartości coraz bardziej odbiegają od wartości liczby e. Czyli, praktycznie rzecz biorąc, na postawie funkcji nie można obliczyć liczby e z dokładnością do 50-tego miejsca po przecinku, tak jak podano w cytacie (na początku artykułu).
Należy tu podkreślić, że na wykresach wartości n zmieniają się w sposób ciągły, a nie jako ciąg kolejnych liczb naturalnych N. Ale dla sensu przedstawionego tutaj wywodu ten fakt nie ma znaczenia. Poniżej przedstawione są dwa przykłady obliczeniowe wyrazów ciągu dla kolejnych dwóch liczb całkowitych.

W przykładzie A) dla kolejnych dwóch liczb n: n=5*10^8 i n=5*10^8+1, różnica między wartościami wyrażeń ciągu występuje na 8-mym miejscu po przecinku, natomiast różnica między wartościami tych wyrażeń i liczbą e występuje już na 7-mym miejscu po przecinku. W przykładzie B) dla dwóch kolejnych liczb, ale o 6 rzędów większych niż w przykładzie A), różnica między wartościami kolejnych wyrażeń ciągu występuje dopiero na 14-tym miejscu po przecinku, ale różnica między wartościami tych wyrażeń i liczbą e występuje już na 3-cim miejscu po przecinku.

Możliwe jest, że powyższe cyfrowe wywody są błędne z powodu błedów, jakie były popełniane przez maszynę cyfrową. Poniżej są przedstawione przykłady obliczeń, które można sprawdzić na innym, być może, dokładniejszym komputerze

A poniżej jest przedstawiony dowód, w postaci prostych matematycznych przekształceń, wykazujący prawdziwość przedstawianych tu matematycznych faktów.

Równanie początkowe jest równaniem z jedną niewiadomą. Mając to równanie, zadajemy sobie pytanie: jaką wartość musi mieć niewiadoma n, aby to równanie było prawdziwe? Po kilku krokach dochodzimy do wniosku, że to równanie jest prawdziwe wówczas, gdy n dąży do nieskończoności.
Ten dowód w postaci przekształceń można przedstawić w odwrotnej kolejności.

 

Można tu wyróżnić cztery kroki - cztery kolejne przekształcenia:
1. "jeśli n dąży do nieskończoności, to 1/n=0"; jest to wyjściowe równanie,
2. "dodanie do obu stron równania liczby 1 nie zmienia poprawności tego równania",
3. "pierwiastek n-tego stopnia i potęga n-tego stopnia nie zmienia lewej strony równania" oraz "podniesienie liczby 1 z prawej strony równania do dowolnej potęgi nie zmienia liczby 1",
4. "podniesienie obu stron równania do potęgi n-tej nie zmienia równania, ale usuwa operację pierwiastkowania obu stron równania".
W wyniku tych przekształceń otrzymuje się zależność (1+1/n)^n=1.

Na koniec warto wspomnieć o konsekwencjach tego faktu, że w matematyce i innych naukach ścisłych, w przeprowadzanych tam obliczeniach, w wielu logicznych wywodach i matematycznych dowodach, zamiast poprawnej zależności, była wykorzystywana błędna zależność . Konsekwencje tego faktu są takie, że wszystkie te obliczenia, logiczne wywody i matematyczne dowody były błędne. Z tych błędnych wyników korzysta się powszechnie w nauce i technice, a szkody, jakie zostały wskutek tego poczynione, są zapewne wielkie, ale trudne do oszacowania. Ale, niewątpliwie, niezbedne jest naprawienie tych szkód.

Ta błędna zależność była wykorzystywana, bo umożliwiała ona wykonywać w obliczeniach wiele uproszczeń i pozwalała uzyskiwać "niezwykłe" wyniki.  Takie obliczeniowe efekty byłyby niemożliwe do uzyskania, gdyby korzystano z poprawnej zależności . Bo, po prostu, ta zależność w tych wszystkich obliczeniach, wywodach i dowodach nigdy nie byłaby wykorzystywana i nie doszłoby do popełnienia tak wielu błędów. Bo do takich obliczeń, wywodów i dowodów, jakie były przeprowadzone przy wykorzystaniu błędnej zależności , poprawna zależność  się nie nadaje. ...Nie nadaje się ona do popełnienia tak rażących (pomimo że dotychczas istniejących w ukryciu) błędów, bo żadnych "niezwykłych" wyników z liczbą 1, podnoszoną do różnych poteg, uzyskać nie można. Bo w wyniku zawsze wyjdzie liczba 1.

Dzisiaj przed światem nauki stoi dość trudne i kosztowne zadanie - z nauki i praktyki należy wyrugować ten błędny wzór. Nie będzie to łatwe... Ale poprawienie tego błędu doprowadzi do postępu zarówno w naukach ścisłych, jak i w tych wszystkich dziedzinach ludzkiej działalności, gdzie są stosowane osiągnięcia nauk ścisłych. *)
_____________________________________
*) Jak dużo pracy będzie miało wiele osób, można zorientować się na drobnym przykładzie internetowej strony, z ktorej pochodzi urywek tekstu, cytowany na początku tego artykułu. W związku z podstroną http://www.matemaks.pl/granica-ciagu.php?tid=10104  autor będzie miał bardzo wiele roboty - oczywiście, jeśli zechce z tej podstrony oraz z innych wskazanych tam podstron (za pomocą odnośników) usunąć błędy. Bo podstrona nosi tytuł: "Granice ciągów z liczbą e".
To był tylko drobny przykład... Bo ogrom pracy jest związany z przeprowadzeniem w różnych dziedzinach zupełnie nowych obliczeń, wywodów i matematycznych dowodow, z napisaniem nowych podręczników, które nie zawierałyby już opisanej tu błędnej zależnosci, oraz z wprowadzeniem tych podręczników do szkolnictwa średniego i wyższego.
Pocieszeniem może być to, że w tej wielkiej pracy muszą brać udział ludzie z różnych krajów, bo ten błąd jest "błędem światowym", zadomowionym we wszystkich krajach, i wszystkie kraje będą musiały go wyrugować u siebie. Ale przy tym mogą sobie wzajemnie pomagać.
______________________________________

Bogdan Szenkaryk "Pinopa"
Polska, Legnica, 2014.06.09.

(Z błędną treścią powyższej notki - ale z rysunkami i wzorami - można zapoznać się na
http://pinopa.narod.ru/Blad_w_matematyce.pdf)

Uzupełniono dopisując poniższy komentarz Pinopy dnia 27.05.2018 r.

Pinopa

Przyznaję... mój błąd! Rewolucji w matematyce nie będzie!Przyznaję... mój błąd!
Nikt nie potrafił wskazać błędu w kilku wnioskach, które przedstawiałem i które były związane z kolejnymi przekształceniami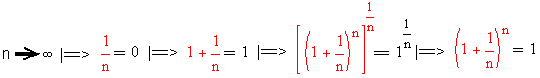

i ja tam także nie znajdowałem błędu. A błąd jest związany z tym, że w wyrażeniu (1+1/n)^n składnik 1/n zmniejsza się do 0 wolniej (przy wzroście wartości n), aniżeli następuje wzrost "końcowej" wartości wskutek podnoszenia do potęgi n.

Błąd odkryłem korzystając z przekształcenia a^b=e^(b*ln(a)). Opierając się na tej podstawie można zapisać: (1+1/n)^n=e^(n*ln(1+1/n)). Patrząc na prawą stronę tej równości można sobie zadać pytanie, które dotyczy prędkości wzrostu i prędkości zmniejszania się dwóch czynników iloczynu, który znajduje się w wykładniku potęgi. Jeden z tych czynników (a konkretnie, n) rośnie do nieskończoności, a drugi czynnik (czyli ln((1+1/n)) maleje do zera. Pojawia się więc tu pytanie, czy te prędkości wzrostu i zmniejszania się czynników zrównoważą się i wykładnik potęgi będzie dążył do 1- wtedy będzie (1+1/n)^n=e, czy też przeważy prędkość dążenia jednego z czynników do zera - wtedy będzie (1+1/n)^n=1.
W najprostszy sposób, bo korzystając z metody cyfrowej i komputera, można na wykresie zobaczyć, że wzrost i zmniejszanie się czynników w wykładniku potęgi równoważą się nawzajem.

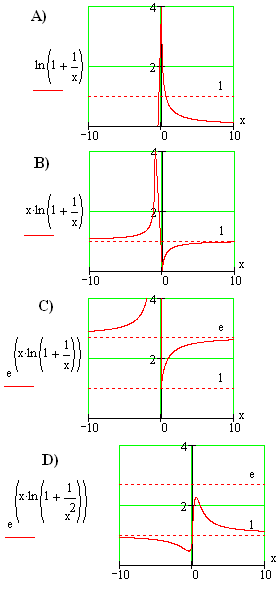
Ten fakt jest widoczny na wykresie B) - widać tam, że iloczyn w wykładniku jest równy 1. Zatem prawdą jest, że (1+1/n)^n=e.
Posiłkuję się tutaj prędkościami wzrostu i zmniejszania się czynników w wykładniku potęgi e^(n*ln(1+1/n), aby (korzystając z okazji) wskazać, że to właśnie te prędkości decydują o wyniku, czyli decydują o tym, czy w wykładniku potęgi e^(n*ln(1+1/n)) znajdzie się liczba 1 czy 0.
Tę zależność widać na wykresie D). Tam specjalnie zmieniłem prędkość zmniejszania się jednego z czynników do zera (podnosząc w mianowniku x do potęgi 2, drugi czynnik pozostawiając bez zmiany), aby pokazać, że wzrost i zmniejszanie się czynników w wykładniku potęgi mogą nie równoważyć się i w efekcie wykładnik (przy wzroście n) może dążyć do 0.
Moje błędne wnioskowanie można więc w pewnym sensie wyjaśnić tym, że (zapewne w podświadomości) nieprawidłowo oceniłem szybkość zmniejszania się ułamka 1/n - przypisywałem mu większą szybkość zmniejszania się przy wzroście wartości n, aniżeli ta szybkość zmniejszania się, jaka jest w rzeczywistości.
11.06.2014 09:33