(O welocetyzerze, który nie jest zabawką)
Nie jest? To dlaczego sprawia tyle radości?
„Księga mądrości króla Juliana”
Niniejsza notka jest nieprzyzwoicie długa i operuje niezwykle poważnymi pojęciami. Nie chciałbym jednak, żeby była odbierana zbyt poważnie. W końcu to żart, mający „przetestować” elementy znane z uczonych tomiszczy, opisujących fizykę teoretyczną. A ponieważ każdy lubi żarty, zapraszam do lektury.
Budujemy zbiór „trójmianowy”
Na początek zastanówmy się, jak opisać wszystkie wielomiany stopnia drugiego. Te, które tworzą najznańsze równania kwadratowe, co przy ich rozwiązywaniu zerowych liczy się deltę. Są to funkcje postaci:
fabc(x) = ax2 + bx + c
Każdy trójmian określony jest przez trzy liczby: a, b, c. A to przecież punkt z R3. Czyli przestrzeń trójmianów, której można sobie nie wyobrażać (czy ktoś może sobie wyobrazić zbiór funkcji?), jest opisywana przez prawie zwyczajną przestrzeń trójwymiarową.
Napisałem „prawie”, bo musimy zastanowić się nad punktami dla których a=0. No bo jeśli a=0, to nasze równanie nie jest równaniem kwadratowym. Na pierwszy rzut oka nie wydaje się to jakoś strasznie istotne, ale jak przypomnimy sobie przepis na wyliczanie pierwiastków, to okaże się, że wymaga on dzielenia przez a. A mając w pamięci prastarą prawdę, zapisaną w wielkiej księdze matematyki: „nie dziel cholero przez zero”, uznajmy, że punkty postaci (0, b, c) nie będą należały do naszego zbioru.
W sumie to kwestia wyboru, jakie zagadnienia związane z funkcjami kwadratowymi będziemy chcieli badać. Jeśli interesują nas własności liniowe (dodawanie funkcji i mnożenie je przez liczby), wtedy dopuszczamy do zbioru trójmianów funkcje liniowe, jako szczególne przypadki funkcji kwadratowych w których a=0. Przy takim wyborze badany zbiór jest zwykłą przestrzenią wektorową i nie usuwamy z niej płaszczyzny a=0. Gdy jednak zajmujemy się procedurą znajdowania pierwiastków i pokrewnymi jej problemami, trzeba będzie wprowadzić ograniczenie na nasz zbiór: a≠0.
Tak więc nasz zbiór będzie trójwymiarową przestrzenią z usuniętą płaszczyzną. Oznaczę sobie ją symbolem V i z braku lepszej nazwy nazwę przestrzenią trójmianową.
V = R3\R2
W poprzednim odcinku podałem przykład, w którym przyrodzone bogactwo Rn zostało ograniczone do możliwości odczytywania współrzędnych. Pora więc przedyskutować, jakie typowe cechy R3 warto będzie zostawić przy pracy nad V.
- Dodawanie trójmianów jest równoważne dodawaniu punktów R3⊃V. Można więc pomyśleć, że traktowanie punktów V jak wektorów, ma uzasadnienie. Tyle, że dodawanie nie jest określone w całej przestrzeni, bo „nie da się” dodać punktów (a, … ) i (-a, … ). Czyli jednak w V nie mamy dodawania. Może to wyglądać na mały kłopot, ale w dalszej części tekstu nie będę dodawał czy odejmował od siebie trójmianów, więc mi to nie przeszkadza.
- „Długość” wielomianu – pierwiastek z a2+b2+c2 – nie ma sensu, za to w R3 jest kanoniczna. Dodawanie kwadratów a, b i c jest szczególnie rażące dla jakichkolwiek praktycznych zastosowań równań kwadratowych, bo liczby te mają inne jednostki. Chyba natknęliśmy się na przypadek, gdzie twierdzenie Pitagorasa „nie obowiązuje”.
- Skoro tak, to nie obliczymy „odległości” między punktami V. Tym bardziej, że i tak ma się ona nijak do tego, jak można liczyć odległości między funkcjami. Sensownej odległości nie ma, ale topologia/ciągłość narzucona przez √(a2+b2+c2) wydaje się być jak najbardziej OK. Przy czym nie oznacza to bynajmniej, że powyższy pierwiastek jest jakoś wyróżniony – równoważną ciągłość w V dostaniemy na wiele, zupełnie innych sposobów.
- Zbiór R3 daje nam kanoniczną definicję iloczynu skalarnego, a co za tym idzie pojęcie prostopadłości. Tutaj jest ona na nic, bo punkty to nie wektory. Zresztą można by się zastanawiać, czy w ogóle można rozsądnie zdefiniować w tej przestrzeni ortogonalność. Nie wiem, ale w trakcie prowadzonych (powierzchownych) badań nie znalazłem przesłanki mogącej sugerować pozytywną odpowiedź.
Jak widać mało jest rzeczy, które na dzień dobry przenoszą się z typowej Rn na nasz przypadek trójmianowej przestrzeni V.
Powstaje jednak pytanie, w co wyposażyć naszą V, żeby można się nią z pożytkiem pobawić? To, co najciekawsze , to wszelkie zagadnienia związane z wyliczaniem pierwiastków. Bo pamiętamy z lekcji matematyki w szkole średniej: na podstawie a, b, c znajdujemy deltę i dwa pierwiastki (w ogólności zespolone). Te i pokrewne tematy będą nam wskazywać drogę dla dalszych prac nad V.
Zanim przystąpimy do roztrząsania obiecanych bardzo poważnych zagadnień, małe podsumowanie czym dysponujemy. Mamy mianowicie:
- funkcje kwadratowe, których dziedziną jest prosta R. Nazwę sobie tę dziedzinę M, wtedy każdy trójmian wygląda następująco:
fabc: M ∋ x ↦ ax2 + bx + c ∈ R
- przestrzeń trójmianową V, której każdy punkt odpowiada jakiejś funkcji kwadratowej. Ponieważ zażądałem by pierwsza współrzędna a≠0, V będzie R3\R2 czyli innymi słowy będzie się składać z dwóch osobnych półprzestrzeni.
Celem niniejszej żartobliwej rozprawy, będzie przetestowanie kilku pojęć, używanych zwykle w fizyce matematycznej, na podstawie związków między zbiorami M i V.
Układy współrzędnych na V
Na razie na naszej V mamy jeden układ współrzędnych { a, b, c }. Pytanie czy przydadzą nam się jakieś inne układy współrzędnych?
Znane z innych zastosowań układy sferyczny i cylindryczny możemy od razu wyrzucić do kosza. Policzony „promień” r=√(a2+b2+c2) nie ma sensu, bo a, b i c mają inne jednostki – c możemy porównywać z a dopiero po pomnożeniu przez x2. Podobnie będzie miała większość krzywoliniowych układów. To znaczy: jak ktoś koniecznie chce je stosować, może to robić, nawet jeśli nie jest to zbyt mądre. W końcu 2+2 też może oznaczać dodawanie dwóch kilometrów drogi do dwóch kilogramów jabłek.
Są jednak pewne wyróżnione układy. Jakie? Żeby to dobrze zrozumieć, zwróćmy swoją uwagę na zbiór M, czyli dziedzinę wielomianów. M jest po prostu osią liczbową. Na owej prostej też możemy zmieniać układ współrzędnych. Zwykle nazywa się to zamianą zmiennych – jeśli tobie bardziej pasuje to określenie, to możesz sobie go właśnie używać. Wprowadźmy więc jakiś nowy układ/zmienną { y }. Jeśli związek między { x } i { y } będzie liniowy:
x = Ry + S gdzie R≠0
to funkcja od y też będzie trójmianem.
W(x) = ax2 + bx + c = a( Ry + S )2 + b( Ry + S ) + c = ...
= ( aR2 )y2 + ( 2aRS + bR )y + ( c + aS2 +Sb ) .
Mówi się, że zmiana układu współrzędnych nie zmienia postaci równania[1]. To, że inne transformacje na prostej produkują równania inne od kwadratowych zostawię jako ZTS.
Zobaczmy więc jak zmiana układu { x } na { y } przenosi się na przestrzeń trójmianową:
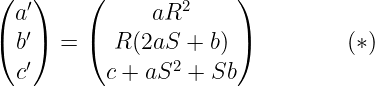
Każda para liczb R i S „produkuje” nowy układ współrzędnych w V. A każdemu takiemu układowi odpowiada jeden układ na M zależny w sposób liniowy od x. Zauważmy, że dorobiliśmy się „naturalnych” – może lepiej powiedzieć – wyróżnionych układów współrzędnych na przestrzeni V.
Niezmiennik
Zastanówmy się, czy przy okazji zamiany układu coś się nie zmienia? Na pewno liczba pierwiastków rzeczywistych, bo na przykład jeśli nasza funkcja kwadratowa nie miała miejsc zerowych, to po zmianie zmiennej na M również nie będzie ich miała. Nawiasem mówiąc, to cecha obowiązująca dla wszystkich zmian układu współrzędnych (nie tylko liniowych), więc gdybyśmy się ograniczyli do M, to nie byłoby się czym podniecać.
Skoro po zamianie zmiennej liczba pierwiastków się nie zmienia, to znaczy że znak nowej delty wyliczonej dla nowych współrzędnych, będzie zachowany. Jesteśmy o krok od znalezienia właściwego niezmiennika. Takiego który będzie już w sobie zawierał „znak delty”.
No bo czy jest coś, co jest takie samo niezależnie od wybranej zmiennej na M? Tak, są to wartości funkcji. Gdy przypomnimy sobie jak wyglądają wykresy funkcji kwadratowych (parabole), to okaże się, że zbiór wartości funkcji kwadratowej może być postaci: [q, ∞) dla a>0 lub (-∞ , q] dla a<0. Wartość q to współrzędna wierzchołka paraboli:
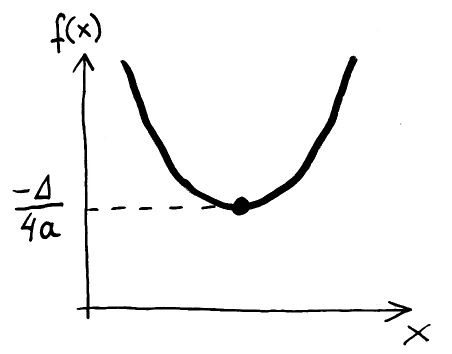
Wartość funkcji kwadratowej dla wierzchołka, podpowie nam postać funkcji na V, która będzie kandydatem na niezmiennik: q=-(b2-4ac)/(4a). I rzeczywiście – funkcja ta będzie miała dość ciekawą własność: Przekształcenia „naturalne” – te opisane wyżej jako (*) – będą zachowywać jej postać. Przyjrzyjmy się temu dokładniej.
Spostrzegawczy zauważą, że to cienkie. Bo co to znaczy „zachować postać funkcji”? Mamy zbiór, mamy funkcję. Wybór układu współrzędnych nie wpływa na wartość funkcji. Dla dowolnej zmiany układu, a nie tylko dla takiej jak powyżej. Pouczającym jest jednak, by przeliczyć jak będzie wyglądać funkcja q w innych współrzędnych. Ponieważ (*) pokazuje przejście { a',b',c' } → { a,b,c }, wystartujmy od funkcji q = -(b'2-4a'c')/(4a'), podstawmy (*), policzmy i poskracajmy co się da – oczywiście metodą ZTS. W wyniku otrzymamy, że q = -(b2-4ac)/(4a). Widzimy, że zmiana układu nie zmieniła postaci tej funkcji. Ale spróbujcie porządnie zdefiniować coś takiego jak „postać funkcji” ☺.
Zobaczmy jeszcze wykres zerowej poziomicy funkcji q – zauważmy, że z pominięciem osi C jest ona tożsama z zerową poziomicą Δ (rzecz jasna dla innych wartości poziomice q i Δ już się nie pokrywają). Dzieli ona każdą z połówek przestrzeni V na dwie części (a właściwie trzy, bo poziomica zerowa, to też osobny zbiór), które „mieszczą w sobie” wypisany wcześniej znak delty. Poziomica jest powierzchnią rozciągniętego w pionie stożka, rozpiętego na osiach C i A.
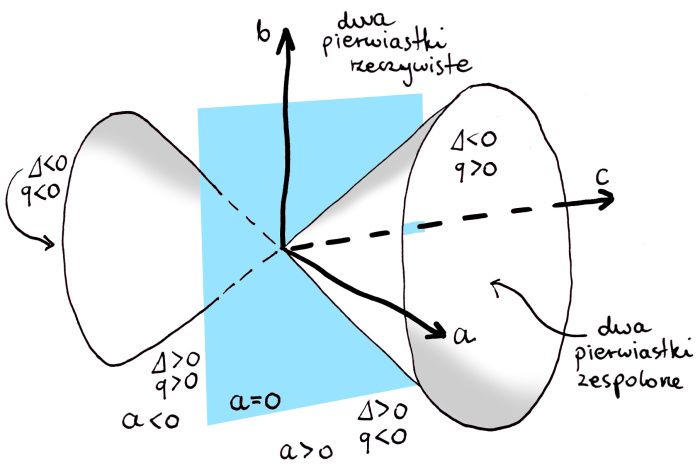
Błękitna płaszczyzna oznacza a=0. Punkty „wewnątrz” stożków
odpowiadają trójmianom bez rozwiązań rzeczywistych.
Jesteśmy już blisko rozwiązania, choć wielu na tym etapie się zatrzymuje: ma zbiór transformacji zachowujących postać równań; ma niezmiennik, czyli funkcję (w ogólności jakiś obiekt zbudowany z funkcji), której postać przy zmianie układu też jest zachowana. Ale to wszystko nieporządnicko niedodefiniowane. Pora więc dokonanie kolejnego kroku.
Symetrie
No dobra, podtytuł w końcu zapowiada, do czego dążyłem przez całą notkę. Zanim przejdę do owych symetrii, pora na powalające spostrzeżenie. Do tej pory zmienialiśmy układ współrzędnych na M, a co za tym idzie na V. Wybór układu współrzędnych jest kwestią techniczną i tak po prawdzie, nie powinno mieć to istotnego znaczenia. Oczywiście zgrupowanie układów współrzędnych postaci (*) nie jest głupie. Są one ważne, bo umiemy interpretować współrzędne w takich układach: są to po prostu współczynniki równań kwadratowych. Takiego luksusu nie mamy w przypadku innych układów dla przestrzeni V. Niemniej ciężko operować nieścisłym powiedzeniem „zachowuje postać funkcji”. Musimy znaleźć inny obiekt matematyczny, podobny z wyglądu do (*), żeby móc mówić całkiem poprawnie o symetriach. Takim obiektem są przekształcenia zbiorów M i V.
Czyli startujemy od odwzorowania (liniowego):
ψ: M → M
które w sposób opisany powyżej w (*) przenosi się na V:
φ: V → V
Wtedy niezmiennik ma mocny sens: to taka funkcja I na V, która nie zmienia wartości po przekształceniu dziedziny. Innymi słowy przekształcenie nie wychodzi poza poziomice funkcji I. Czyli dla każdego punktu p należącego do V mamy:
I(p) = I( φ(p) )
I to jest lepsza definicja niezmiennika. Przypomnę dla utrwalenia: żeby z niego korzystać, potrzebne są przekształcenia zbioru (dziedziny funkcji), a nie zmiany układu współrzędnych. Dla sprawdzenia czy dobrze rozumiemy tak zdefiniowane symetrie, przytoczę trochę ciekawostek.
Wyliczenia ZTS z poprzedniego podrozdziału pokazujące „zachowanie postaci q”, można teraz całkiem ściśle potraktować, jako dowód że φ nie zmienia q (kółeczko we wzorze poniżej oznacza złożenie odwzorowań):
q◦φ = q
Każde przekształcenie liniowe M możemy złożyć z trzech podstawowych działań:
- zmiana kierunku na M, czyli zamiana x → -x;
- rozciągnięcie/ściśnięcie M, czyli przeskalowanie: x → αx (dla α>0);
- przesunięcie na M, czyli x → x + β
Przeliczyliśmy już, że każde z tych „atomowych” przekształceń, generuje przekształcenie na V, które zachowuje naszą funkcję q = -Δ/(4a).
Weźmy pierwsze z nich: odbicie symetryczne M, czyli zmiana znaku x → -x. Na przestrzeni trójmianowej V objawi się ono zmianą znaku b:
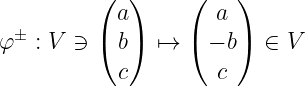
I chyba oprócz tego, że bardzo podobnie wyglądają pewne bardzo ważne symetrie w fizyce, nie da się wiele powiedzieć na jego temat.
Kolejne dwie transformacje da się sparametryzować ciągłym parametrem. I tak przeskalowania x da się przedstawić za pomocą jednoparametrowej grupy:
x → exp(s)x gdzie s∈R
Parametr s został tak dobrany, by dla wartości równej 0 dostać przekształcenie tożsamościowe na M. Działanie to przenosi się następująco na V:
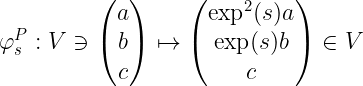
Trzecim „atomowym” przekształceniem na M, będzie przesunięcie x (s=0 również jest przypisane do jedynki grupowej):
x → x+s gdzie s∈R
Generuje ono następujące przekształcenie V:
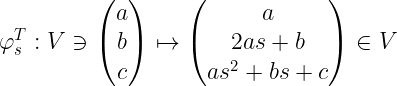
Jak już napisałem, te trzy symetrie, jako przypadki szczególne (*), zachowują funkcję q = -(b2-4ac)/4a. Sprawdzenie tego faktu metodą ZTS upewni nas, że nie pomyliśmy się w rachunkach.
Powyższe zbiory przekształceń – { φTs } oraz { φPs } – zostały tak napisane, by tworzyły grupy. Zbiór wszystkich działań, powstały przez składanie powyższych trzech podstawowych, też jest grupą, choć to może mniej widoczne. Czyli w tym przypadku przekształcenia stanowiące podstawę symetrii są grupą. W zasadzie od czasów kiedy wymyślono grupy, zaczęto je wiązać z symetriami, więc fizyk słysząc o symetrii, od razu pyta się o jaką „grupę symetrii” chodzi
Mała osobista dygresja na koniec: Czasami posługiwanie się konkretną grupą (np. wyrażoną w postaci macierzy) przesłania fizykom fakt, iż elementy tej grupy objawiają się jako przekształcenia badanego zbioru – na przykład dziedziny funkcji, których używamy do opisu danego zagadnienia. Zdałem sobie z tego sprawę, gdy studiowałem pewien podręcznik, przedstawiający jedno z ważniejszych twierdzeń w fizyce teoretycznej, o którym więcej napiszę w następnym odcinku.
* * *
Niby zwykłe równanie kwadratowe, a tyle już powypisywałem. Zatrzymam się jednak w tym szaleństwie, choć w kolejce czekają grupa ciągłych przekształceń G={ φB, φT } i jej algebra Liego. Można też zauważyć, że φB i φT są potokami na V i dzięki temu możemy znaleźć ich pola wektorowe, oraz równania różniczkowe zwyczajne zbudowane dzięki tym polom, które po rozwiązaniu odtworzą oba potoki. Można też pokazać, że funkcja q jest jedynym niezmiennikiem przekształceń (*). I pewnie coś jeszcze by się znalazło, ale pora przerwać tę, wydawałoby się, sztukę dla sztuki.
Tymczasem powyższa „praca” wcale nie jest tak beznadziejnie niepotrzebna, jakby się wydawało. Część odbytego treningu przyda się w zapowiedzianej kolejnej notce.
[1] Osobiście nie lubię tego powiedzenia, bo zachowanie postaci równań jest słabą przesłanką do uciechy. Na przykład przejście z układu kartezjańskiego na układ działanie-kąt zmienia postać równań Hamiltona, a jest bardzo przydatne.







Komentarze
Pokaż komentarze (6)