Jak to już tradycyjnie jest w mechanice kwantowej, stany kubita reprezentowane są przez wektory o długości/normie 1 w dwuwymiarowej zespolonej przestrzeni Hilberta C2. Dwuwymiarowa przestrzeń zespolona C2 jest czterowymiarową przestrzenią rzeczywistą R4, a warunek noma = 1 jest równaniem 3-wymiarowej sfery S3 w tej czterowymiarowej przestrzeni. Pisałem o tym w notce Kubitiowa 3-sfera. Sparametryzowaliśmy tę sferę trzema kątami:
X = sin (φ/2) cos ( ψ)
Y = sin (φ/2) sin ( ψ)
Z= cos (φ/2) cos ( θ+ψ)
W = cos (φ/2) sin ( θ+ψ)
Przy tym
0 ≤ φ ≤ π, 0 ≤ θ,ψ ≤ 2π
Idzie teraz o to jak tę sferę można/należy sobie wyobrazić? Jak ją przedstawić graficznie? Sferę dwuwymiarową, na przykład powierzchnię Ziemi, zwykle przedstawiamy na dwuwymiarowej płaszczyźnie przy użyciu takiej czy innej siatki kartograficznej . Można też użyć rzutu stereograficznego. I tak postąpimy w naszym przypadku. Zrzutujemy sferę S3 na R3 stereograficznie, z punktu X=Y=Z=0, W=1 na przestrzeń x,y,z rozumianą jako X,Y,Z przy W=0. By zrozumieć jak to się robi, można zajrzeć do Wikipedii pod hasło 3-sphere. Formuły są proste:
x = X/(1-W)
y = Y/(1-W)
z = Z/(1-W)
Punkt W=1, z którego rzutujemy ucieka do nieskończności. Punkt pod nim, W=-1, przechodzi w x=y=z=0. Dla punktów na równiku W=0, mamy x=X,y=Y,z=Z.
Chcemy teraz zobrazować linie współrzędnych kątowych φ,ψ,θ przez równania parametryczne
x(φ,ψ,θ ) = sin (φ/2) cos ( ψ) / (1-cos (φ/2) sin ( θ+ψ))
y(φ,ψ,θ ) = sin (φ/2) sin ( ψ) / (1-cos (φ/2) sin ( θ+ψ))
z(φ,ψ,θ ) = cos (φ/2) cos ( θ+ψ) / (1-cos (φ/2) sin ( θ+ψ))
Potrzebny nam do tego program rysujący parametryczne powierzchnie. Kiedyś, przed laty, taki program polecałem. Dziś ten dawny program (oparty na Javie) nie chce juz działać. Próbowałem wymieniony w notce o kubitowej 3-sferze program MathMod, ale też nie udało mi się nic nim namalować. Próbowałem programu Octave - też bez rezultatu. Może ktoś z czytelników coś znajdzie - mi się nie udało. Zatem opiszę jak to robię przy użyciu komercyjnego programu Mathematica. Nie znalazłem innego rozwiązania.
Najpierw wprowadzam parametryzację sfery S3:
X[theta_, phi_, psi_] = Sin[phi/2]*Cos[psi]
Y[theta_, phi_, psi_] = Sin[phi/2]*Sin[psi]
Z[theta_, phi_, psi_] = Cos[phi/2]*Cos[psi + theta]
W[theta_, phi_, psi_] = Cos[phi/2]*Sin[psi + theta]
Rysuję parametrycznie trzy powierzcnie kątów theta i psi przy ustalonym phi równym kolejno Pi/4, Pi/2, 3 Pi/4:
p1 = ParametricPlot3D[{X[theta, Pi/4, psi]/(1 - W[theta, Pi/4, psi]),
Y[theta, Pi/4, psi]/(1 - W[theta, Pi/4, psi]),
Z[theta, Pi/4, psi]/(1 - W[theta, Pi/4, psi])}, {psi, 0,
2 Pi}, {theta, 0, 2 Pi},
PlotRange -> {{-2.5, 2.5}, {-2.5, 2.5}, {-1.3, 1.3}},
Mesh -> {0, 20}, PlotStyle -> {Orange, Specularity[White, 10]},
PlotPoints -> 50]
p2 = ParametricPlot3D[{X[theta, Pi/2, psi]/(1 - W[theta, Pi/2, psi]),
Y[theta, Pi/2, psi]/(1 - W[theta, Pi/2, psi]),
Z[theta, Pi/2, psi]/(1 - W[theta, Pi/2, psi])}, {psi, 0,
3 Pi/2}, {theta, 0, 2 Pi},
PlotRange -> {{-2.5, 2.5}, {-2.5, 2.5}, {-1.3, 1.3}},
Mesh -> {0, 20}, PlotStyle -> {Orange, Specularity[White, 10]},
PlotPoints -> 50]
p3 = ParametricPlot3D[{X[theta, 3 Pi/4,
psi]/(1 - W[theta, 3 Pi/4, psi]),
Y[theta, 3 Pi/4, psi]/(1 - W[theta, 3 Pi/4, psi]),
Z[theta, 3 Pi/4, psi]/(1 - W[theta, 3 Pi/4, psi])}, {psi, 0,
2 Pi}, {theta, 0, 2 Pi},
PlotRange -> {{-2.5, 2.5}, {-2.5, 2.5}, {-1.3, 1.3}},
Mesh -> {0, 20}, PlotStyle -> {Orange, Specularity[White, 10]},
PlotPoints -> 50]
I pokazuję wszystkie trzy powierzchnie razem
q1 = Show[{p1, p2, p3}, Background -> Black]
Powstaje taki obrazek
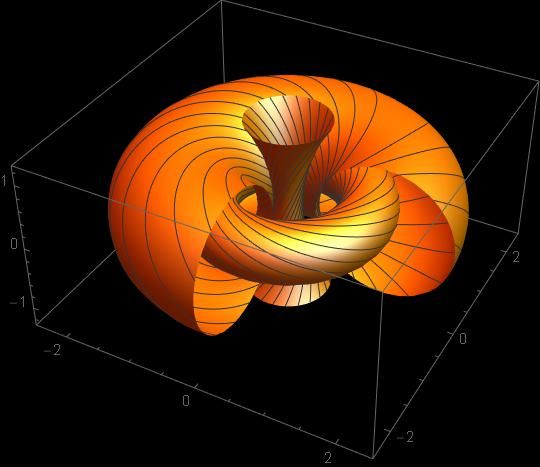
Widoczne są linie parametru psi. Teraz trzeba zaprzęgnąć wyobraźnię. Ta pionowa trąbka, to kawałek OGROMNEGO torusa. Zamyka się gdzieś poza obrębem układu słonecznego :)
Kąt psi okaże się ważny - "kwantowa faza". Ale o tym w kolejnej notce.
W międzyczasie w moich notkach była nierównomierność. Pracowałem nad poprawianiem błędów w mojej pracy o algebrach Clifforda (gdzie też pojawia się coś w rodzaju kwantowej fazy). Wczoraj ukończyłem to poprawianie i dziś już jest dostępna nowa wersja:
https://arxiv.org/abs/2103.09767
P.A. Ale się rąbnąłem! Po komentarzu Tichego narysowałem całą trąbke. I okazało się, że mieści się w zakresie (-5,5) , podczas gdy obrazek trzech torusów był w (-2.5,2.5):
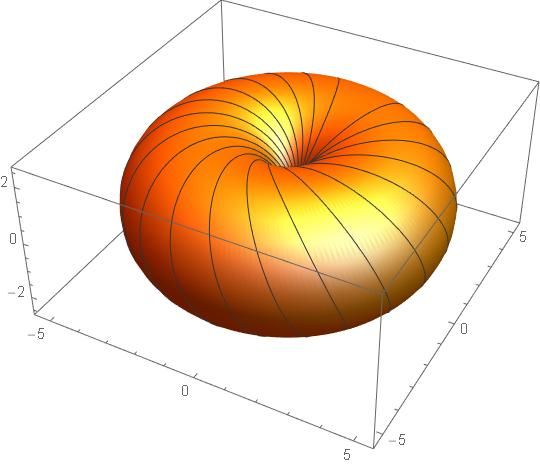
A tu dodałem linie parametru theta:
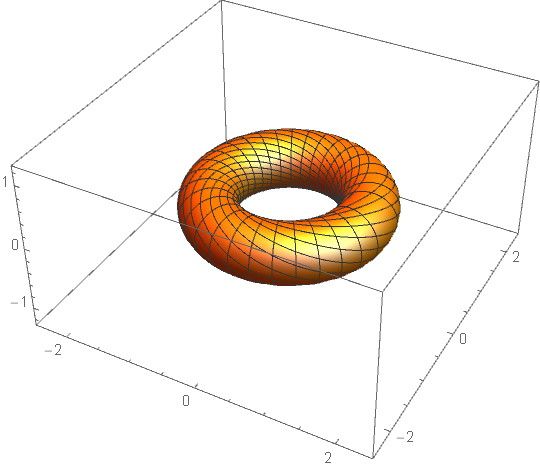







Komentarze
Pokaż komentarze (39)