Dzisiaj żadnej mistyki, żadnej ezoteryki nie będzie. Możesz odetchnąć z ulgą drogi Czytelniku. Nie będzie też kół czy okręgów. Koła, półkola, to z architektury romańskiej. A my wrócimy do gotyku, jako, że strzeliste wieże służą zapewne czemuś wzniosłemu choć stojącemu solidnie na ziemi. A czemu? Zostawmy to pytanie na koniec tej noty.
Ostatnim razem poznaliśmy drzewo Fareya. Wiemy jak porozmieszczać liczby wymierne po poziomach podziemnego drzewa. Oto poziomy +1, 0, -1, -2.
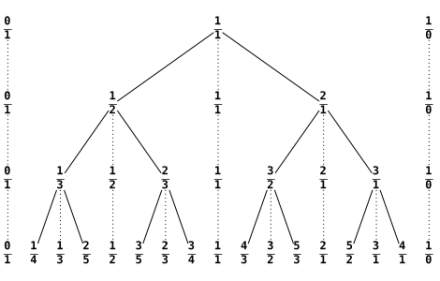
Czym dalej w głąb, tym więcej liczb wymiernych na danym poziomie. Zajmiemy się dziś tylko lewą gałęzią drzewa, liczbami mniejszymi od jedności. Na poziomie zerowym – jedna liczba. Na poziomie -1 dwie liczby, na poziomie -2 cztery liczby. Nietrudno się domyślić, że na poziomie -k będzie 2k liczb. Z każdym następnym poziomem liczba zamieszkujących na nim liczb będzie się podwajać. W szkole czasami uczą wzoru na postęp geometryczny. Możemy z tego wzoru skorzystać, by się przekonać o tym, że na poziomach od 0 do -k mieszka łącznie 1+2+ ... +2k = 2k+1-1 liczb. Zajmiemy się dziś liczbami zamieszkującymi do poziomu szesnastego włącznie. Czemu akurat szesnastego? Bo mój komputer je obrabia wciąż jeszcze w rozsądnym czasie. Ze wzoru powyżej łatwo znajdziemy, że nasza populacja liczy sobie 217-1 = 131071 liczb. Niezłe miasteczko. Właściwie nawet miasto. Nadaje się do badań statystycznych.
Zadanie, które stawiamy jest proste: mamy do zbadania ponad sto tysięcy liczb wymiernych pomiędzy zerem a jedynką. Podzielmy więc odcinek między zerem a jedynką na N równych przedziałów, powiedzmy, że jest to przedział dochodów, pomiędzy 0 – żadnych dochodów, a 1 – maksymalny dochód danego gospodarstwa domowego. Ile liczb z naszej populacji będzie się mieściło w każdym z wybranych przedziałów. Pojawia się pytanie ile tych przedziałów wybrać? Chodzi zawsze o to, by tak dobrać ilość przedziałów, by było ich ani za mało ani za dużo. Jeśli będzie ich za mało, możemy przegapić istotne prawidłowości. Jeśli będzie ich za dużo, tez możemy prawidłowości przegapić, bo utoniemy w szczegółach. Nie ma np sensu tworzenie nowego przedziału co złotówkę. Zawodowi statystycy maja zapewne swoje wypracowane metody. Dla nas metodą będą możliwości wizualne ekranu komputera. Aby umieścić obrazek na blogu, muszę ograniczyć się do 440 pikseli szerokości. No, zawsze mogę utworzyć obrazek w większej rozdzielczości i go przeskalować. Ale przy skalowaniu można stracić ważne szczegóły. Końskim targiem podzieliłem odcinek pomiędzy zerem a jedynką na 600 przedziałów i zliczyłem procent populacji (131071 liczb) mieszczący się w danym przedziale. Zrobiłem grafik łącząc kolejne punkty linią łamaną. Myślicie może, że wyszła znana wszystkim ze statystyk krzywa dzwonowa? Maksimum w środku?
Tak myślicie? No to mamy niespodziankę:
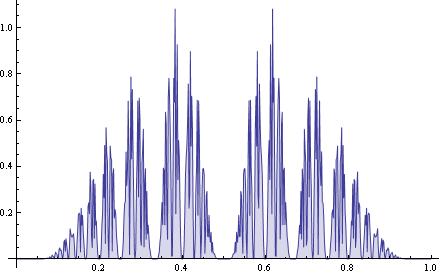
Nasze liczby najwyraźniej unikają zarówno skrajności jak i przeciętności. Wyraźnie szukają „złotego środka” a nie tego pospolitego.
Zaraz, zaraz..... Już kiedyś cos podobnego widziałem.... Francuski fizyk Jean-Marie Souriau, autor znanej monografii „Structure of Dynamical Systems. A Symplectic View of Physics”, współtwórca metody „kwantowania geometrycznego, dziś człowiek już wiekowy, u którego w domu w Aix-en-Provence kiedyś nawet byłem, miód i wino piłem, miał podobny wykres w swojej pracy spekulującej nad prawidłowościami orbit planet w Układzie Słonecznym. Tyle, że dostał go zupełnie inną metodą. Oto ten wykres z pracy Souriau:
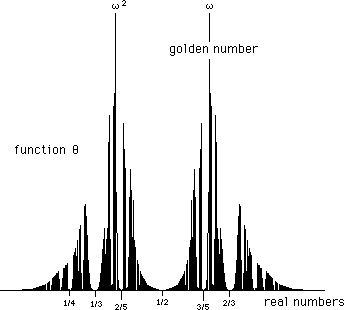
Dokładnie taki sam? Niezupełnie. Jednak nasze oko wyczuwa, że prawidłowość jest ta sama. Piki i minima są podobnie porozkładane!
Będąc ciekawymi zastanawiamy się: jak to podobieństwo wyjaśnić? Sam Souriau wspominał coś o teorii liczb, wymieniał matematyków Borela, Lagrange'a, Hurwitza, Liouville'a ..., ale daleki był od precyzji. Nie raczył był nawet wyjaśnić jak konkretnie swój wykres otrzymał. Gorzej: nie raczył był nawet opublikować swej pracy – zrobił to za niego jego uczeń, Jean-Pierre Petit. I to tylko w internecie! Nagabywani przeze mnie zawodowi matematycy od teorii liczb kręcili tylko głowami: „no, nie wiem....”
A jednak jest ktoś, kto może wiedzieć jaki jest związek pomiędzy jednym wykresem a drugim. Ktoś, kto potrafi odtworzyć tajemniczą metodę Souriau i znacznie znacznie więcej. Ktoś, kto zasługuje na zapis w historii co najmniej tak jak Farey i Ford.
Co więcej, ten ktoś pisze i komentuje w Salonie24. Zgadnijcie kto?
Wskazówka: o, nie, ten ktoś nie jest bynajmniej fizykiem.








Komentarze
Pokaż komentarze (67)