Badania modeli w żadnym tunelu aerodynamicznym, zatem także w Wojskowej Akademii Technicznej ani na uniwersytecie w Akron, nie dostarczą informacji potrzebnej by odtworzyć przebieg obrotu tupolewa PLF 101 w dniu 10.04.10 w Smoleńsku. Powodem tego jest poważne naruszenie praw skalowania i brak możliwości pomiarów na szybko obracającym się modelu w tunelach aerodynamicznych. Podkomisja Macierewicza probuje modelować lot albatrosa przy użyciu kolibra, a obroty młyna dmuchając na jego miniaturkę unieruchomioną w imadle. (Albatros nie lata tak jak koliber nie dlatego, że przyroda nie wpadła na pomysł zmniejszenia albatrosa lub powiększenia kolibra, tylko dlatego, że powietrze oddziałuje inaczej z obiektami o tak różnej wielkości, co wymaga innego rodzaju skrzydeł.) Na szczęście wszystkie drogie skany tupolewa i badania w tunelach nie są nikomu potrzebne, gdyż trajektoria tupolewa jest już od dawna dobrze poznana i obliczona.
ZLECENIE
Badania w tunelach aerodynamicznych zleciła podkomisja Macierewicza z MON, prowadzona po niesłychanie gwałtownym wyjeździe z Polski blogera s24 Berczyńskiego (dr. Wacława Berczyńskiego)[1] przez blogera KaNo (dr. Kazimierza Nowaczyka). Ten drugi wyprowadził się z salonu24 w pewnym związku z pracami niżej podpisanego. Można podejrzewać, że ważną rolę w tym zamówieniu odegrał też jeszcze jeden dawny bywalec s24 (Marek Dąbrowski), przewodniczący sekcji lotnictwa (!) w tej dziwnej, nieprofesjonalej "podkomisji" państwowej. Dlatego wypada, by bezsens prowadzonych za miliony złotych badań wykazał także autor salonu24, you know who. Wykonawcami ważnego dla polskiej racji stanu zadania są: ludzie prof. Wiesława Bieniedy w Akron oraz nie znani mi bliżej inżynierowie WAT w Warszawie. Notka będzie krótka i prosta, po to by nie tylko czytelnicy salonu, ale przede wszystkim podkomisarze mogli ją w 100% zrozumieć przed planowanym zebraniem 17.05.17 w klubie WAT. W przypadku niejasności, zapraszam przedstawicieli

do University of Toronto na prowadzone przeze mnie okresowo wykłady dla studentów ostatniego roku studiów z aerodynamiki płatowca.
PROBLEM nr 1: SKALOWANIE AERODYNAMICZNE, TURBULENCJA I LICZBA REYNOLDSA
Ponieważ obiecałem krótką notkę, po długie i wyczerpujące opowieści o tych ciekawych zagadnieniach odsyłam do licznych książek w rodz. 0 bloga i www.internet.com
Zacznijmy od turbulencji powietrza. W napływającym na samolot powietrzu byla niewielka, co jest typowe dla takich warunków meteo: stratus, gęsta mgła, mały wiatr 3 m/s. Jeśli chodzi o turbulencję generowaną na skrzydle, to teorie Prandtla i Schlichtinga pozwalają ocenić największą grubość warstwy granicznej (turbulentnej) na kilka cm, i to na samym końcu skrzydła TU-154M. Natomiast w ośrodku opływającym modele w skali 1:100 (lub podobnej), turbulencja była odtworzona bardzo źle. Na licznych kadrach "strasznego filmu" pokazanego przez podkomisję w dniu 10.04.17 w WAT[2], na przykład na Rys. 1 widzimy, że potok napływający, gdyby przeskalować go do realnego świata, zawierałby komórki turbulentne o rozmiarach R~2/3 m, rotujące na odległości przepływu ~2m, czyli w okresem rotacji około R/U~0.01 s (U ~ 75 m/s to prędkość napływu). To byłaby nierealna prędkość turbulentna odpowiadająca ponad 100 km/h. O tym co się dzieje w przepływie nad skrzydłem modelu lepiej zamilczeć... to tragicznie smutna historia wynikająca z błędnej skali modelu i niedoskonałości urządzenia. W rzeczywistości już ~10 cm nad skrzydłem przepływ jest laminarny (~1 mm w skali modelu).
Rys.1 
Nawiasem mówiąc, systematycznie nierówna prędkość przepływu w różnych miejscach przekroju poprzecznego tunelu/kanału, nadmierna turbulencja napływającego ośrodka, efekty pobliskich ścian tunelu silnie modyfikujące wyniki, to typowe problemy omawiane w literaturze fachowej [13]; nie jest to więc trudność występująca tylko w omawianych badaniach, czy tylko w tunelach wodnych.
Jeśli chodzi o liczbę Reynoldsa (Re), to jest to bezwymiarowy wskaźnik ważności efektów inercjalnych w porównaniu z efektami lepkości ośrodka. Taki miernik odwrotności lepkości. W hydro- i aerodynamice dwa przepływy cieczy lub gazu nie są zawyczaj podobne do siebie i nie można używać jedego jako dobrego analogu drugiego, jeśli liczba Re rożni się w tych przepływach o czynnik 10, 100, lub więcej. Można bowiem dostać zasadniczo różne zjawiska i wyniki nie mające nic wspólnego z modelowaną sytuacją. Np. współczynnik siły nośnej danego ciała może różnić się dość znacznie, a współczynnik oporu nawet wielokrotnie, gdyż rodzaj opływu (pole wektorowe prędkości), różnić się mogą zasadniczo. Tak niestety stało się w obecnych próbach modelowania tupolewa.
Re = L U /v,
gdzie L = rozmiar obiektu opływanego, U jest prędkością napływającego powietrza (U = 70-80 m/s), zaś ν (greckie "nu") to wpółczynnik lepkości kinematycznej powietrza ν = 1.4e-5 m^2/s.
W przypadku samolotu TU-154M jako całości to w przybliżeniu L = 40 m, a samego jego skrzydła to 4 m (typowa cięciwa skrzydła), zatem Re(samolot) ~ 200 mln, a dla Re(skrzydła) ~ 20 milionów.
Badane modele były mniej więcej w skali 1:100 (niektóre 1:50). Szybkość przepływu U w zastosowanych tunelach aerodynamicznych, a zwłaszcza w hydrodynamicznym, nie przekraczała 40 m/s (zaś 20 m/s w wiekszej średnicy tunelu 1.1m gdzie wstawiono metrowy model), tzn. około 1/2 (wzgl. 1/4) smoleńskiej wartości U~75 m/s. Zatem w przybliżeniu liczba Reynoldsa była w tunelach ~200 razy za mała w stosunku do realnej (przy płacie głównym wynosiła w modelach nie więcej niż 100000 do 130000, czyli była "bardzo mała"; zob. cytat [13] i uwagę [14]).
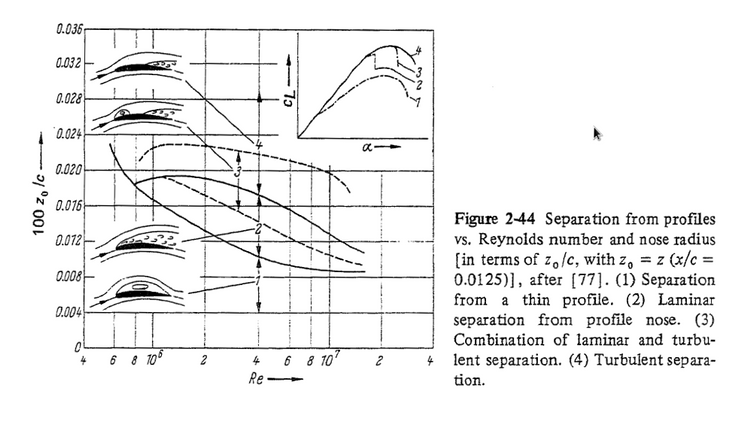
Do czego to może prowadzić? Do błędnego rodzaju opływu powietrza wokół powierzchni nośnych modelu, złych mierzonych wartości sił i ich momentów. Spójrzmy na Rys. 2 z klasycznej książki Schlichtinga i Truckenbrodta[3]. Zilustrowano różne (zależne od stosunku grubości skrzydła z0 w odległości 1/80 cięciwy "c" od krawędzi natarcia; z0/c jest proporcjonalne do promienia krzywizny krawędzi natarcia) mody odrywania się strugi od skrzydła: symbolem 1 oznaczono zakres z0/c pod krzywą ciągłą opisującą cienkie profile, gdzie oderwanie ma charakter recyrkulacji, symbolem 2 zakres oderwania laminarnego strugi, symbolem 3 połączenie oderwania laminarnego i turbulentnego, a symbolem 4 oderwanie w pełni turbulentne. Pokazane są też w prawym górnym rogu schematy zależności wsp. siły nośnej CL od kąta natarcia α, warto zwrócić uwagę na duży spadek siły nośnej np. w reżimie 1 i 2. Na osi poziomej zaznaczona jest na osi logarytmicznej liczba Reynoldsa, w zakresie or 0.4 do 40 milionów, wartości skrajne są bliskie liczbom Reynoldsa skrzydła tupolewa, odpowiednio: w tunelu UA/WAT, oraz w rzeczywistości smoleńskiej. z0/c wynosi ~0.02 na profilu skrzydła i slatu przedniego tupolewa. Zatem rzeczywisty tupolew ma opływ i zerwanie strumienia typu 4 (wytwarzające największą siłę nośną), natomiast w skali 1:100 będzie miał zupełnie nierealistyczne zerwanie i recyrkulację strumienia typu 1. Model będzie się cechował znacznie mniejszym CL i wyliczoną z niego siłą nośną, będzie też naturalnie miał inną czułość na wychylenie powierzchni kontrolnych.
Rys. 2
Zmierzone w tunelu aerodynamicznym zależności współczynników siły nośnej CL i oporu Cd dla profilu aerodynamicznego NACA 2412 o podobnej grubości względnej do zastosowanego w TU-154M, pokazuje Rys.3. Widać na nim wyrażnie, że w siła oporu zależy znacznie od Re. Siła nośna zależy od liczby Reynoldsa przy dużych kątach natarcia α (alfa), takich jakie występowały pod koniec tragicznego lotu PLF 101. Jak wspomniałem, w tunelach studenckich i małoskalowych (średnica do ok. 1 m) zmierzymy za małą bezwymiarową siłe nośną. Gdy WAT pokaże wykresy CL(AOA) stanie się jasne, czy to przewidywanie jest słuszne.
Rys. 3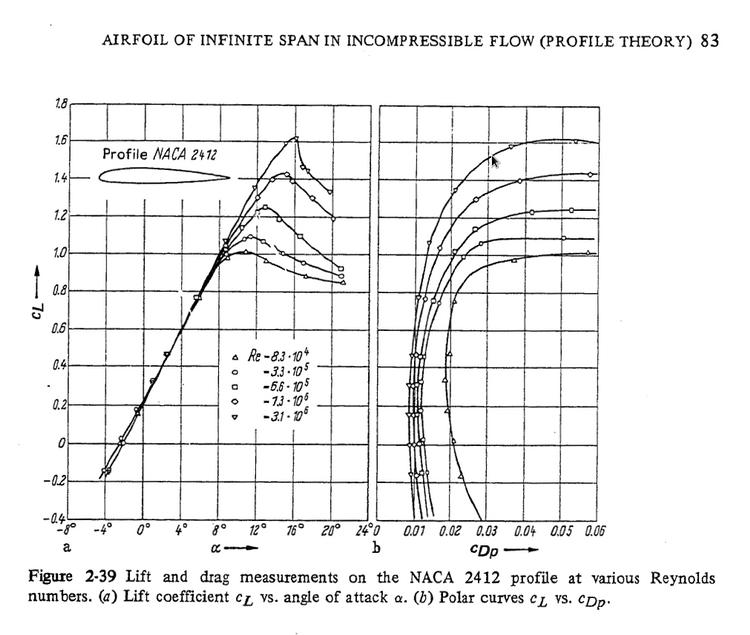
Rysunek 4 pokazuje wyniki pomiarów CL_max uzyskiwanych z ośmiu opisanych symbolami rodzajów przekroju płata z serii "6" NACA. Eksperymenty pokazują średnio 40-procentową redukcję maksymalnego współczynnika siły nośnej przy zaledwie 20-krotnej redukcji liczby Re (dużo mniejszej, niż o czynnik 200 między realiami smoleńskimi a macierewiczowskimi badaniami). Jak źle wyznaczone są statyczne współczynniki aerodynamiczne w modelach 1:100? Zapewne mają ponad 50% błędu. Nie jest też jasne czy poprawnie odtwarzają zerwanie strugi przy przeciągnięciu.
Rys. 4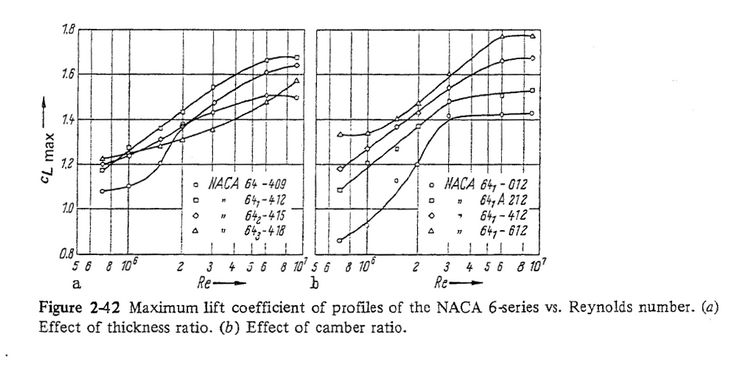
PROBLEM nr 2: LOTU TU-154M PO UTRACIE KOŃCÓWKI SKRZYDŁA NIE UDAŁO SIĘ I NIE UDA NIGDY WYMODELOWAĆ FIZYCZNIE
Pokażę, że to, co proponuje nam podkomisja to badania modelowe pracy młyna na nieobracajacym się modelu o wielkości 10 cm. Można tak próbować ilustrować, że młyn zechce się kręcić na wietrze (w przypadku smoleńskim: wyznaczyć moment siły po urwaniu części skrzydła i pokazać, że samolot stał się niesterowny), ale na pewno nie z jaką prędkością i okresem obrotu będzie się młyn obracał na zmiennym wietrze.
O ile problem nr 1 jest trudny do rozwiązania, ale przynajmniej teoretycznie jest jeszcze na świecie parę wielkich tuneli aerodynamicznych, gdzie można by zakupić dostęp, zbudować dużo większy model (5m) i spróbować wyznaczyć przy sensowniejszej liczbie Re współczynniki statyczne (CL, Mx, CLa, ...), o tyle problem nr 2 jest beznadziejny. Nie ma rozwiązania technicznego, ponieważ w tunelach aerodynamicznych bada się przepływy ustalone w strumieniu, ktory nie wiruje. Natomiast ostatnie 6 sekund lotu tupolewa to typowy problem przepływu nieustalonego, gdzie wszystkie kąty szybko zmieniają się w czasie, a rodzaj opływu w 3 wymiarach jest zupełnie inny, niż w przypadku przepływu ustalonego (gdzie model jest w imadle tensometrycznym, na linach, stelażu, itp.). To nie jest wcale drobna różnica - to jest istota faktycznej beczki smoleńskiej i wytłumaczenie bardzo dobrze znanej historii obrotu: samolot wykosił w drzewach dobrze znaną spiralę, której bez opisanego niżej efektu absolutnie nie da się wyjaśnić ilościowo [4][5][6][7][8]. Odwołam się znów do rysunku zacnego Schlichtinga (świetnego aerodynamika i odkrywcy, ale i jak widać też dobrego pedagoga)[3]. Rys. 5 pokazuje zasadniczą zmianę w aerodynamice obracającego się płata skośnego, takiego jak skrzydło tupolewa (zilustrowany jest płat symetryczny, ma kompletne lewe skrzydło).
Rys. 5
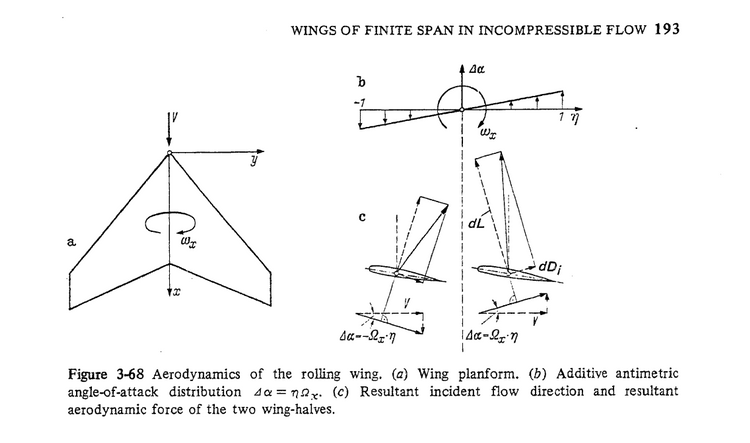
Samolot obraca się na rysunku z prędkością kątową ωx. Jedno skrzydło opada, drugie się podnosi. Prędkość tego ruchu jest antysymetryczną funkcją współrzędnej y (lub bezwymiarowej η); linowe prędkości ruchu końcówek są równe połowie rozpiętości płata razy prędkość kątowa. W Smoleńsku TU-154M obrócił się prawie do góry kołami (o 145 st.) w czasie ~4.5 s po utracie końcowki skrzydła. Średnio obracał się 145 st/4.5s = 32 st/s, ale po ~2 sekundach od urwania skrzydła dużo szybciej niż ta średnia, maksymalnie do ωx = 48 stopni/s [10]:
Rys. 6
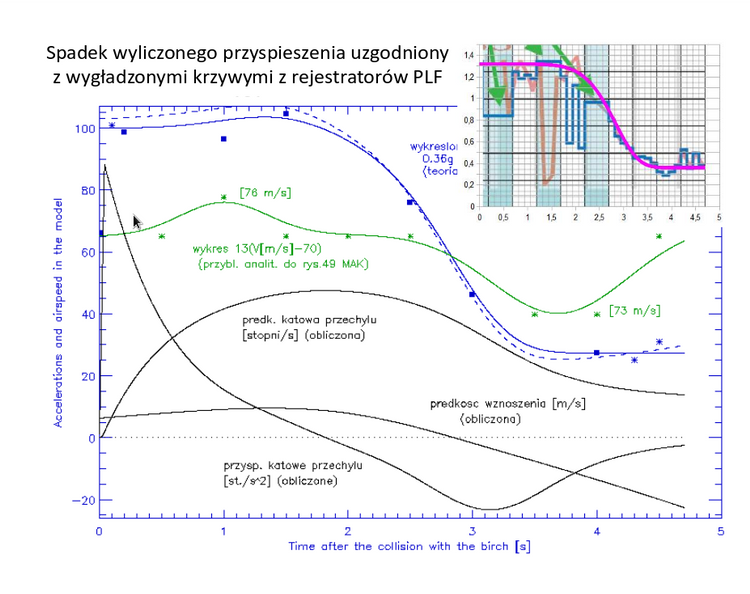 Przez całe dwie sekundy, ωx~ 40 st/s lub więcej. Lewy kikut był ~13 m od osi obrotu, a prawa końcowka skrzydła ~18 m od niej. Względem samolotu te punktu poruszały się więc prostopadle do skrzydła z prędkościami równymi co najmniej, odpowiednio, -9 i +12.6 m/s. To, jak zaznaczono trójkątami prędkości na Rys. 5, kompletnie zmieniło kąty natarcia w okresie rozkręconego obrotu, o ponad +9/75 rad = +6.9 stopni na lewym skrzydle, oraz -12.6/75 rad = -9.6 stopnia na prawej końcówce skrzydła, sumarycznie aż o ponad 16 stopni. A to z kolei powodowało bardzo znaczną różnicę CL i sił nośnych. W efekcie pojawił się moment siły, który oganiczył przyrost i w końcu nawet spowolnił obrót wywołany dużą asymetrią płata; por. powyższy wykres prędkości kątowej przechyłu ωx(t). Asymetria płata oczywiście ciągle była, ale kąty natarcia niezwiązane z obrotem spadły po paru sekundach - obrót w końcu zwolnił do trzy razy wolniejszego niż maksymalne ωx. Trajektoria w 3 wymiarach, również wszystkie kąty przycięcia drzew, daje się odtworzyć tylko pod warunkiem uwzględnienia wpływu szybkiego obrotu na dynamikę samolotu. Tego nie udało się i nie uda zrobić doświadczalnie, poza być może paroma miejscami na świecie. Powód jest prosty.
Przez całe dwie sekundy, ωx~ 40 st/s lub więcej. Lewy kikut był ~13 m od osi obrotu, a prawa końcowka skrzydła ~18 m od niej. Względem samolotu te punktu poruszały się więc prostopadle do skrzydła z prędkościami równymi co najmniej, odpowiednio, -9 i +12.6 m/s. To, jak zaznaczono trójkątami prędkości na Rys. 5, kompletnie zmieniło kąty natarcia w okresie rozkręconego obrotu, o ponad +9/75 rad = +6.9 stopni na lewym skrzydle, oraz -12.6/75 rad = -9.6 stopnia na prawej końcówce skrzydła, sumarycznie aż o ponad 16 stopni. A to z kolei powodowało bardzo znaczną różnicę CL i sił nośnych. W efekcie pojawił się moment siły, który oganiczył przyrost i w końcu nawet spowolnił obrót wywołany dużą asymetrią płata; por. powyższy wykres prędkości kątowej przechyłu ωx(t). Asymetria płata oczywiście ciągle była, ale kąty natarcia niezwiązane z obrotem spadły po paru sekundach - obrót w końcu zwolnił do trzy razy wolniejszego niż maksymalne ωx. Trajektoria w 3 wymiarach, również wszystkie kąty przycięcia drzew, daje się odtworzyć tylko pod warunkiem uwzględnienia wpływu szybkiego obrotu na dynamikę samolotu. Tego nie udało się i nie uda zrobić doświadczalnie, poza być może paroma miejscami na świecie. Powód jest prosty.
Aby odtworzyć właściwe, bardzo różne kąty natarcia na lewym i prawym skrzydle (a także statecznikach) trzeba, aby model leciał względem powietrza po spirali takiej jak prawdziwa, tzn. by w czasie obrotu samolot i model przeleciały tyle samo swych długości (samolot ~330 m, czyli ponad 6 swych 50-metrowych długości, a model 330 cm, czyli tyle samo swych 50-centymetrowych długości). W średniej wielkości tunelu IL albo WAT powietrze leci ok. 40 m/s, a to wymagałoby obrotu modelu o 145 stopni (0.4 pełnego obrotu) w całkowitym czasie zaledwie T = 83ms. Innymi słowy, model powinien się obracać średnio pięć razy na sekundę, a w porywach do 10 razy, czyli 600 rpm! To praktycznie niewykonalne, by przy tym mierzyć poprawnie siły aerodynamiczne. Jedynie bardzo specyficznie zbudowany, wyważony i zdalnie kierowany, ale niemal swobodnie lecący w wielkim tunelu aerodynamicznym model TU-154M mógłby pozwolić zmierzyć empirycznie współczynniki aerodynamiczne, ich pochodne i momenty sił w stanie nieustalonym. Te wielkości zostały koncepcyjnie źle zrozumiane i nie za dobrze pomierzone w Warszawie[15], a tym bardziej w Akron, gdzie po 7 latach kąty wznoszenia, natarcia i pochylenia bywają ciągle jeszcze mylone.
PODKOMISJA, CZYLI JEDNO WIELKIE NIEPOROZUMIENIE
Najlepszy przykład: podkomisarze polecili mierzyć w WAT umocowane na sztywno modele obrócone do góry kołami tak, że widać wyraźnie na ich filmie[2], że kąt natarcia jest ujemny (por. 28:07)!

Rys. 7
Po co? Czegoś takiego nie było w locie PLF101, bo gdyby było, to zapisałoby się jako ujemne przeciążenie w skrzynkach ATM QAR i MSRP64. W filmie[2] jest zresztą takie multum niefizycznych rzeczy, że potrzebna byłaby na nie cała osobna notka. Ale czyż warto recenzować animacje fantasy, gdzie końcowka skrzydła bije rekordy niefizyczności lotu znane z "lotu 12m" Biniendy, samolot przelatuje nad al. Kutuzowa prawie nieprzechylony, po czy wyprawia niezłe harce w powietrzu, a w końcu spadając już i tak na ziemię samolot eksploduje wysadzony termobarycznie telefonem komórkowym[11], po czym dźwięk wybuchu okazuje się wolniejszy od jego siły[12]?
___________________________
PRZYPISY
[1] - Powodem ewakuacji Berczyńskiego były wypowiedzi w wywiadzie, w ktorym o caracalch było rzucone jedno zdanie, a tyle samo lub więcej było o tym, że może rozmawiać z każdym tylko nie z autorem tej notki, gdyż ten jakoby "kłamie w sprawie smoleńskiej wiedząc o tym". Jest to nie tylko masło maślane, bo nikomu na świecie nie udało się do tej pory skłamać nie wiedząc o tym, ale także rzucanie bezzasadnych oskarżeń.
[2] - https://www.youtube.com/watch?v=dVDea7N-TR0
[3] - Hermann Schlichting, Erich Truckenbrodt, 1979, Aerodynamics of the airplane, McGraw-Hill, 542 str.
[4] - http://fizyka-smolenska.salon24.pl/444486,30-aerodynamika-beczki-smolenskiej-najprosciej-jak-mozna
[5] - http://fizyka-smolenska.salon24.pl/471834,32-nie-ma-nic-praktyczniejszego-niz-dobra-teoria
[6] - http://fizyka-smolenska.salon24.pl/474836,33-jak-tupolew-oral-ziemie-ogonem-i-jak-doznawal-slizgu,2
[7] - https://www.youtube.com/watch?v=M8yyDrR1D9Q
[8] - https://www.youtube.com/watch?v=qqQZ-846J5s
[9] - Nota bene, kiedyś po ang. pisano logiczniej, jak na rys. 5 : antimetric, teraz mówi się antisymmetric, co faktycznie po grecku oznacza: przeciwwspółmierny.
[10] - http://planets.utsc.utoronto.ca/~pawel/MechAvXVI-1.pdf
[11] - odpowiedź W. Berczyńskiego na pytanie jak konkretnie była odpalona jego "bomba termobaryczna"
[12] - odpowiedź prof. muz. A. Gruszczyńskiej na pytanie dlaczego nie słychać w CVR wybuchu (mimo tego, że zawsze de facto NTSB słyszało.. por. Czarno na Białym TVN24, red. Świerczek, 14.04.17).
[13] - J. B. Barlow, W. H. Rae, A. Pope, 1999, Low-speed wind tunnel testing, 3rd ed, J. Wiley & Sons, Inc., 713 str.
Barlow et al. piszą między innymi: "At very low values of the Reynolds number, about 150,000, the lift curve again steepens, and dCL/da may then exceed 2pi/radian", co wyraźnie wskazuje że Re ~ 100000 w WAT nie jest właściwe. Dają wiele porad teoretycznych (jakie ekstrapolacje stosować, jak korygować wyniki dla wyeliminowania tzw. zjaw (ściany tunelu zaginają przepływ tak, jakby model leciał w otoczeniu jakichś nie istniejących innych ciał zaburzających przepływ powietrza), jak i porad praktycznych (mierzyć charakterystyki aero raz w położeniu normalnym a raz odwróconym do góry kołami, przy tych samych kątach natarcia - tylko w teorii wyniki są takie same!). Autorzy podkreślają zasadnicze znaczenie Re przy używaniu tuneli aerodynamicznych. "The lower boundary for testing airfoils and wings for vehicles that will operate at higher full scale values is a Reynolds number in the range of 1,000,00-1,500,000 based on chord" (str. 63). Po polsku: "Najniższą granicą dla testowania płatów i skrzydeł w pojazdach operujących w wyższym zakresie Re w pełnej skali jest wartość 1.000.000 do 1.500.000, wyliczona w oparciu o cięciwę skrzydła". To wymaga czterometrowej wielkości modelu tupolewa w strumieniu powietrza lecącym 40 m/s. Dodam, że nie można poprawić wartości Re przez dużo większą prędkość przepływu ośrodka w tunelu aerodynamicznym, ponieważ liczba Macha 0.2 jest już prawie realistyczna, a każda większa wywołałaby silne efekty ściśliwości powietrza, nie występujące przy podejściu do lądowania.
[14] - Co prawda lepkość kinematyczna wody jest 14 razy mniejsza niż powietrza (rys. 1 jest przypuszczalnie z tunelu wodnego), co zbliża liczbę Re do realnej, ale prędkości wody są mniejsze, co oddala Re od pożądanej wartości. Ilościowych badań aeronautycznych nie robi się w kanałach wodnych.
[15] - A. Pope, 2009, Basic Wing and Airfoil Theory, Dover.str.
Ostatnie podrozdziały 13.3 i 13.4 noszą tytuły Solid Round Boundaries i Open Round Boundaries, str. 206-267. Autor opisuje tam poprawki konieczne przy opracowaniu wyników z tunelu aerodynamicznego, ze wzgl. na bliskość ścian tunelu. Robi się je dla małego płata w dużej rurze tunelu. Poprawki są praktycznie niemożliwe do wyznaczenia w przypadku, kiedy płat zajmuje prawie całą średnicę tunelu, co było widać na kadrach filmu[2] o eksperymentach w Warszawie. To poddaje w watpliwość dokładność wyników uzyskanych w WAT.

Nazywam się Paweł Artymowicz, ale wolę tu występować jako YKW. Moje wyniki zatwierdził w 2018 r. i podał za wzór W. Biniendzie jako wiarygodne wódz J. Kaczyński (naprawdę! oto link). Latam wzdłuż i wszerz kontynentu amerykańskiego (link do mapki), w 2019 r. 40 godz. za sterami, ok. 10 tys. km; Jestem niezłym (link), szeroko cytowanym profesorem fizyki i astrofizyki [link] (zestawienie ze znanymi osobami poniżej). Kilka krajów nadało mi najwyższe stopnie naukowe. Ale cóż, że byłem stypendystą Hubble'a (prestiżowa pozycja fundowana przez NASA) jeśli nie umiałbym nic policzyć i rozwikłać części "zagadki smoleńskiej". To co mówię i liczę wybroni się samo. Nie mieszam się do polityki, ale gdy polityka zaczyna gwałcić fizykę, a na dodatek moje ulubione hobby - latanie, to bronię tych drugich, obnażając różne obrażające je teorie z zakresu "fizyki smoleńskiej". Zwracam się do was per "drogi nicku" lub per pan/pani jeśli się podpisujecie nazwiskiem. Zapraszam do obejrzenia wywiadów i felietonów w artykule biograficznym wiki. Uzupełnienie o wskaźnikach naukowych w 2014 (za Google Scholar): Mam wysoki indeks Hirscha h=30, i10=41, oraz ponad 4 razy więcej cytowań na pracę niż średnia w mojej dziedzinie - fizyce. Moja liczba cytowań to ponad 4100 [obecnie 7500+, h=35]. Dla porównania, prof. Binienda miał wtedy dużo niższy wskaźnik h=14, 900 cytowań oraz 1.2 razy średnią liczbę cytowań na pracę w dziedzinie inżynierii. Inni zamachiści (Nowaczyk, Berczyński, Szuladzinski, Rońda i in. 'profesorowie') są kompletnie nieznaczący w nauce/inż. Częściowe archiwum: http://fizyka-smolenska.blogspot.com. Prowadziłem też blog http://pawelartymowicz.natemat.pl.
Nowości od blogera
Inne tematy w dziale Polityka

