Poproszono mnie o rozwiązanie następującego zadania z ostatniego etapu olimpiady matematycznej dla szkół podstawowych: w trapezie prostokątnym podstawy mają długości 2 cm i 8 cm, a wysokość 8 cm. Oblicz odległość punktu przecięcia przekątnych od krótszej podstawy wiedząc, że odległość tego punktu od dłuższego ramienia wynosi 1,3 cm.
Wygląda to mniej więcej tak:
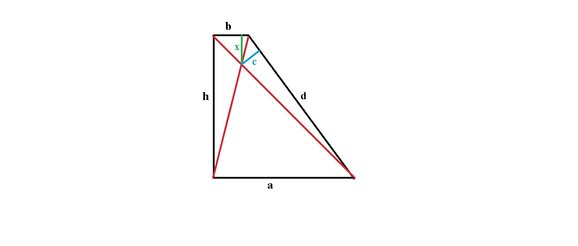
gdzie a i h wynosi po 8 cm, b = 2 cm a c = 1,3 cm.
Z powodu braku czasu zadanie rozwiązałem następnego dnia wieczorem. Okazało się, że wcześniej zadanie rozwiązała pani nauczycielka, zresztą bardzo dobrej szkoły podstawowej. Ku mojemu zdziwieniu wynik brzmiał x = 1,5 cm. Poprosiłem o rozwiązanie. Wyglądało ono mniej więcej tak:
P = 1/2 x b x h = 1/2 x 2 cm x 8 cm = 8 cm2
P - pole trójkąta o podstawie b i wysokości h
P2 = 1/2 x c x d = 1/2 x 1,3 cm x 10 cm = 6,5 cm2
P2 - pole trójkąta o podstawie d i wysokości c, d obliczone ze wzoru d2 = h2 + (a-b)2
P1 = P - P2 = 1,5 cm2
P1 - pole trójkąta o podstawie b i wysokości x
i dalej P1 = 1/2 x b x x, czyli x = 2P1/b = 1,5 cm.
Przyznam, że zadań matematycznych nie rozwiązywałem od około 20 lat. Niemniej jednak z moich obliczeń wynikało, że x = 1,6 cm. No ale wtedy c powinno być równe 1,28 cm. Kto popełnił błąd: ja, nauczycielka czy może piszący to zadanie?
PS. Z tego co się dowiedziałem w szkołach podstawowych nie uczą twierdzenia Talesa.
Inne tematy w dziale Technologie
