Motto notki: "Należy robić wszystko tak prosto, jak się da, ale nie prościej" (A. Einstein). Sprawdźmy zatem, jak prosto da się opisać ruch cząstki? I czy można to zrobić bez Transformacji Lorentza?
Część #1: https://www.salon24.pl/u/model-naturalny/678523,bedzie-sie-dzialo
(2) Mrówka relatywistyczna
Wyjaśnienie Transformacji Lorentza na podstawie ruchu mrówki
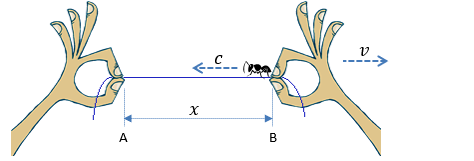
Chwyćmy w palce kawałek gumki i ustawmy na jej brzegu mrówkę (jak na poniższym rysunku).
 Rysunek 2.1
Rysunek 2.1
Nasza mrówka porusza się wolno z prędkością c ok. 299 mm/min. Dla wygody, przyjmijmy c=300 mm/min. Mrówka nigdy nie zwalnia i nie przyspiesza. Umie chodzić wyłącznie z jedną, zawsze tą samą prędkością c=const i nie ustoi w miejscu. Dodatkowo załóżmy, że mrówka w czasie podróży jest niewidoczna i możemy ją obserwować jedynie na brzegach gumki. Celowo robimy tu analogię między mrówką i fotonem, żeby łatwiej było wyjaśnić paradoksy przyświetlnych prędkości odwołując się do prostego modelu.
No dobrze, jeśli już porównaliśmy mrówkę do fotonu, to czym w tej analogii jest gumka? Gumka symbolizuje ośrodek, w którym porusza się foton. Ale przecież ośrodka dla fotonu nie widać. To dla pełnej zgodności gumka też niech będzie niewidoczna.
Obserwacja naszego doświadczenia nieco się komplikuje, ale od czego są oczy wyobraźni – musimy tylko ruch mrówki (podobnie, jak fotonu) sobie wyobrazić.
Jeśli dłonie będziemy trzymać nieruchomo w odległości x=300 mm, to możemy łatwo wyliczyć, ile czasu t zajmie mrówce przejście na drugi koniec gumki: t=c/x=1 minuta.
Ale co się stanie, jeśli nieco utrudnimy mrówce zadanie i będziemy rozciągać niewidoczną gumkę ze stałą prędkością v? Jak teraz wyliczyć czas, po którym mrówka dotrze do celu?
Zauważmy, że mrówka dobiegnie na drugi brzeg z prędkością c, bez względu na to, czy będziemy gumkę rozciągać, czy nie. Przecież tylko z taką prędkością umie się poruszać.
A zatem obserwator widzi, że mrówka staruje z prędkością c oraz dobiega do celu również z prędkością c. Ale nic nie wie o jej podróży, bo zarówno gumka, jak mrówka są w tym czasie niewidoczne. Obserwator nawet nie wie, że jest tam jakaś gumka, może mrówka porusza się po niewidocznym patyczku? Pogrążony w domysłach może zadać sobie pytanie: Jak to możliwe, że podróżująca po patyczku mrówka wystartowała z prędkością c i z taką samą prędkością c uderzyła w cel uciekający z prędkością v? A następnie zagłębi się w zaobserwowany paradoks c-v=c.
No cóż... Jeśli obserwator założył, że mrówka (wbrew temu, co wiemy) porusza się po patyczku, to doprawdy trudno zazdrościć mu ekwilibrystyki, którą musi wykonać, żeby opisać zjawisko.
Pójdźmy jego tropem. Na pierwszy problem natrafimy przykładając nasze oko wyobraźni z jednej, a następnie z drugiej strony układu. Zobaczmy oba przypadki na rysunku.
Na początek spójrzmy lewym okiem.
 Rysunek 2.2: Droga mrówki oglądana lewym okiem
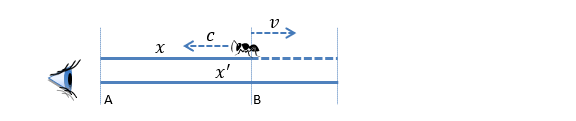
Rysunek 2.2: Droga mrówki oglądana lewym okiem
x, x' – początkowa i końcowa odległość między dłońmi,
A, B – początkowe położenie dłoni.
Widzimy zbliżającą się mrówkę, która wystartowała z odległości x. Ponieważ mrówka dotarła do obserwatora z prędkością c, to musimy uznać, że patyczek jest trzymany w lewej dłoni, a prawa odsuwa się z prędkością v. Mierząc początkową i końcową odległość między dłońmi, możemy obliczyć prędkość v, z jaką były rozsuwane.
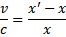 (2.1)
(2.1)
A teraz na tę samą sytuację spójrzmy prawym okiem.
 Rysunek 2.3: Droga mrówki oglądana prawym okiem
Rysunek 2.3: Droga mrówki oglądana prawym okiem
Teraz widzimy, że mrówka goni uciekającą dłoń i efekcie musi pokonać drogę x'. Mrówka startuje z prędkością c, a zatem musimy uznać, że patyczek jest trzymany w prawej dłoni, natomiast lewa oddala się z prędkością v. Obliczmy prędkość rozsuwania dłoni dla tego przypadku.
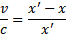 (2.2)
(2.2)
Chwileczkę… Coś się nie zgadza. Załóżmy, że rozsunęliśmy dłonie w stosunku x'/x=3/2. Otrzymamy wtedy następujące wyniki:
- Patrząc z lewej strony
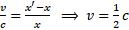
- Patrząc z prawej strony
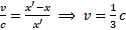
Okazuje się, że prędkości są różne. Czy to znaczy, że prawa dłoń oddala się od lewej z inną prędkością, niż lewa od prawej?
Odpowiedzią na to pytanie są wzory transformacyjne Lorentza. Wprowadzają one przekształcenia, które pozwalają uzyskać jednakową prędkość v dla obu punktów obserwacji. Jak to się dzieje?
W myśl Transformacji Lorentza prędkość mrówki c jest zawsze stała względem obserwatora, natomiast czas i długość mogą ulegać pewnym proporcjonalnym zniekształceniom. W efekcie omawiany model ruchu mrówki (po patyczku) przekształca się do poniższego schematu.
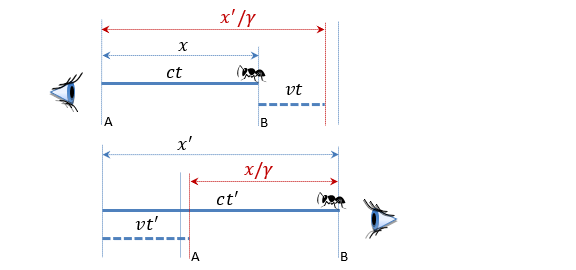 Rysunek 2.4
Rysunek 2.4
x, t – droga i czas podróży mrówki rejestrowane lewym okiem,
x', t' – droga i czas podróży mrówki rejestrowane prawym okiem,
γ – miara dokonanej korekty.
„Zasada działania” Transformacji Lorentza polega na swoistej umowie, że okiem lewym potrafimy poprawnie ocenić jedynie początkową długość patyczka, a okiem prawym jedynie końcową jego długość. Kolor czerwony dotyczy odległości, których
nie mierzymy bezpośrednio, a jedynie wyliczamy. Podkreślmy to wyraźnie – zgodnie z Transformacją Lorentza tych odległości nie mierzymy. A skoro ich nie mierzymy… O, to bardzo wygodne, ponieważ umożliwia takie umowne zdefiniowanie tych wymiarów, żeby rachunki się zgadzały. W tym przypadku dzieląc długości tych „niemierzonych” odcinków przez pewien współczynnik γ.
W Teorii Względności dokonana korekta nazywa się kontrakcją długości i mówi, że poprawnie możemy odczytać długość odcinka tylko w układzie, którym ten odcinek spoczywa (bo tylko tu możemy zweryfikować jego długość przez pomiar). W każdym innym układzie, wyliczona wartość będzie mniejsza lub co najwyżej równa, bo jest dzielona przez współczynnik γ.
Zobaczmy, jak poczynione korekty (zaznaczone na czerwono) wpływają na wynik obliczeń.
- Patrząc z lewej strony
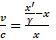
- Patrząc z prawej strony
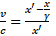
Porównując powyższe zależności możemy wyliczyć, jaki musi być współczynnik γ, żeby obydwie prędkości były sobie równe:
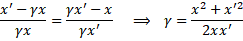 (2.3)
(2.3)
Podstawiając te same co poprzednio wartości liczbowe x'/x=3/2 uzyskujemy γ=13/12 i nareszcie zgodne prędkości.
- Patrząc z lewej strony
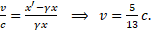
- Patrząc z prawej strony
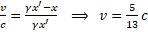
Hurra! A zatem po korekcie uzyskaliśmy takie same prędkości v rejestrowane lewym i prawym okiem. I o to właśnie chodziło w tym przekształceniu. Przekształceniu Lorentza. Wartość γ nosi nazwę współczynnika Lorentza i jest swoistą miarą dokonanej korekty.
A skoro już z sukcesem uzgodniliśmy jednakową prędkość v dla obu punktów widzenia, możemy wyliczyć jak ta prędkość wpływa choćby na czas, po jakim podróżująca (po wymyślonym patyczku) mrówka dotrze do celu. Ale o tym w następnej notce.
Część #3: https://www.salon24.pl/u/model-naturalny/1187226,predkość-lorentza
Inne tematy w dziale Technologie

